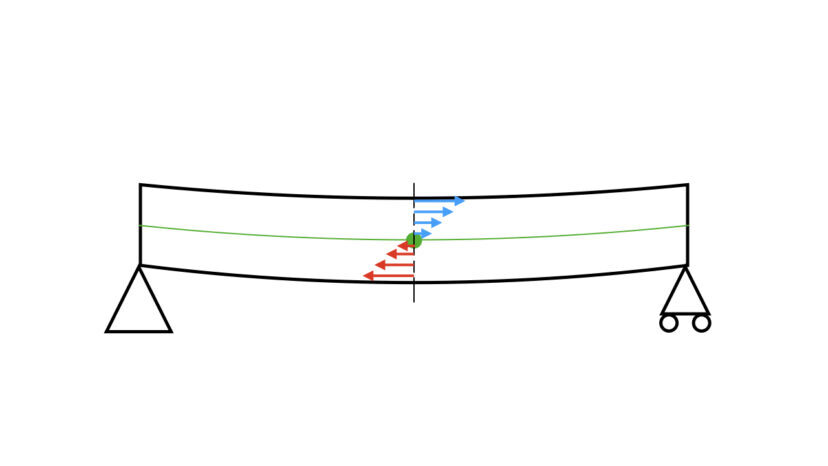
今回は、曲げ応力の式の導出についてお話しします。
曲げ応力とはどのような応力のことかを知りたい方は、こちらの記事を参考にしてみてください
まず、梁を曲げたときに生じる「ひずみ」を、「曲率」と「フックの法則」を使うことで、以下の式が導出されます。
$$\sigma = E \frac{y}{r} \cdots(1)$$
この式の導出について、詳しくは以下の記事で解説しておりますので、よかったら参考にしてみてください。
続いて「曲率半径」を、「モーメント荷重」や「断面二次モーメント」を使うことによって、以下のように表すことができます。
$$\frac{1}{r}=\frac{M}{EI}\cdots(2)$$
この式の導出について、詳しくは以下の記事で解説しておりますので、よかったら参考にしてみてください。
では、(2)式を(1)式に代入してみますと、以下のようになります。
$$\sigma = \frac{My}{I} \dots(3)$$
材料はσが最大のところが最も壊れやすいので、σが最大になる場所について考えます。
σが最大になるのは梁の中立面(中立軸)から最も離れた位置、つまりyが最大の位置ですが、これは梁の断面形状によって異なります。
例えば、
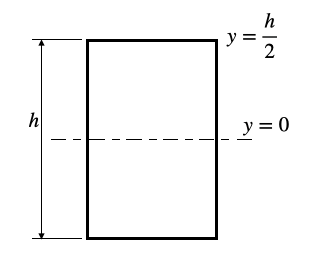
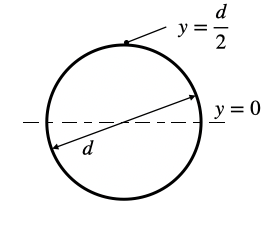
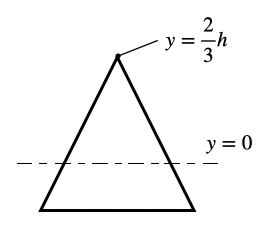
となります。(なお、y=0は断面の図心の位置です)
そして断面二次モーメントの値もまた、梁の断面形状によって決まる値です。
そこで、Zという文字を用意して、梁の断面形状によって決まるものをまとめると、以下の通りとなります。
$$Z=\frac{I}{y}$$
このZのことを、断面係数と呼びます。
よって、曲げ応力の計算式は、以下のとおりとなります。
$$\sigma = \frac{M}{Z} \dots(4)$$
ちなみに、断面係数Zは「梁の断面形状によって決まる値」といいましたが、代表例を挙げると以下の通りとなります。
 |
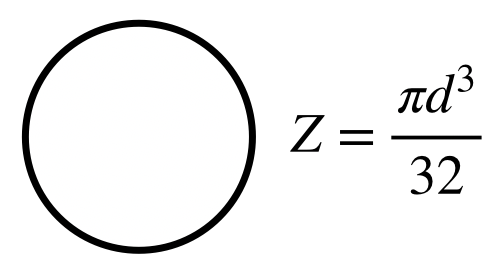 |
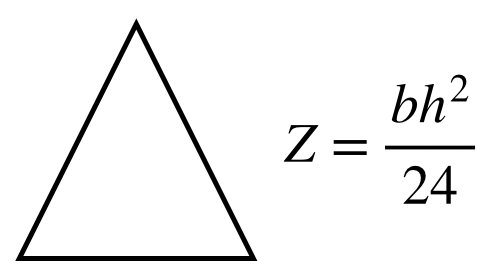 |
その他、さまざまな断面形状については、以下のページに公式集・計算ツールを掲載しております。
曲げ応力の導出は、長い道のりですが、(4)式の丸暗記をするのではなく、その経緯まで知っておくと、実際のものに起こっている現象がイメージできて、応用を効かせることができます。
ちなみに、以下のページに計算ツールをご用意しているので、よろしければご活用ください。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

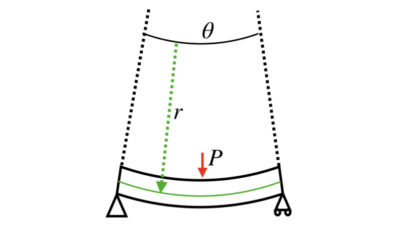
曲げモーメントから読み解く、梁の曲率半径の導出
材料力学 演習問題 05【曲げ応力】
