こんにちはー、りびぃです。
普段はFA(ファクトリー・オートメーション)の業界で設計をしている現役のエンジニアです。
設計業務においては、そのケースに応じた強度・応力の計算を行いますが、まれに曲面・球面に発生する応力について計算する必要があるケースもあります。
例えば、平板の圧延とか、台車の車輪に関する応力を求めたいときなどですね−
![]()
応力の計算といえばざっくりいうと「その場所発生する力を、受ける面積で割って求める」のですが、この対象物が曲面や球面に発生するとなると、途端に難しくなります。
というのも、曲面や球面を剛体(変形を考慮しない)として考えると、
あれ・・・?受ける面積っていっても、曲面や球面だと線接触・点接触になるのでは?
となって、受ける面積を求めることができないのです。
実際の現象では、接触する際にはそれぞれの物体が変形をしますし、その接触部は面になっているのですが、その接触面や応力についてどう考えればよいかというのは難しい問題です。
そこで役立つのが「ヘルツの接触応力」の公式になります。
ヘルツの接触応力とは、曲面や球面をもつ物体の接触部にかかる応力や圧力のことを言います。
ただ実際ネット等で調べてみても数式がズラーっと並んでいるものが多いため
自分が計算したいケースにも使える式なのか、よくわからんなぁ・・・
と不安になりますよねー
そこで今回は、このヘルツの接触応力の公式のなかで、特に使われるケースについて、わかりやすく解説をしていきます。
目次
公式を紹介する前に、まずはどのような前提で使える公式なのかについて抑えておきましょう。
前提が間違っていると、理論と実際の現象とのズレが大きくなるからねー!
前提は以下のとおりです。
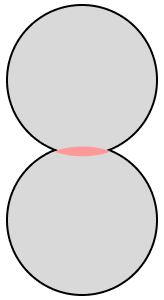
まずは球面と球面との接触のケースについて見ていきましょう。
詳細は省略しますが、このケースにおける接触面半径$a$,両球の接近量$\delta$、接触圧力$p$、最大接触圧力$p_{max}$は次の公式にて求められることが知られています。
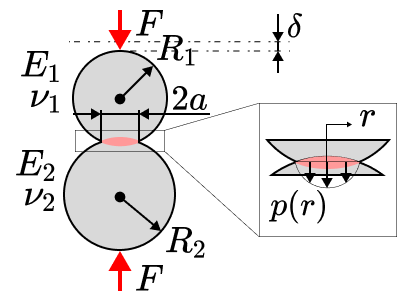
$$\displaystyle a =\sqrt[3]{ \frac{3F}{4} \frac{R_e}{E_e}} $$
$$\displaystyle \delta =\sqrt[3]{ \frac{9F^2}{16R_eE_e^2}} $$
$$\displaystyle p(r)= \frac{3}{2\pi a^2}\sqrt{1-\left(\frac{r}{a}\right)^2}$$
$$\displaystyle p_{max}=\frac{3F}{2\pi a^2}$$
ここで、
となります。
球面の接触の場合、接触部の面は円または楕円になります。
ここでいう最大面圧っていうのは、球に発生する応力の最大値って考えていいの?
と思いがちですが、実は違います。
最大接触面圧というのは「接触部において発生する圧力の最大値こと」を言います。
主に表面の摩耗や塑性変形に関する評価に使用します。
一方で応力は「材料内部で発生する応力の最大値のこと」を言います。
例えば脆性材料においては、特定の応力を超えるとクラックが発生したりするので、その評価に使用します。
の場合(鉄などがポアソン比0.3程度)において最大引張応力が発生する場所は接触部の縁のところ、最大せん断応力は、接触面の中央部でかつ深さ$z=0.47a$の場所であり、それぞれの値は
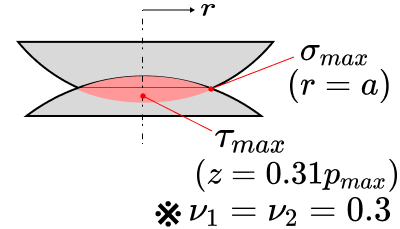
$$\displaystyle \sigma_{max}=\frac {1-2\nu}{3}p_{max}$$
$$\displaystyle \tau_{max}=0.31p_{max}$$
となります(せん断応力は、ポアソン比0.3の場合の値となります)。
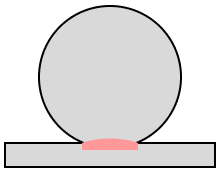
続いては、片方が平面の場合について見ていきましょう。
「平面」というのは言い換えると「曲率半径が無限大」ということになります。
ということで、$R_2 \rightarrow \infty$となることから、
$$\displaystyle \frac{1}{R_e} = \frac{1}{R_1} + \frac{1}{\infty} \simeq \frac{1}{R_1}$$
という近似が得られます。
よってこのケースにおける接触面半径$a$,両球の接近量$\delta$、接触圧力$p$、最大接触圧力$p_{max}$は次の公式のようになります。
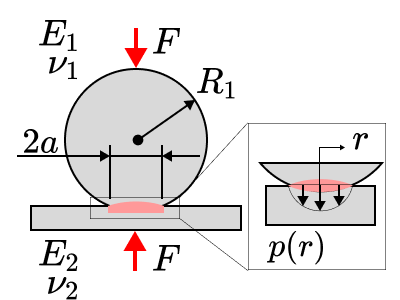
$$\displaystyle a =\sqrt[3]{ \frac{3F}{4} \frac{R_1}{E_e}} $$
$$\displaystyle \delta =\sqrt[3]{ \frac{9F^2}{16R_1E_e^2}} $$
$$\displaystyle p(r)= \frac{3}{2\pi a^2}\sqrt{1-\left(\frac{r}{a}\right)^2}$$
$$\displaystyle p_{max}=\frac{3F}{2\pi a^2}$$
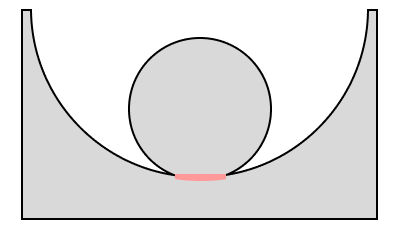
続いては、片方が凹面の場合について見ていきましょう。
ベアリングの玉と外輪との関係とかに使えそうだね!
凹面の場合、半径はマイナスの値として代入をするのがポイントとなります。
つまり
$$\displaystyle \frac{1}{R_e}=\frac{1}{R_1}+\frac{1}{-R_2}$$
となります。
その他は凸面と凸面の場合と同じであり接触面半径$a$,両球の接近量$\delta$、接触圧力$p$、最大接触圧力$p_{max}$は次の公式のようになります。
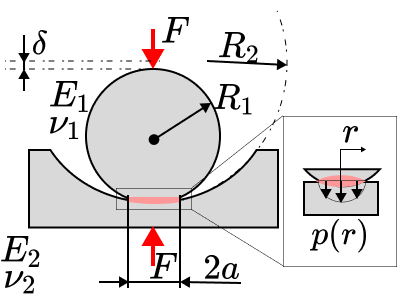
$$\displaystyle a =\sqrt[3]{ \frac{3F}{4} \frac{R_e}{E_e}} $$
$$\displaystyle \delta =\sqrt[3]{ \frac{9F^2}{16R_eE_e^2}} $$
$$\displaystyle p(r)= \frac{3}{2\pi a^2}\sqrt{1-\left(\frac{r}{a}\right)^2}$$
$$\displaystyle p_{max}=\frac{3F}{2\pi a^2}$$
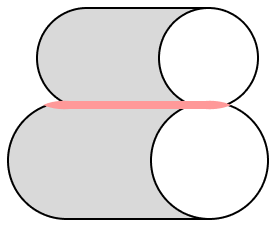
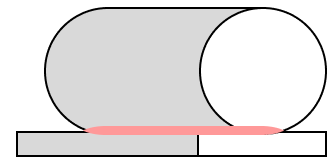
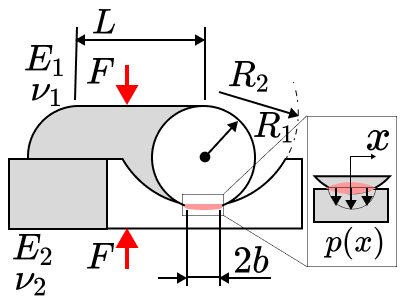
続いては円筒面のなかでも凸面同士の場合について見ていきたいと思います。
円筒面の場合、接触部の面は帯状になります。
この時、接触面半幅$b$,接触圧力$p$、最大接触圧力$p_{max}$は次の公式のようになります。
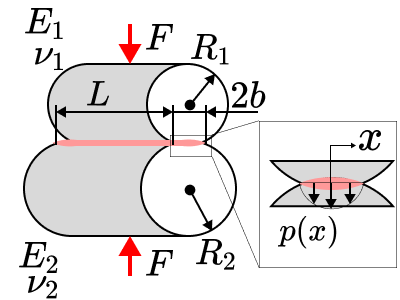
$$\displaystyle b=\sqrt{\frac{4FR_e}{\pi E_eL}}$$
$$\displaystyle p(x)=\frac{2F}{\pi bL}\sqrt{1-\left(\frac{x}{b}\right)^2}$$
$$\displaystyle p_{max}= \frac{2F}{\pi bL}$$
円筒面の場合、両球の接近量$\delta$はヘルツの公式からは求めることができないとのことなので、ここでは割愛します。
続いて円筒面で片方が平面の場合についての式を紹介します。
こちらも「平面=曲率半径が無限大」と読み替えればよいので、
$$\displaystyle = \frac{1}{R_1}+\frac{1}{\infty}\simeq \frac{1}{R_1}$$
となります。
よって、接触面半幅$b$,接触圧力$p$、最大接触圧力$p_{max}$は次の公式のようになります。
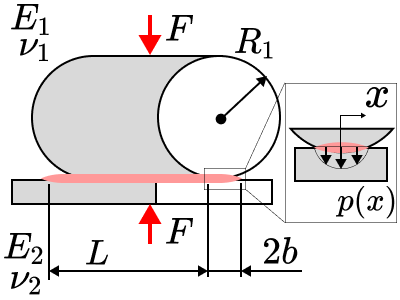
$$\displaystyle b=\sqrt{\frac{4FR_e}{\pi E_eL}}$$
$$\displaystyle p(x)=\frac{2F}{\pi bL}\sqrt{1-\left(\frac{x}{b}\right)^2}$$
$$\displaystyle p_{max}= \frac{2F}{\pi bL}$$
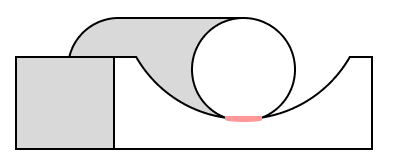
最後に円筒面の場合で、片方が凹面の場合について紹介します。
凹面の場合には曲率半径をマイナスの値とすればよいので、
$$\displaystyle \frac{1}{R_e}=\frac{1}{R_1}+\frac{1}{-R_2}$$
となります。
よって、接触面半幅$b$,接触圧力$p$、最大接触圧力$p_{max}$は次の公式のようになります。
$$\displaystyle b=\sqrt{\frac{4FR_e}{\pi E_eL}}$$
$$\displaystyle p(x)=\frac{2F}{\pi bL}\sqrt{1-\left(\frac{x}{b}\right)^2}$$
$$\displaystyle p_{max}= \frac{2F}{\pi bL}$$
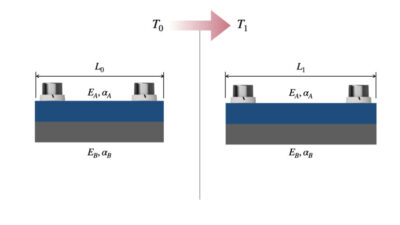
2つの平板間の熱応力の計算方法