
こんにちはー、リヴィです!私は普段、機械を設計する仕事をしています。
機械の設計では様々な計算をしながら検討を進め、図面を書いていくという流れで進められますが、
色んな計算の中で、特にマスターしておきたいものの一つが「トルク」となります。
トルクとは一言でいうと「回転力」の事を言うのですが、トルクは機械の設計計算において、
と言った感じで、とにかくあらゆる場面でに利用されるものになります。
工学の勉強をしたことがある人であれば「トルク」という言葉を聞いたことぐらいはあると思いますが、いざ「トルクの観点から設計検討してください」と指示されてみると・・・
あれ、どうすりゃいいんだっけ・・・?自分、何となくしか理解していないじゃん・・・
ってなりがちです。
またトルクの計算は、機械の設計の根幹になることもよくあるので、トルクについて正しく理解できていなかったり、計算を間違えたりすると、最初からやり直さなければならないレベルになります。
そこで、この記事では「トルク」についての基礎や計算の手順などについて詳しく解説をいたします。
トルクの計算式は2パターンあります。
それぞれ、状況に応じて式を使い分ける必要がありますので、両方とも理解するようにしましょう。
「回転力」と「力」の関係について見る時の計算式は以下のとおりです。
$$T = F\cdot L\cdots(1-1)$$
| $$T$$ | トルク$\rm{[N\cdot m]}$ |
| $$F$$ | 力$\rm{[N]}$ |
| $$L$$ | 長さ$\rm{[m]}$ |
なんとなく、学校で習ったことある−!
という方もいらっしゃるかと思います。これはいわゆる「テコの原理」の式です。
では、どのようにしてこの式を使うかについて、例題を見てみましょう。
例えば、ドアノブを手で回す状況について考えてみましょう。
ドアノブの中には「バネ」が入っているので、力を加えていないと元の位置に戻ってしまいます。
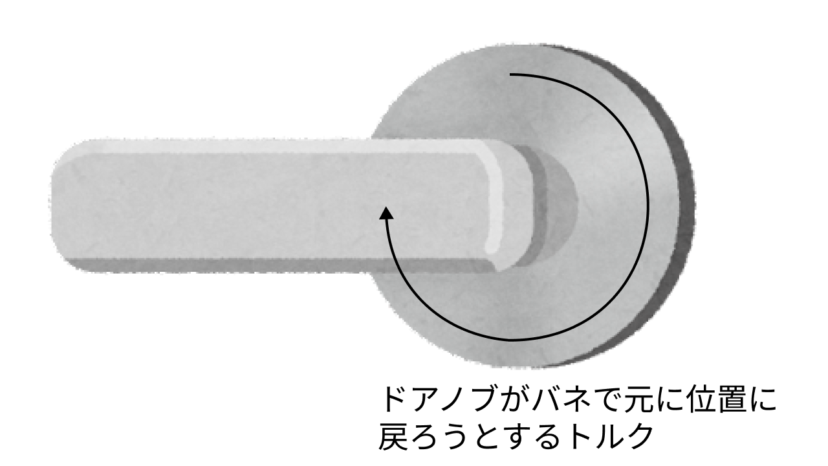
ですから、ドアノブを回すためには「ドアノブが元の位置に戻ろうとする時のトルク」より大きいトルクをかける必要があります。
ここで、「あなたがドアノブのレバーにかける力」を$F$、「ドアノブのレバーの長さ」を$L$とすると、「あなたがドアノブのレバーに力をかけたことによって発生するトルク」$T$は以下の通りとなります。
$$T = F\cdot L \cdots(1-2)$$
その上で、「ドアノブが元の位置に戻ろうとする時のトルク」を$T_D$とすると、ドアノブを回すためには$T_D<T$が成り立つ必要があります。
この式を利用すると、$(1-2)$式は次のように書き換えることができます。
$$T_D<F\cdot L\cdots(1-3)$$
この式から「ドアノブを回すためには、レバーにかける力はどれぐらい必要か?」というのは、
$$\displaystyle F>\frac{T_D}{L}\cdots(1-4)$$
という形で求めることができます。
このような感じで、トルクの式を利用していきます。
「駆動源を使って物体を回転させるとき」などのように、「回転するもの・されるもの」の関係の場合には、回転の運動方程式からトルクを求める必要があります。
モータやエンジンによって回転力を入力する場合などですねー
回転の運動方程式は、以下の式で与えられます。
$$T=J\frac{\omega_2-\omega_1}{\Delta t}\cdots(2-1)$$
| $$T$$ | トルク$\rm{[N\cdot m]}$ |
| $$J$$ | 慣性モーメント(イナーシャ)$\rm{[kg\cdot m^2]}$ |
| $$\omega_1$$ | 変化前の角速度$\rm{[rad/s]}$ |
| $$\omega_2$$ | 変化後の角速度$\rm{[rad/s]}$ |
| $$\Delta t$$ | 加減速時間$\rm[s]$ |
あるいは、
$$T=J\frac{2\pi(N_2-N_1)}{60\Delta t}\cdots(2-2)$$
| $$T$$ | トルク$\rm{[N\cdot m]}$ |
| $$J$$ | 慣性モーメント(イナーシャ)$\rm{[kg\cdot m^2]}$ |
| $$N_1$$ | 変化前の回転数$\rm{[rpm]}$ |
| $$N_2$$ | 変化後の回転数$\rm{[rpm]}$ |
| $$\Delta t$$ | 加減速時間$\rm[s]$ |
物理の教科書など、学術的な資料ですと$(2-1)$が、機械設計の分野ですと$(2-2)$が使われることが一般的ですねー。なので機械設計の皆さんは$(2-2)$を使いましょう。
この回転の運動方程式については見慣れていない方がいるかと思いますので、式の意味について軽く説明すると、
となります。
慣性モーメントは、簡易的な計算モデルであれば、エクセルやこちらの「慣性モーメント 計算ツール」を使って算出することができます。
ですが実際の設計においては、簡易的な計算モデルで求められるケースの方がレアですので、3DCADの中のコマンドを使って求めることが一般的です。 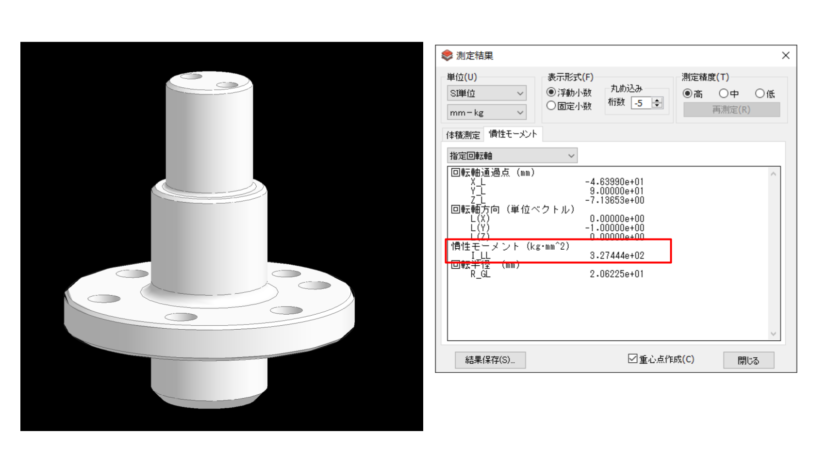
続いて回転数(角速度)についてですが、機械設計で一番計算するのが多いのが、
の2パターンとなります。
これらの数値や状況を踏まえて$(2-1)$を使ってトルクを計算し、それをモーターメーカのカタログを見ながら「計算したトルク以上にトルクを発生させられるモータ」を探して選定するという流れになっていきます。
ただ、実際のモータの選定時は「トルクさえOKなら問題なし!」ではなく、他にもいくつか計算が必要ですからねー
「力」と「回転力」の関係についてのトルク計算は
$$T = F\cdot L\cdots(1-1)$$
で求められますが、この式を使う上での注意があります。
それは「力Fは、Lの方向と直角に交わる分の値だけ含めること」です。
例えば、ドアノブのレバーに対して垂直に力をかけるときは$(1-1)$でOKなのですが、
力のかけ方が斜めになっている場合は、ドアノブのレバーの方向と直角に交わる分の値だけになるよう、$(1-5)$のように三角関数を使った式で計算する必要があります。
$$T = F\sin\theta\cdot L\cdots(1-5)$$
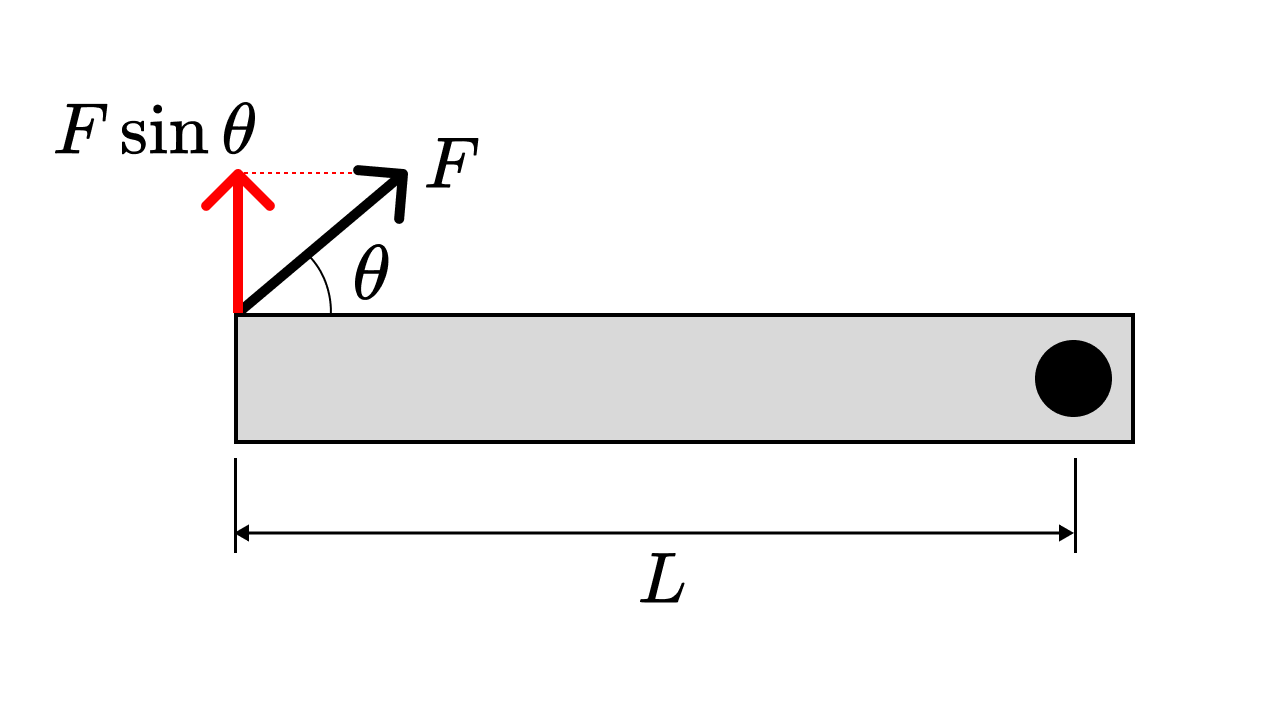
ちなみに「レバーと同じ方向に押したり引いたりする場合」はトルクが0、つまり「どれだけ一生懸命力を加えても、ドアノブは回らない」となります。
「時間の話が含まれる場合」の計算で注意しなければならないのは「どこの軸についての計算をしているか?」になります。
「どこの軸・・・」ってことは、軸って複数あるの?
と思ったあなた・・・!、勘が鋭いです笑!
機械の設計では「モータ」と「回したい部品」の2つ意外にも、
などという、モータの動力を中継する部品を利用します。

これらの部品から見た時、
といったように、軸の場所には名前がついています。
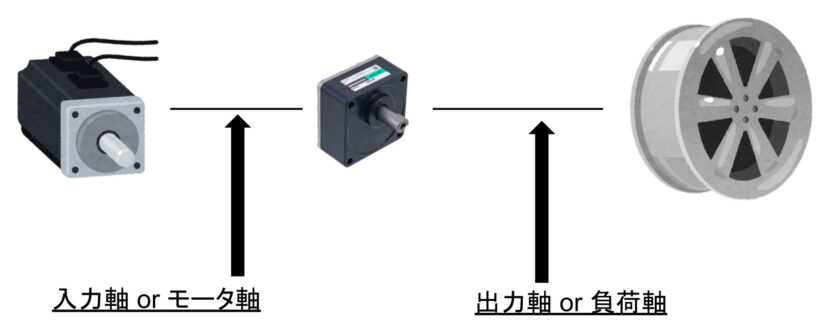
なので「複数の軸」というのはこの2つの軸のことであり、そのうち「どちら側で計算をしているか?」によってトルクの計算方法が変わります。
これには、モータの動力を中継する部品の「減速比」呼ばれる、負荷トルク(回転させるのに必要なトルク)を減少させるパラメータが関係しています。
「減速比」を言葉通りに捉えると「減速させて何の意味があるの?」と混乱しがちですが、「負荷トルクを減少させるのが狙い」という場合がほとんどですー。
以上を踏まえると、どちら側の軸で計算をするかによって、トルクの計算式は以下の通りになります。
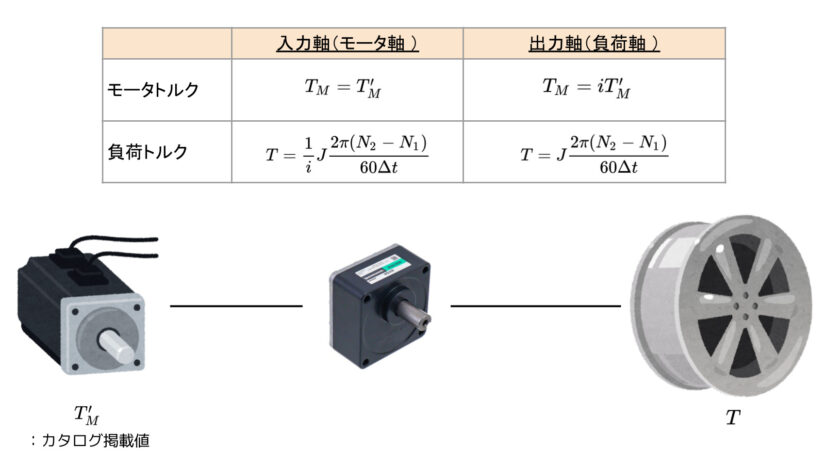
では、これらについて解説していきます。
モータ軸上での負荷トルクの計算式は、以下の通りとなります。
$$\displaystyle T = \frac{1}{i}\cdot J\frac {2\pi(N_2-N_1)}{60\Delta t}\cdots (2-3)$$
| $$T$$ | トルク$\rm{[N\cdot m]}$ |
| $$i$$ | 減速比$\rm{[-]}$ |
| $$J$$ | 慣性モーメント(イナーシャ)$\rm{[kg\cdot m^2]}$ |
| $$N_1$$ | 変化前の回転数$\rm{[rpm]}$ |
| $$N_2$$ | 変化後の回転数$\rm{[rpm]}$ |
| $$\Delta t$$ | 加減速時間$\rm[s]$ |
例えば、減速比が2であるギアヘッドを導入すれば、回したい部品の必要トルクは2分の1になります。
この数値を満たせるようなモータを、カタログから選定するという流れになります。
負荷軸上でのトルクを計算する場合は$(2-1)$をそのまま使います。
$$\displaystyle T = J\frac {2\pi(N_2-N_1)}{60 \Delta t}\cdots (2-1)$$
これに対して、モータが発生させられるトルクの能力との比較をするわけですが、このとき、
$$\displaystyle T_M = i\cdot T_M’\cdots(2-6)$$
| $$T_M$$ | 修正後のモータトルク$\rm{[N\cdot m]}$ |
| $$i$$ | 減速比$\rm{[-]}$ |
| $$T_M”$$ | カタログ値のモータトルク$\rm{[N\cdot m]}$ |
と言った感じに、モータの数値を修正して扱います。
ただ、わざわざカタログの数値を修正して・・・という工程が面倒くさいので、機械設計ではモータ軸上でトルクを計算するケースがほとんどですねー
ですが「モータとギアヘッドのセット品」の商品の場合、カタログに掲載されているモータトルクが「ギアヘッドの出力軸での値」であることも多いので、
カタログを見るときには注意するようにしましょう。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

機械設計の考え方【力学的に最適な設計=最良の設計ではありません】
