| 動的効果係数(ねじり) (計算ツール下部参照) |
$$k_t$$ | ||
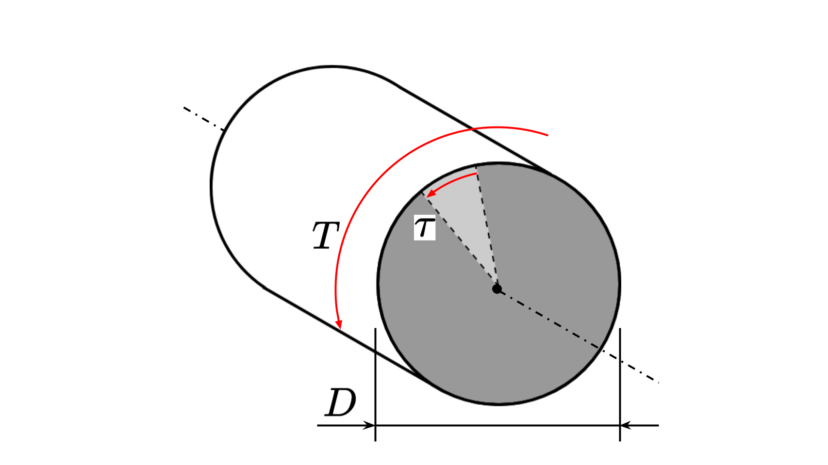
| トルク | $$T$$ | ||
| 許容ねじりせん断応力 | $$\tau$$ |
| 所要軸直径 | $$D=\sqrt[3]{\frac{16k_tT}{\pi \tau}}$$ |
| 負荷条件 | 回転軸 | 静止軸 |
|---|---|---|
| kt | ||
| 時間的にほとんど変動しない荷重(静荷重) | 1.0 | 1.0 |
| 時間的に変動する荷重(動荷重) 軽い衝撃荷重 |
1.0 ~ 1.5 | 1.5 ~ 2.0 |
| 激しい衝撃荷重 | 1.5 ~ 3.0 | |
| 動的効果係数(曲げ) (計算ツール下部参照) |
$$k_m$$ | ||
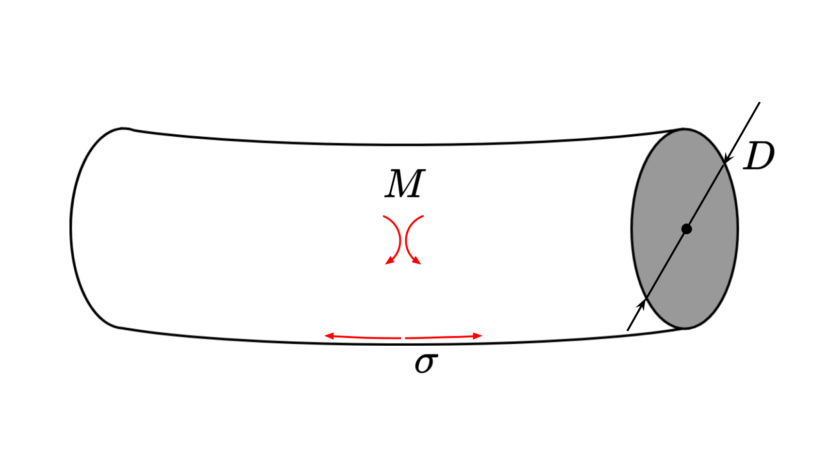
| 曲げモーメント | $$M$$ | ||
| 許容曲げ応力 | $$\sigma$$ |
| 所要軸直径 | $$D=\sqrt[3]{\frac{32k_mM}{\pi \sigma}}$$ |
| 負荷条件 | 回転軸 | 静止軸 |
|---|---|---|
| km | ||
| 時間的にほとんど変動しない荷重(静荷重) | 1.5 | 1.0 |
| 時間的に変動する荷重(動荷重) 軽い衝撃荷重 |
1.5 ~ 2.0 | 1.5 ~ 2.0 |
| 激しい衝撃荷重 | 2.0 ~ 3.0 | |
モーメントの計算は以下のツールをご活用ください。
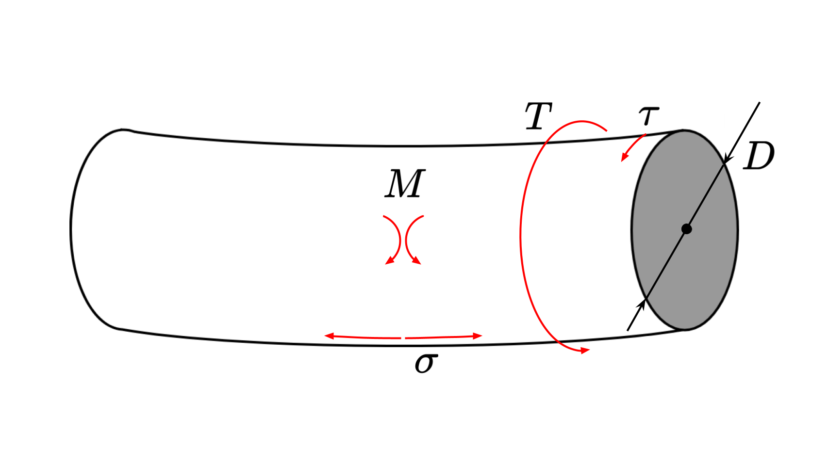
| 動的効果係数(ねじり) (計算ツール下部参照) |
$$k_t$$ | ||
| 動的効果係数(曲げ) (計算ツール下部参照) |
$$k_m$$ | ||
| ねじりトルク | $$T$$ | ||
| 曲げモーメント | $$M$$ | ||
| 許容ねじりせん断応力 | $$\tau$$ | ||
| 許容曲げ応力 | $$\sigma$$ |
| 相当ねじりトルク | $$T_e=\sqrt{M^2+T^2}$$ | ||
| 相当曲げモーメント | $$M_e=\frac{1}{2}(M+T_e)$$ | ||
| ねじりトルク視点での所要軸直径 | $$D_1=\sqrt[3]{\frac{16k_tT_e}{\pi \tau}}$$ | ||
| 曲げモーメント視点での所要軸直径 | $$D_2= \sqrt[3]{\frac{32k_mM_e}{\pi \sigma}}$$ | ||
| 所要軸直径 | $$D=\max{(D_1,D_2)}$$ |
| 負荷条件 | 回転軸 | 静止軸 | ||
|---|---|---|---|---|
| kt | km | kt | km | |
| 時間的にほとんど変動しない荷重(静荷重) | 1.0 | 1.5 | 1.0 | 1.0 |
| 時間的に変動する荷重(動荷重) 軽い衝撃荷重 |
1.0 ~ 1.5 | 1.5 ~ 2.0 | 1.5 ~ 2.0 | 1.5 ~ 2.0 |
| 激しい衝撃荷重 | 1.5 ~ 3.0 | 2.0 ~ 3.0 | ||
モーメントの計算は以下のツールをご活用ください。
| 一般伝動軸 | 等分布荷重 | δ ≦ 0.3 mm/m |
|---|---|---|
| 中央集中荷重 | δ ≦ 0.33 mm/m | |
| タービン軸 | 円筒形 | δ ≦ 0.026 ~ 0.128 mm/m |
| 円板形 | δ ≦ 0.128 ~ 0.165 mm/m | |
| 歯車をもつ伝動軸 | 最大たわみ角 i ≦ 0.001 rad (0.057 °) | |
| 普通静荷重軸 | θ < 0.33°/m |
|---|---|
| 変動荷重を受ける軸・伝動軸 | 0 < 0.25°/m |
| 急激な繰返し荷重・長い送り軸 | 0 < 0.17°/m |
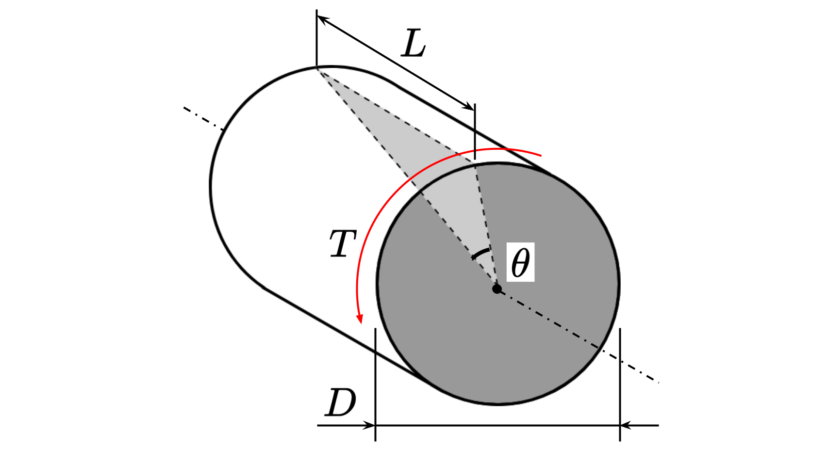
| 直径 | $$D$$ | ||
| 動的効果係数(ねじり) (計算ツール下部参照) |
$$k_t$$ | ||
| トルク | $$T$$ | ||
| 長さ | $$L$$ | ||
| 横断面係数 | $$G$$ |
| 断面二次極モーメント | $$I_p=\frac{\pi D^4}{32}$$ | ||
| 極断面係数 | $$Z_p=\frac{\pi D^3}{16}$$ | ||
| 最大ねじり応力 | $$\tau=\frac{k_tT}{Z_p}$$ | ||
| ねじれ角 | $$\theta=\frac{k_tTL}{I_pG}$$ |
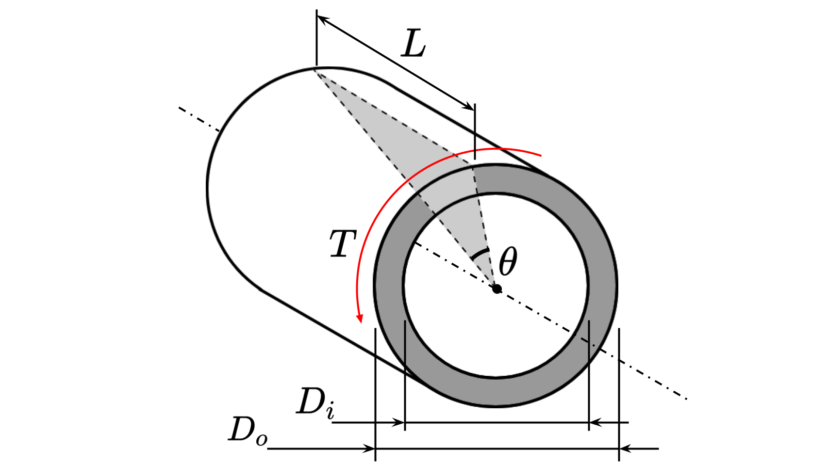
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
|
| 動的効果係数(ねじり) (計算ツール下部参照) |
$$k_t$$ | ||
| トルク | $$T$$ | ||
| 長さ | $$L$$ | ||
| 横断面係数 | $$G$$ |
| 断面二次極モーメント | $$I_p=\frac{\pi}{32}(D_o^4-D_i^4)$$ | ||
| 極断面係数 | $$Z_p=\frac{\pi}{16D_o}(D_o^4-D_i^4)$$ | ||
| 最大ねじり応力 | $$\tau=\frac{k_tT}{Z_p}$$ | ||
| ねじれ角 | $$\theta=\frac{k_tTL}{I_pG}$$ |
| 負荷条件 | 回転軸 | 静止軸 |
|---|---|---|
| kt | ||
| 時間的にほとんど変動しない荷重(静荷重) | 1.0 | 1.0 |
| 時間的に変動する荷重(動荷重) 軽い衝撃荷重 |
1.0 ~ 1.5 | 1.5 ~ 2.0 |
| 激しい衝撃荷重 | 1.5 ~ 3.0 | |

| 直径 | $$D$$ | ||
| 動的効果係数(曲げ) (計算ツール下部参照) |
$$k_m$$ | ||
| モーメント | $$M$$ |
| 断面係数 | $$Z=\frac{\pi D^3}{32}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{k_mM}{Z}$$ |
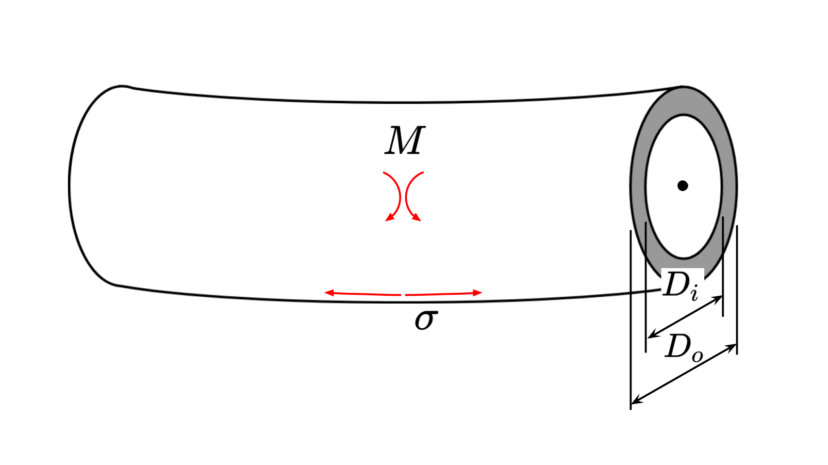
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
|
| 動的効果係数(曲げ) (計算ツール下部参照) |
$$k_m$$ | ||
| 曲げモーメント | $$M$$ |
| 断面係数 | $$Z=\frac{\pi}{32D_o}(D_o^4-D_i^4)$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{k_mM}{Z}$$ |
| 負荷条件 | 回転軸 | 静止軸 |
|---|---|---|
| km | ||
| 時間的にほとんど変動しない荷重(静荷重) | 1.5 | 1.0 |
| 時間的に変動する荷重(動荷重) 軽い衝撃荷重 |
1.5 ~ 2.0 | 1.5 ~ 2.0 |
| 激しい衝撃荷重 | 2.0 ~ 3.0 | |
モーメントの計算は以下のツールをご活用ください。

| 直径 | $$D$$ | ||
| 動的効果係数(ねじり) (計算ツール下部参照) |
$$k_t$$ | ||
| 動的効果係数(曲げ) (計算ツール下部参照) |
$$k_m$$ | ||
| ねじりトルク | $$T$$ | ||
| 曲げモーメント | $$M$$ |
| 相当ねじりトルク | $$T_e=\sqrt{M^2+T^2}$$ | ||
| 相当曲げモーメント | $$M_e=\frac{1}{2}(M+T_e)$$ | ||
| 極断面係数 | $$Z_p=\frac{\pi D^3}{16}$$ | ||
| 断面係数 | $$Z=\frac{\pi D^3}{32}$$ | ||
| 最大ねじりせん断応力 | $$\tau=\frac{k_tT_e}{Z_p}$$ | ||
| 最大曲げ応力 | $$\sigma= \frac{k_mM_e}{Z}$$ |
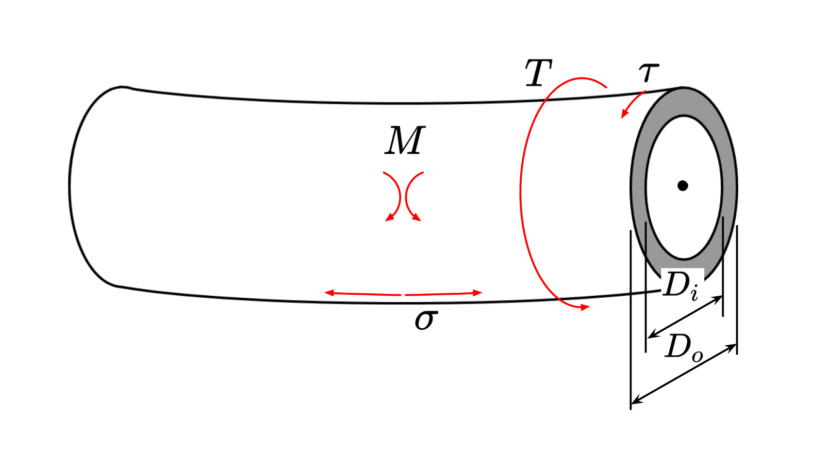
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
|
| 動的効果係数(ねじり) (計算ツール下部参照) |
$$k_t$$ | ||
| 動的効果係数(曲げ) (計算ツール下部参照) |
$$k_m$$ | ||
| ねじりトルク | $$T$$ | ||
| 曲げモーメント | $$M$$ |
| 相当ねじりトルク | $$T_e=\sqrt{M^2+T^2}$$ | ||
| 相当曲げモーメント | $$M_e=\frac{1}{2}(M+T_e)$$ | ||
| 極断面係数 | $$Z_p=\frac{\pi}{16D_o}(D_o^4-D_i^4)$$ | ||
| 断面係数 | $$Z=\frac{\pi (D_o^4-D_i^4)}{32D_o}$$ | ||
| 最大ねじりせん断応力 | $$\tau=\frac{k_tT_e}{Z_p}$$ | ||
| 最大曲げ応力 | $$\sigma= \frac{k_mM_e}{Z}$$ |
| 負荷条件 | 回転軸 | 静止軸 | ||
|---|---|---|---|---|
| kt | km | kt | km | |
| 時間的にほとんど変動しない荷重(静荷重) | 1.0 | 1.5 | 1.0 | 1.0 |
| 時間的に変動する荷重(動荷重) 軽い衝撃荷重 |
1.0 ~ 1.5 | 1.5 ~ 2.0 | 1.5 ~ 2.0 | 1.5 ~ 2.0 |
| 激しい衝撃荷重 | 1.5 ~ 3.0 | 2.0 ~ 3.0 | ||
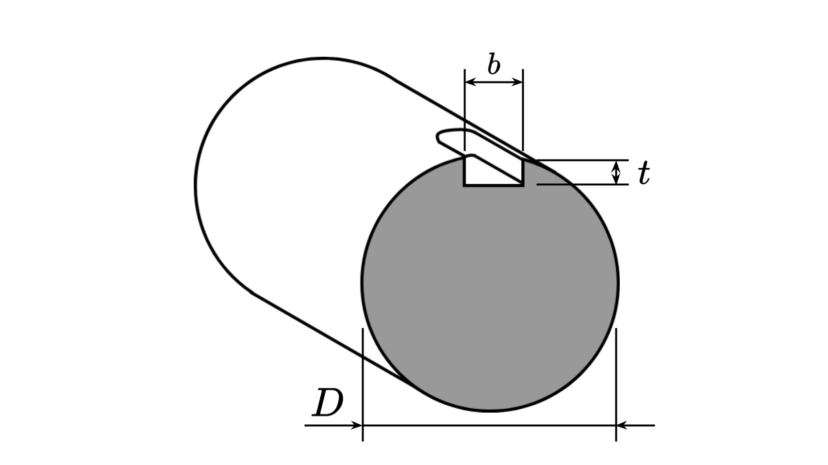
| 直径 | $$D$$ | ||
| キーの幅 | $$b$$ | ||
| キー溝の深さ | $$t$$ |
| キー溝なし軸ねじり応力に対するキー溝あり軸ねじり応力の比 (ムーアの実験式) |
$$e=\frac{\tau'}{\tau}=1.0-0.2\frac{b}{D}-1.1\frac{t}{D}$$ |
キー・キー溝の寸法表は以下のページをご参照ください。
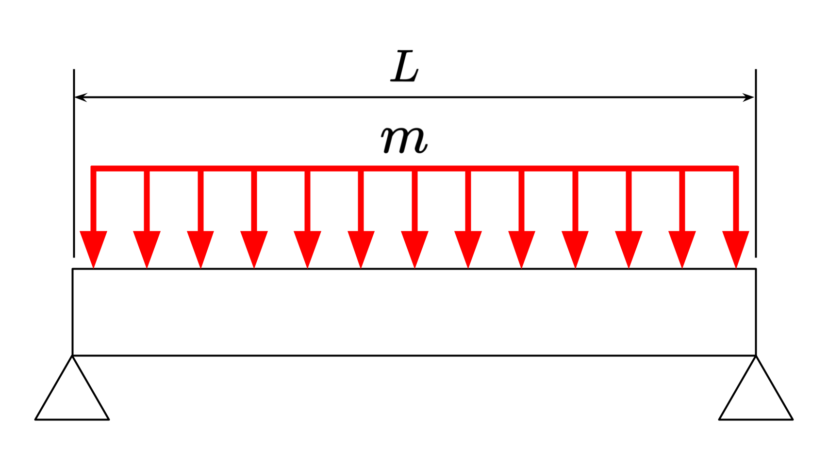
| 直径 | $$D$$ | ||
| ヤング率 | $$E$$ | ||
| 負荷質量 | $$m$$ | ||
| 長さ | $$L$$ |
| 断面二次モーメント | $$I=\frac{\pi D^4}{64}$$ | ||
| 危険速度 | $$\omega_c=\sqrt{\frac{97.4EI}{mL^3}}$$ |
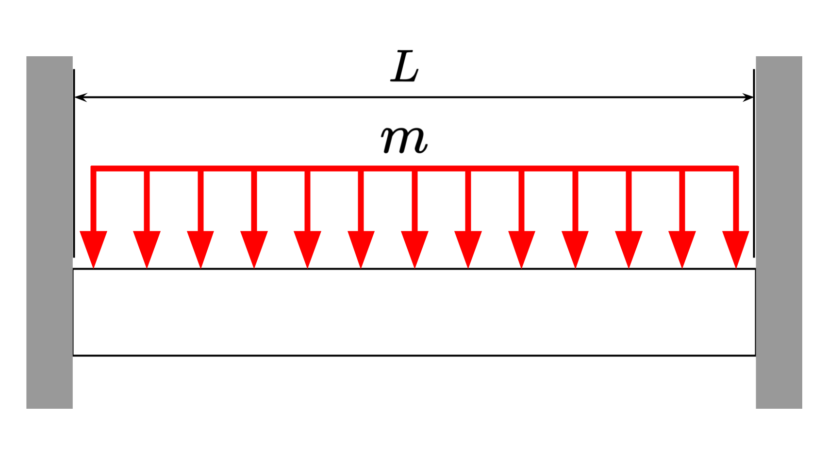
| 直径 | $$D$$ | ||
| ヤング率 | $$E$$ | ||
| 負荷質量 | $$m$$ | ||
| 長さ | $$L$$ |
| 断面二次モーメント | $$I=\frac{\pi D^4}{64}$$ | ||
| 危険速度 | $$\omega_c=\sqrt{\frac{50EI}{mL^3}}$$ |
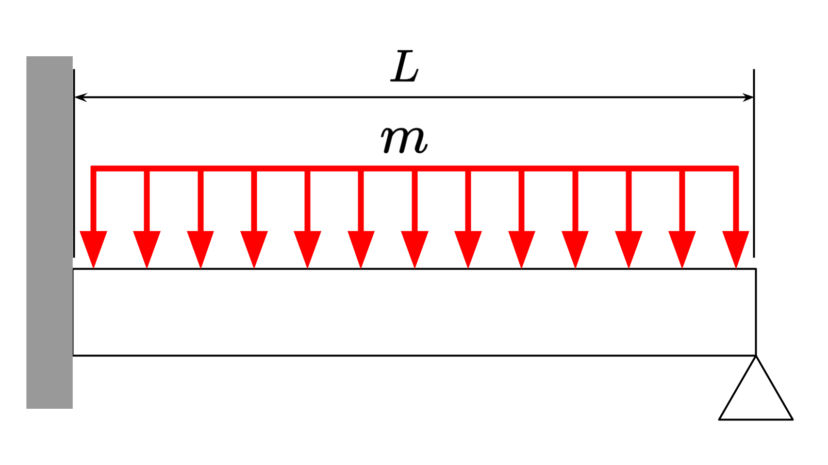
| 直径 | $$D$$ | ||
| ヤング率 | $$E$$ | ||
| 負荷質量 | $$m$$ | ||
| 長さ | $$L$$ |
| 断面二次モーメント | $$I=\frac{\pi D^4}{64}$$ | ||
| 危険速度 | $$\omega_c=\sqrt{\frac{238EI}{mL^3}}$$ |
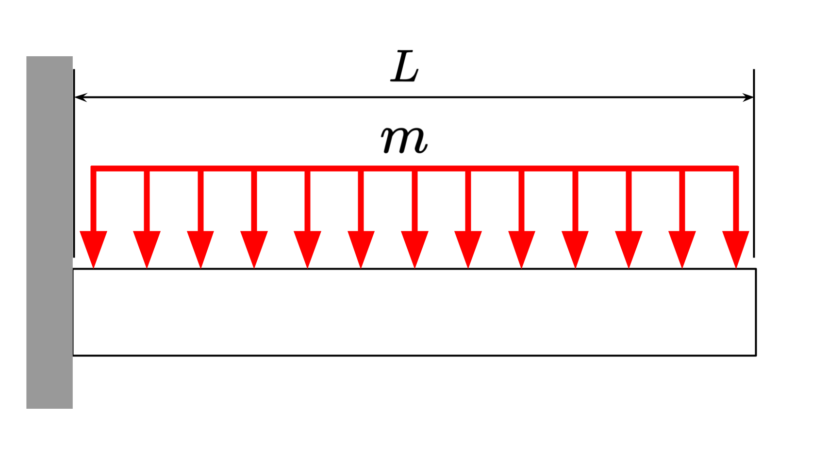
| 直径 | $$D$$ | ||
| ヤング率 | $$E$$ | ||
| 負荷質量 | $$m$$ | ||
| 長さ | $$L$$ |
| 断面二次モーメント | $$I=\frac{\pi D^4}{64}$$ | ||
| 危険速度 | $$\omega_c=\sqrt{\frac{12.4EI}{mL^3}}$$ |
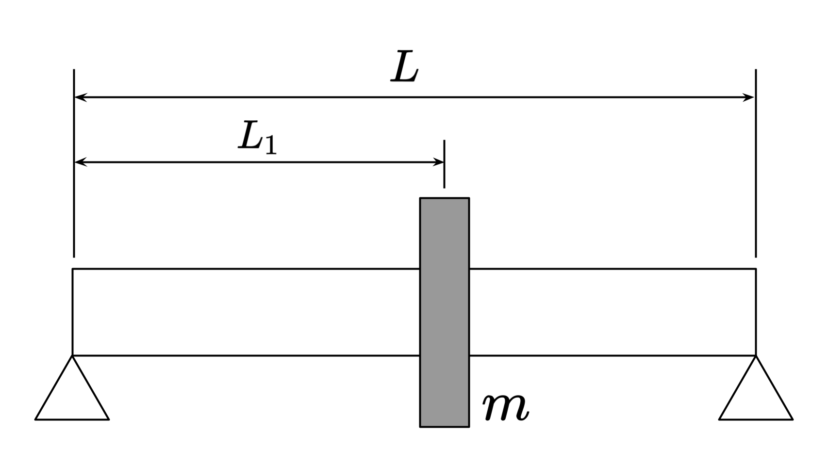
| 直径 | $$D$$ | ||
| ヤング率 | $$E$$ | ||
| 負荷質量 | $$m$$ | ||
| 長さ | $$L$$ | ||
| 長さ | $$L_1$$ |
| 断面二次モーメント | $$I=\frac{\pi D^4}{64}$$ | ||
| 危険速度 | $$\omega_c=\sqrt{\frac{3EIL}{mL_1^2(L-L_1)^2}}$$ |
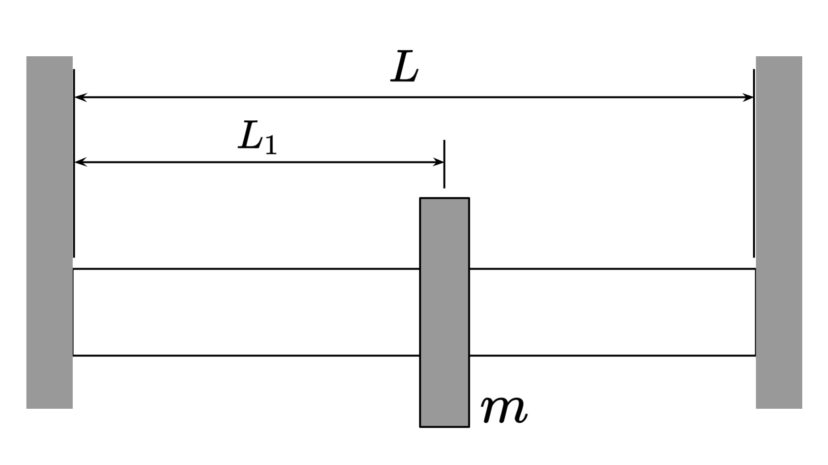
| 直径 | $$D$$ | ||
| ヤング率 | $$E$$ | ||
| 負荷質量 | $$m$$ | ||
| 長さ | $$L$$ | ||
| 長さ | $$L_1$$ |
| 断面二次モーメント | $$I=\frac{\pi D^4}{64}$$ | ||
| 危険速度 | $$\omega_c=\sqrt{\frac{3EIL^3}{mL_1^3(L-L_1)^3}}$$ |
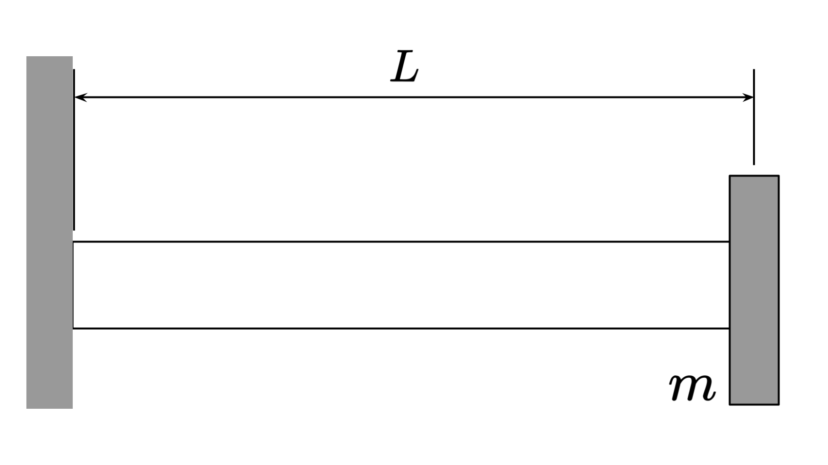
| 直径 | $$D$$ | ||
| ヤング率 | $$E$$ | ||
| 負荷質量 | $$m$$ | ||
| 長さ | $$L$$ |
| 断面二次モーメント | $$I=\frac{\pi D^4}{64}$$ | ||
| 危険速度 | $$\omega_c=\sqrt{\frac{3EI}{mL^3}}$$ |
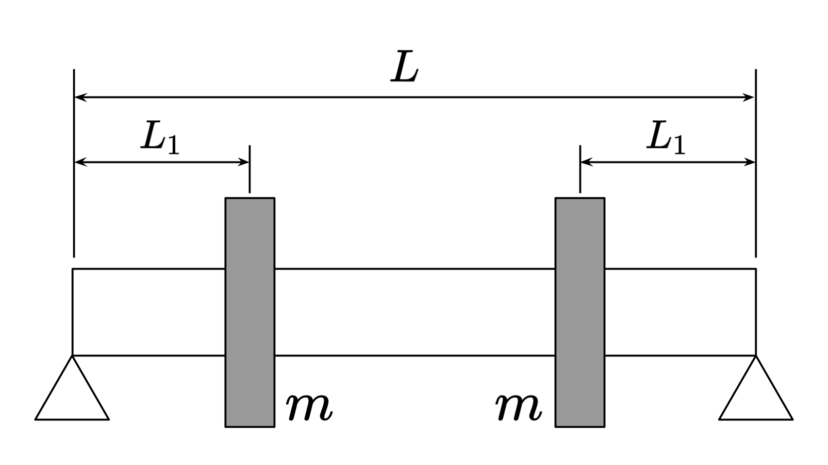
| 直径 | $$D$$ | ||
| ヤング率 | $$E$$ | ||
| 負荷質量 | $$m$$ | ||
| 長さ | $$L$$ | ||
| 長さ | $$L_1$$ |
| 断面二次モーメント | $$I=\frac{\pi D^4}{64}$$ | ||
| 危険速度 | $$\omega_c=\sqrt{\frac{6EI}{mL_1^2(3L-4L_1)}}$$ |
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

ねじり 計算ツール
エアシリンダ 計算ツール