メニュー

ボールねじ 計算ツール

計算ツール 投稿: 更新:
ホーム > 全ての記事 > 計算ツール > ボールねじ 計算ツール

注意事項

  • 免責事項をお読みの上、ご活用ください。
  • Internet Explorerでは動作しない可能性があります。Google chromeやMicrosoft Edgeなどの、他のブラウザをご利用ください
  • うまく動作しない場合は、ブラウザの履歴を削除し、画面をリロードしてみてください（要するに、キャッシュの削除です）。
  • 上記のことを試しても不具合がある場合は、お手数ですが、お問い合わせフォームよりご連絡いただければ幸いです。
搬送方式の選択

入力

動作条件入力
ストローク $$st$$
最小送り量 $$S$$
  • 加速時間
  • 等速時間※1
  • 減速時間
  • 停止時間
  • サイクルタイム
  • $$t_1$$
  • $$t_2$$
  • $$t_3$$
  • $$t_4$$
  • $$t=t_1+t_2+t_3+t_4$$
最大速度 $$v$$
  • 加速度※2
  • 減速度※2
  • $$\alpha_1=\frac{v}{t_1}$$
  • $$\alpha_3=\frac{-v}{t_3}$$
ワーク重量 $$m$$
重力加速度 $$g$$
軸方向の外部荷重 $$F_{a}$$
  1. 「ストローク」「加速時間」「減速時間」を入力すると自動計算されます。計算式は以下のとおりです。

    $$t_2=\frac{(st)}{v}-\frac{1}{2}(t_1+t_3)$$

  2. 必要事項を入力すると自動計算されます
ボールねじ特性入力
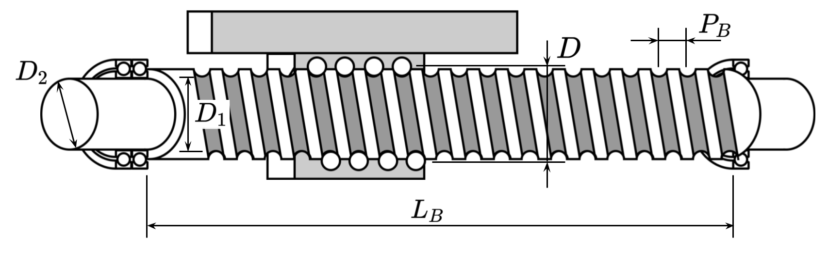
ボール中心径 $$D$$
ねじ軸谷径 $$D_1$$
ボールねじ端末軸径 $$D_2$$
ボールねじリード $$P_B$$
ボールねじ取付けピッチ $$L_B$$
ねじ軸の断面二次モーメント※1 $$I=\frac{\pi D_1^4}{64}$$
ボールねじのイナーシャ $$J_B$$
ヤング率 $$E$$
密度 $$\rho$$
案内面の摩擦係数※2 $$\mu$$
案内面の抵抗(無負荷時) $$f$$
座屈に関する端末条件係数 $$\lambda_1$$
許容回転数に関する端末条件係数 $$\lambda_2$$
ねじ軸の許容引張圧縮応力※3 $$\sigma'$$
ねじ軸の許容曲げ応力※4 $$\sigma_M'$$
ねじ軸の許容ねじり応力※5 $$\tau_T'$$
DN値 $$DN$$
基本静定格荷重 $$C_0$$
基本動定格荷重 $$C$$
静的安全係数※6 $$f_s$$
荷重係数※7 $$f_w$$
ボールねじの効率※8 $$\eta$$
予圧荷重※9,※10 $$F_p$$
  1. 必要事項を入力すると自動計算されます
  2. 一般的な環境下では、転がり摩擦係数で0.003程度、滑り摩擦係数で0.2程度です
  3. THK製では、147MPaになります（THKカタログ）
  4. THK製では、98MPaになります（THKカタログ）
  5. THK製では、49MPaになります（THKカタログ）
  6. 参考資料：THKボールねじカタログ表18
    一般産業機械、振動衝撃がない場合：
    1.0~3.5
    一般産業機械、振動衝撃がある場合：
    2.0~5.0
    工作機械、振動衝撃がない場合：
    1.0~4.0
    工作機械、振動衝撃がある場合：
    2.5~7.0
  7. 参考資料：THKボールねじカタログ表19
    振動衝撃(微)、速度v≦0.25m/s：
    1.0~1.2
    振動衝撃(小)、速度0.25<v≦1m/s：
    1.2~1.5
    振動衝撃(中)、速度1<v≦2m/s：
    1.5~2.0
    振動衝撃(大)、速度v>2m/s：
    2.0~3.5
  8. THK製では、0.9~0.95になります（THKカタログ）
  9. 最大予圧荷重の目安は、基本動定格荷重の10%程度です。正確な予圧荷重の値は、ボールねじメーカへお問い合わせください。（THKカタログより）
  10. 予圧のトルク変動率はボールねじのメーカカタログをご参照ください
モータ特性入力
モータの定格トルク $$T_{M}'$$
モータの瞬時最大トルク $$T_{Mmax}'$$
モータのブレーキトルク $$T_{MB}'$$
モータの慣性モーメント $$J_M$$
減速比 $$i$$
その他特性入力
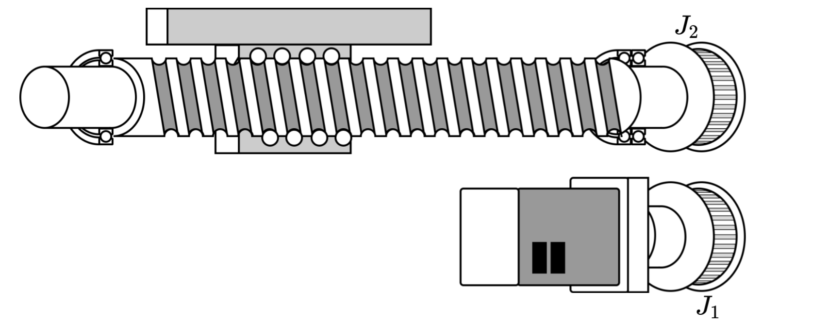
モータ軸に取付く機械要素のイナーシャ※1 $$J_1$$
負荷軸に取付く機械要素のイナーシャ※2 $$J_2$$
オイルシール等による摩擦トルク※2 $$T_f$$
ねじ軸末端にかかる曲げモーメント※3 $$M$$
  1. モータ軸の値です
  2. 負荷軸の値です
  3. 計算で求める場合は、こちらの計算ツールをご利用ください 梁のたわみ・曲げ応力 計算ツール

結果

結果(許容軸方向荷重)
  • 加速時の軸方向荷重
  • 等速時の軸方向荷重
  • 減速時の軸方向荷重
  • $$F_1=\mu mg+f+m\alpha_1+F_{a}$$
  • $$F_2=\mu mg+f+F_{a}$$
  • $$F_3=\mu mg+f+m\alpha_3-F_{a}$$
最大軸方向荷重 $$F_{max}=\max(|F_1|,|F_2|,|F_3|)$$
ねじ軸の座屈荷重 $$F_B'=\lambda_1\frac{\pi^2EI}{L^2_B}$$
ねじ軸の許容引張圧縮荷重 $$F_T'=\frac{\sigma\pi D^2_1}{4}$$
  • 安全率(座屈荷重)
  • 安全率(引張荷重)
  • $$SF_{FB}=\frac{F_B'}{F_{max}}$$
  • $$SF_{FT}=\frac{F_T'}{F_{max}}$$
転動体の許容軸方向荷重 $$F_R=\frac{C_0}{f_s}$$
結果(許容回転数)
ボールねじの回転数※1 $$N_B=\frac{60v}{P_B}$$
危険速度による許容回転数※1 $$N_1'=\frac{60\lambda_2^2}{2\pi L_B^2}\sqrt{\frac{EI\cdot10^3}{\rho\pi D_1^2/4}}$$
DN値による許容回転数※1 $$N_2'=\frac{(DN)}{D}$$
許容回転数※1 $$N'=\min(N_1', N_2')$$
安全率(回転数)※1 $$SF_N=\frac{N'}{N_B}$$
  1. ボールねじ軸の値です
結果(寿命計算)
定格寿命(総回転数) $$L=\left(\frac{C}{f_w F_{max}}\right)^3\cdot10^6$$
寿命時間 $$L_h=\frac{LP_B}{2\cdot60^2(st)/t}$$
走行距離寿命 $$L_s=LP_B$$
結果（モータ選定）
所要モータ回転数※1 $$N_M=\frac{60v}{P_B}i$$
負荷イナーシャ※1 $$J=J_1+\left(J_2+J_B+m\left(\frac{P_B}{2\pi}\right)^2\right)\cdot\frac{1}{i^2}$$
予圧によるトルク※2 $$T_p=0.05\left(\frac{P_B}{\pi D}\right)^{-0.5}\cdot\frac{F_pP_B}{2\pi}$$
外部荷重によるトルク※2 $$T_a=\frac{F_{max}P_B}{2\pi\eta}$$
所要等速トルク※1 $$T_2=\frac{T_p+T_a+T_f}{i}$$
  • 所要加速トルク※1
  • 所要減速トルク※1
  • 所要最大トルク※1
  • $$T_1=T_2+J\frac{2\pi N_M}{60t_1}$$
  • $$T_3=T_2-J\frac{2\pi N_M}{60t_3}$$
  • $$T_{max}=\max(|T_1|, |T_2|, |T_3|)$$
所要定格トルク※1 $$T_{Rated}=\sqrt{\frac{T_1^2t_1+T_2^2t_2+T_3^2t_3}{t}}$$
所要ブレーキトルク※1 $$T_{MB}=\frac{(F_a-\mu mg-f)P_B}{2\pi \eta i}$$
  • 安全率(定格トルク)
  • 安全率(瞬時最大トルク)
  • 安全率(ブレーキトルク)
  • $$SF_{T}=\frac{T_M'}{T_{Rated}}$$
  • $$SF_{Tmax}=\frac{T_{Mmax}'}{T_{max}}$$
  • $$SF_{TB}=\frac{T_{MB}'}{T_{MB}}$$
所要分解能※1 $$B=\frac{P_B}{iS}$$
イナーシャ比※1 $$J_{ratio}=\frac{J}{J_M}$$
  1. モータ軸での値です
  2. 負荷軸での値です
結果(所要ねじ軸末端径)
相当曲げモーメント $$M_e=\frac{M+\sqrt{M^2+T^2}}{2}$$
相当ねじりモーメント $$T_{e}=\sqrt{M^2+T^2}$$
所要ねじ軸末端径(対曲げ) $$D_M=\sqrt[3]{\frac{32M_e}{\pi \sigma_M}}$$
所要ねじ軸末端径(対ねじり) $$D_T=\sqrt[3]{\frac{16T_e}{\pi \tau_M}}$$
所要ねじ軸末端径 $$D_2'=\max(D_M, D_T)$$

入力

動作条件入力
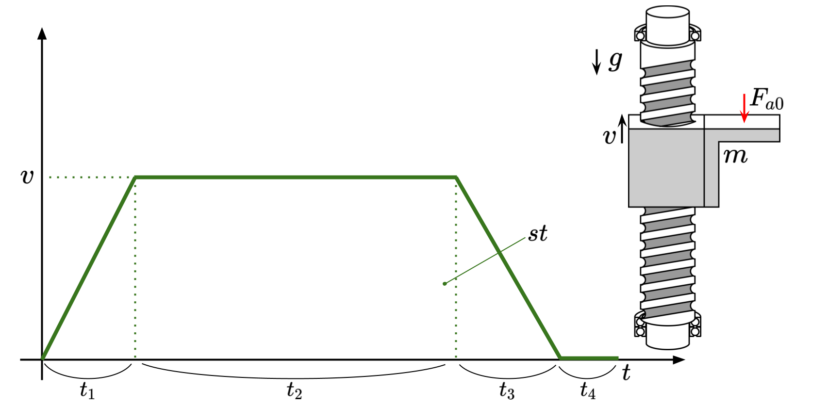
ストローク $$st$$
最小送り量 $$S$$
  • 加速時間
  • 等速時間※1
  • 減速時間
  • 停止時間
  • サイクルタイム
  • $$t_1$$
  • $$t_2$$
  • $$t_3$$
  • $$t_4$$
  • $$t=t_1+t_2+t_3+t_4$$
最大速度 $$v$$
  • 加速度※2
  • 減速度※2
  • $$\alpha_1=\frac{v}{t_1}$$
  • $$\alpha_3=\frac{-v}{t_3}$$
ワーク重量 $$m$$
重力加速度 $$g$$
軸方向の外部荷重 $$F_{a}$$
  1. 「ストローク」「加速時間」「減速時間」を入力すると自動計算されます。計算式は以下のとおりです。

    $$t_2=\frac{(st)}{v}-\frac{1}{2}(t_1+t_3)$$

  2. 必要事項を入力すると自動計算されます
ボールねじ特性入力
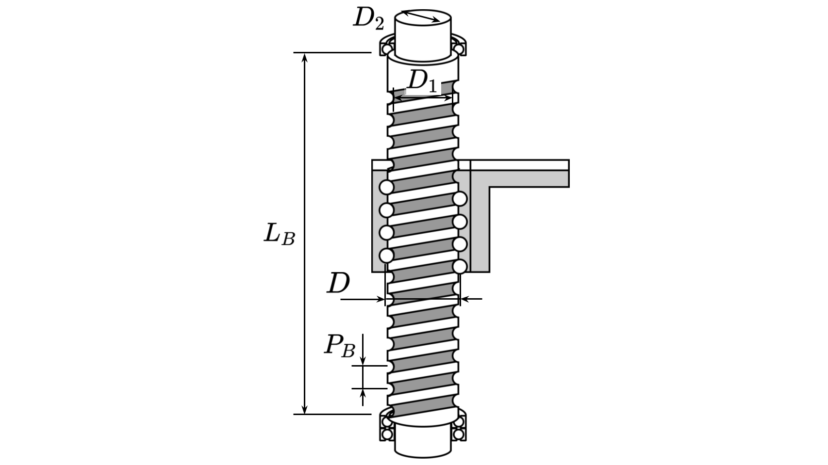
ボール中心径 $$D$$
ねじ軸谷径 $$D_1$$
ボールねじ端末軸径 $$D_2$$
ボールねじリード $$P_B$$
ボールねじ取付けピッチ $$L_B$$
ねじ軸の断面二次モーメント※1 $$I=\frac{\pi D_1^4}{64}$$
ボールねじのイナーシャ $$J_B$$
ヤング率 $$E$$
密度 $$\rho$$
案内面の抵抗(無負荷時) $$f$$
座屈に関する端末条件係数 $$\lambda_1$$
許容回転数に関する端末条件係数 $$\lambda_2$$
ねじ軸の許容引張圧縮応力※3 $$\sigma'$$
ねじ軸の許容曲げ応力※4 $$\sigma_M'$$
ねじ軸の許容ねじり応力※5 $$\tau_T'$$
DN値 $$DN$$
基本静定格荷重 $$C_0$$
基本動定格荷重 $$C$$
静的安全係数※6 $$f_s$$
荷重係数※7 $$f_w$$
ボールねじの効率※8 $$\eta$$
予圧荷重※9,※10 $$F_p$$
  1. 必要事項を入力すると自動計算されます
  2. 一般的な環境下では、転がり摩擦係数で0.003程度、滑り摩擦係数で0.2程度です
  3. THK製では、147MPaになります（THKカタログ）
  4. THK製では、98MPaになります（THKカタログ）
  5. THK製では、49MPaになります（THKカタログ）
  6. 参考資料：THKボールねじカタログ表18
    一般産業機械、振動衝撃がない場合：
    1.0~3.5
    一般産業機械、振動衝撃がある場合：
    2.0~5.0
    工作機械、振動衝撃がない場合：
    1.0~4.0
    工作機械、振動衝撃がある場合：
    2.5~7.0
  7. 参考資料：THKボールねじカタログ表19
    振動衝撃(微)、速度v≦0.25m/s：
    1.0~1.2
    振動衝撃(小)、速度0.25<v≦1m/s：
    1.2~1.5
    振動衝撃(中)、速度1<v≦2m/s：
    1.5~2.0
    振動衝撃(大)、速度v>2m/s：
    2.0~3.5
  8. THK製では、0.9~0.95になります（THKカタログ）
  9. 最大予圧荷重の目安は、基本動定格荷重の10%程度です。正確な予圧荷重の値は、ボールねじメーカへお問い合わせください。（THKカタログより）
  10. 予圧のトルク変動率はボールねじのメーカカタログをご参照ください
モータ特性入力
モータの定格トルク $$T_{M}'$$
モータの瞬時最大トルク $$T_{Mmax}'$$
モータのブレーキトルク $$T_{MB}'$$
モータの慣性モーメント $$J_M$$
減速比 $$i$$
その他特性入力
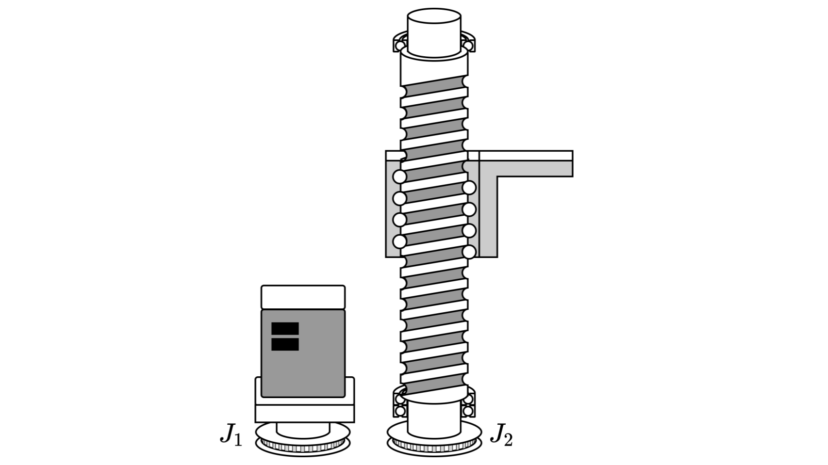
モータ軸に取付く機械要素のイナーシャ※1 $$J_1$$
負荷軸に取付く機械要素のイナーシャ※2 $$J_2$$
オイルシール等による摩擦トルク※2 $$T_f$$
ねじ軸末端にかかる曲げモーメント※3 $$M$$
  1. モータ軸の値です
  2. 負荷軸の値です
  3. 計算で求める場合は、こちらの計算ツールをご利用ください 梁のたわみ・曲げ応力 計算ツール

結果

結果(許容軸方向荷重)
  • 加速時の軸方向荷重
  • 等速時の軸方向荷重
  • 減速時の軸方向荷重
  • $$F_1=mg+f+m\alpha_1+F_{a}$$
  • $$F_2=mg+f+F_{a}$$
  • $$F_3=mg+f+m\alpha_3-F_{a}$$
最大軸方向荷重 $$F_{max}=\max(|F_1|,|F_2|,|F_3|)$$
ねじ軸の座屈荷重 $$F_B'=\lambda_1\frac{\pi^2EI}{L^2_B}$$
ねじ軸の許容引張圧縮荷重 $$F_T'=\frac{\sigma'\pi D^2_1}{4}$$
  • 安全率(座屈荷重)
  • 安全率(引張荷重)
  • $$SF_{FB}=\frac{F_B'}{F_{max}}$$
  • $$SF_{FT}=\frac{F_T'}{F_{max}}$$
転動体の許容軸方向荷重 $$F_R=\frac{C_0}{f_s}$$
結果(許容回転数)
ボールねじの回転数※1 $$N_B=\frac{60v}{P_B}$$
危険速度による許容回転数※1 $$N_1'=\frac{60\lambda_2^2}{2\pi L_B^2}\sqrt{\frac{EI\cdot10^3}{\rho\pi D_1^2/4}}$$
DN値による許容回転数※1 $$N_2'=\frac{(DN)}{D}$$
許容回転数※1 $$N'=\min(N_1', N_2')$$
安全率(回転数)※1 $$SF_N=\frac{N'}{N_B}$$
  1. ボールねじ軸の値です
結果(寿命計算)
定格寿命(総回転数) $$L=\left(\frac{C}{f_w F_{max}}\right)^3\cdot10^6$$
寿命時間 $$L_h=\frac{LP_B}{2\cdot60^2(st)/t}$$
走行距離寿命 $$L_s=LP_B$$
結果（モータ選定）
所要モータ回転数※1 $$N_M=\frac{60v}{P_B}i$$
負荷イナーシャ※1 $$J=J_1+\left(J_2+J_B+m\left(\frac{P_B}{2\pi}\right)^2\right)\cdot\frac{1}{i^2}$$
予圧によるトルク※2 $$T_p=0.05\left(\frac{P_B}{\pi D}\right)^{-0.5}\cdot\frac{F_pP_B}{2\pi}$$
外部荷重によるトルク※2 $$T_a=\frac{F_{max}P_B}{2\pi\eta}$$
所要等速トルク※1 $$T_2=\frac{T_p+T_a+T_f}{i}$$
  • 所要加速トルク※1
  • 所要減速トルク※1
  • 所要最大トルク※1
  • $$T_1=T_2+J\frac{2\pi N_M}{60t_1}$$
  • $$T_3=T_2-J\frac{2\pi N_M}{60t_3}$$
  • $$T_{max}=\max(|T_1|, |T_2|, |T_3|)$$
所要定格トルク※1 $$T_{Rated}=\sqrt{\frac{T_1^2t_1+T_2^2t_2+T_3^2t_3}{t}}$$
所要ブレーキトルク※1 $$T_{MB}=\frac{(F_a+mg-f)P_B}{2\pi \eta i}$$
  • 安全率(定格トルク)
  • 安全率(瞬時最大トルク)
  • 安全率(ブレーキトルク)
  • $$SF_{T}=\frac{T_M'}{T_{Rated}}$$
  • $$SF_{Tmax}=\frac{T_{Mmax}'}{T_{max}}$$
  • $$SF_{TB}=\frac{T_{MB}'}{T_{MB}}$$
所要分解能※1 $$B=\frac{P_B}{iS}$$
イナーシャ比※1 $$J_{ratio}=\frac{J}{J_M}$$
  1. モータ軸での値です
  2. 負荷軸での値です
結果(所要ねじ軸末端径)
相当曲げモーメント $$M_e=\frac{M+\sqrt{M^2+T^2}}{2}$$
相当ねじりモーメント $$T_{e}=\sqrt{M^2+T^2}$$
所要ねじ軸末端径(対曲げ) $$D_M=\sqrt[3]{\frac{32M_e}{\pi \sigma_M'}}$$
所要ねじ軸末端径(対ねじり) $$D_T=\sqrt[3]{\frac{16T_e}{\pi \tau_M'}}$$
所要ねじ軸末端径 $$D_2'=\max(D_M, D_T)$$

免責事項

  • 計算ツールおよびその計算結果について、当ブログがその内容を保証するものではありません。
  • 計算ツールおよびその計算結果のご利用により、利用者または第三者に生じた損害や不利益、トラブルについて、当ブログはその一切の責任を負いません。
  • 計算ツールの内容について、予告なしに変更・削除を行う場合があります。これによって生じるいかなる損害や不利益についても、当ブログが責任を負うものではありません。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

ものづくりのススメ
りびぃ

この記事を書いた人

機械設計エンジニア: りびぃ

りびぃが書いた記事一覧を見る

コンベヤ搬送 計算ツール

ねじり 計算ツール

console.log("postID: 9641");console.log("カウント: 22458");