【解説】2つの平板間の熱応力の計算方法

機械工学を学んだ人にとって熱応力の問題といえば、材料力学で学んだなと懐かしく感じる方は多いと思います。

習ったきり、そういえばあまり使っていないな・・・という人も多いと思いますが、実は実際の機械設計で必要になるケースがあります。

特に

• 鉄とアルミとを組みわせたモジュールの設計をしている
• 金属と樹脂とを組み合わせたモジュールを設計している

という場合において、近くに熱源があるような場合においては、この熱応力によるトラブルに気をつける必要があります。

熱源といえば「ヒータ」などがありますが、

という方も侮れません。

例えば

• 容量の大きいコントローラが近くにある場合
• 高出力のカメラ用照明を使っている場合
• 高回転部が近くにある場合
• 直射日光が当たったり、エアコンがない現場環境の場合

というような状況にある場合、それらが熱源となり熱応力によるトラブル発生の原因になったりします。

なのでもしこのようなトラブルが予想される場合には、事前に設計で対策しておきたいところですよね。

ということで今回は、このような検討に役立つ「接合された2つの平板に発生する熱応力」についてわかり易く解説をしていきます。

2つの平板間の熱応力

熱応力とはどんな時に発生するのか

材料は、温度が上がると膨張し、温度が下がると収縮します。この材料の変形が、材料の拘束などによって妨げられると、それに相応する応力が材料に発生します。

この応力のことを熱応力と呼びます。

特に実際のものづくりにおいても、熱応力が問題となるのは、以下のようなケースです。

• 接合された2つの材料の間の、温度差が大きいとき
• 接合された2つの材料の間の、線膨張係数の差が大きいとき

2つの平板間に働く熱応力の計算

2つの平板間に働く熱応力の計算では、いきなり応力について考えるのではなく、まずはひずみから考えていきます。

そしてこのひずみは、「熱ひずみ」と「拘束によるひずみ」とに分けて考えるのがポイントです。

ここで例題を紹介します。

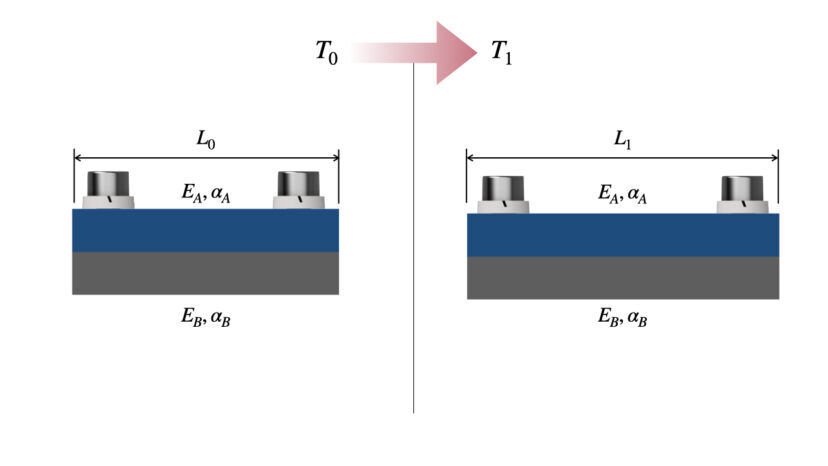
下の図のように、板の断面積S_A、ヤング率E_A、線膨張係数α_Aである材料Aと、板の断面積S_Bヤング率E_B、線膨張係数α_Bである材料Bとを、温度T₀の環境においてボルトで接合します。このとき、2つの材料の長さはL₀とし、2つの材料の間に応力は発生していないものとします。

この状態から温度T₁まで加熱をしたときの、熱応力について求めていきます。

2つの平板が接合されていなかった場合について考える

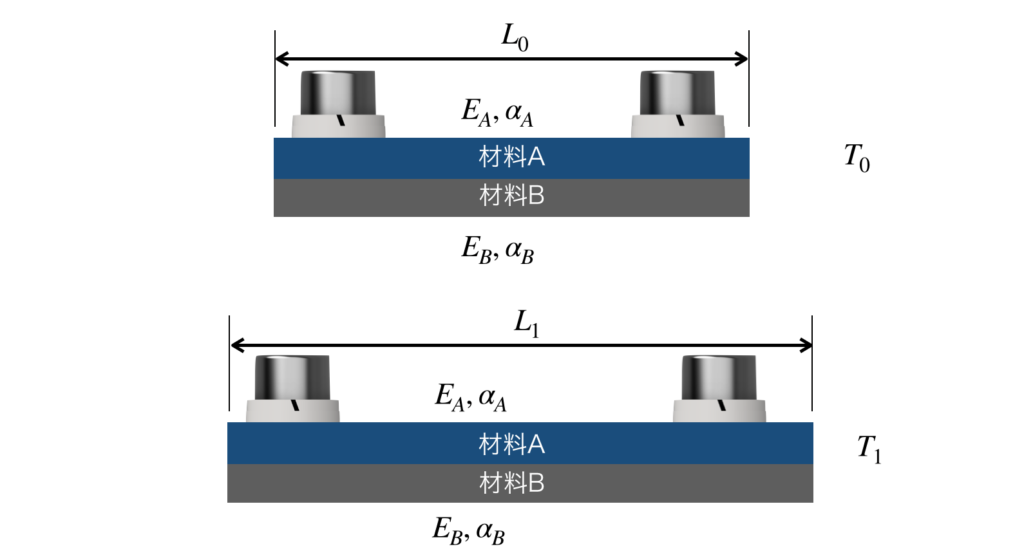
まずは、2つの平板が接合されていなかったら、どうなっていたかについて考えます。

温度T₁の時の、材料1の長さをL_1A、材料2の長さをL_1Bとします。仮に線膨張係数の値が、材料Aの方が大きいとすると、ぞれぞれの材料は膨張によって、以下の図のようになります（逆でも構いません）。

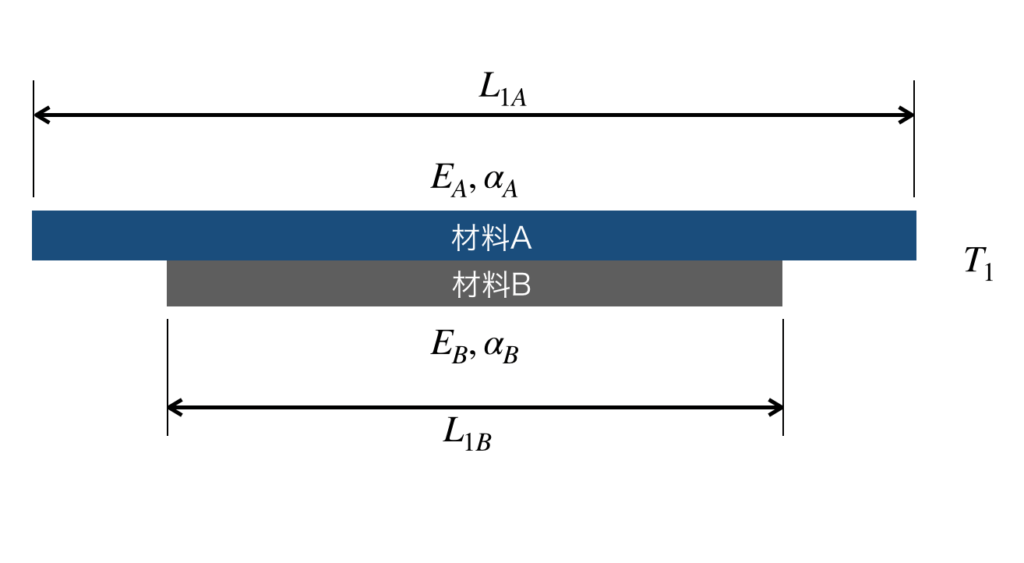
このように、材料の温度変化によって発生するひずみのことを、熱ひずみと呼び、以下のような式で表されます。

$$\begin{align}
\varepsilon_T=\alpha\Delta T
\end{align}$$

よって、材料A・材料Bそれぞれに発生する熱ひずみの大きさは、以下のように表されます(※$\varepsilon_{TA}$と$\varepsilon_{TB}$は方向が逆なので、(2)式にマイナスをかけています)。

$$\begin{cases}
\varepsilon_{TA}=\alpha_A(T_1-T_0)\cdots(1)\\
\varepsilon_{TB}=-\alpha_B(T_1-T_0)\cdots(2)
\end{cases}$$

材料が受ける拘束を考える

続いては、ボルト接合によって材料が受ける拘束について考えていきます。

しかし実際には、2つの平板はボルトで接合されているので、変形が妨げられます。

材料Aにとっては、本来ならばL_1Aまで膨張できたのですが、材料Bに引きずられていることで、長さL₁まで縮められています。

逆に材料Bにとっては、本来ならばL_1Bまでしか膨張しないのですが、材料Aに引きずられていることで、長さL₁まで伸ばされてしまっています。

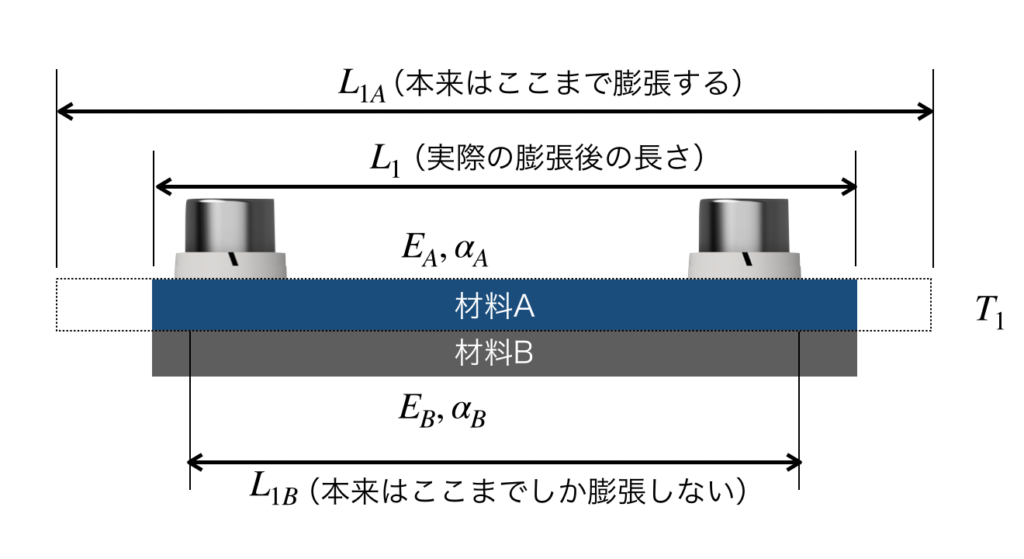
実はこの現象は、以下のように言い換えることができます（ここでいう〇〇荷重を、見かけの力と言うこととします）。

• 材料1はL_1Aまで変形しようとしたが、L₁までしか変形できないように圧縮荷重を受けて、ひずんだ
• 材料2はL_1Bまでしか変形しないはずだったが、L₁まで変形するよう引張荷重を受けて、ひずんだ

これを式で表すと、以下のとおりとなります($\varepsilon_{PA}$と$\varepsilon_{PB}$は方向が逆ですが、この方向の違いは$\sigma_A$と$\sigma_B$に実際に代入される値に内包することとしているため、ここでは符号をマイナスにするなどの処理はしません)。

$$\begin{align}
\varepsilon_{PA}=\frac{\sigma_A}{E_A}\cdots(3)\\
\varepsilon_{PB}=\frac{\sigma_B}{E_B}\cdots(4)
\end{align}$$

「変形量の総和が等しい」という条件を使う

材料A・材料Bそれぞれについて、「熱ひずみ」および「見かけの力によるひずみ」が発生するのですが、最終的な変形量はL₁となり等しくなるという条件を使います。

「ひずみ」に「変形前の寸法」を掛け算すると、変形量が求められることを利用すると、変形量は以下のように表すことができます。

$$(\varepsilon_{TA}+\varepsilon_{PA})\cdot L_{0}+(\varepsilon_{TB}+\varepsilon_{PB})\cdot L_{0}=0$$
$$\alpha_A(T_1-T_0)+\frac{\sigma_A}{E_A}-\alpha_B(T_1-T_0)+\frac{\sigma_B}{E_B}=0\cdots(5)$$

ただし、(5)式は、未知数が2つ(σ_A、σ_B）に対して、式が1つしかないため、式を解くためにはもう一つ関係式が必要となります。

釣り合いの式を立てる

もう一つの関係式が必要であるため、ここで材料が受ける力の釣り合いから式を立てていきます。

接合された2種類の材料が膨張するときに、それぞれの材料が受ける見かけの力をP_A、P_Bとします。

すると、力の釣り合いより以下の関係式が成り立ちます。

$$P_A+P_B=0\cdots(6)$$

また応力の定義より、(5)式は以下のように書き換えることができます。

$$\alpha_A(T_1-T_0)+\frac{P_A}{S_AE_A}-\alpha_B(T_1-T_0)+\frac{P_B}{S_BE_B}=0\cdots(7)$$

(6)式、(7)式を解くことによって、P_A、P_Bは以下のようになります。

$$P_A=\frac{S_AS_BE_AE_B}{S_BE_B-S_AE_A}(\alpha_B-\alpha_A)(T_1-T_0)\cdots(8)$$

$$P_B=\frac{S_AS_BE_AE_B}{S_AE_A-S_BE_B}(\alpha_B-\alpha_A)(T_1-T_0)\cdots(9)$$

よって、各材料に発生する応力は、各材料の断面積で割って以下のように求められます。

$$\begin{align}
\sigma_A=\frac{S_BE_AE_B}{S_BE_B-S_AE_A}(\alpha_B-\alpha_A)(T_1-T_0)\\
\sigma_B=\frac{S_AE_AE_B}{S_AE_A-S_BE_B}(\alpha_B-\alpha_A)(T_1-T_0)
\end{align}$$

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...