こんにちはー、りびぃです。
普段はFA(ファクトリー・オートメーション)の業界で機械設計をやっている現役のエンジニアです。
私は今まで多数の業界の生産工程の自動化の設計に携わってきましたが、そんな中でもしばしばよく使うのが「材料力学」の知識です。
機械工学系の学科出身の方は、必修として習った人も多いのではないでしょうか?
そしてその中でも、材料のたわみ、曲げ強度の計算は比較的行う印象です。
そうそう、集中荷重とか分布荷重とかってやったなー!
最近では手計算だけではなく、CADモデルを使って解析をすることによって強度やたわみを評価することも多くなってきました。
しかし、計算をしている中で、
む・・・?これってあってるのか・・・?
というような、何か違和感を感じるような計算結果になってしまったという経験をしたことがある方は、結構多いのではないでしょうか?
それはもしかすると、梁の計算において「荷重」に関する認識に誤りがあるからかもしれません。
いくら正確な計算をしたところで、そもそも計算の前提が間違っていたら何回やっても正解にたどりつけないですからね・・・
そこで今回は、梁の計算において重要な荷重に関する知識について、わかり易く解説をしていきます。
まず、梁にかかる荷重については大きく分けると3種類あることを抑えておきましょう。
その3種類とは
になります。
では一つずつ解説をしていきます。
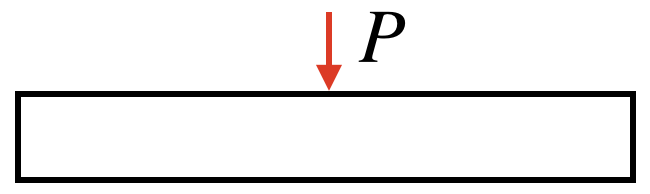
集中荷重とは、
1点に集中して作用する荷重のことを言います。
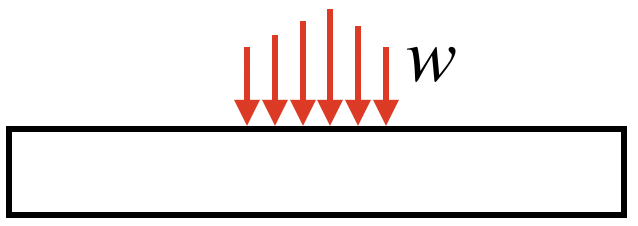
ある領域に分布して作用する力のことを言います。単位は[N/mm]です。
つまり、「1mmあたりに換算したときに作用している荷重」のことを言います。
荷重の分布は、下の図のように、領域によって梁に作用する荷重の大きさがばらばらであることもあります。
分布荷重の中でも、分布が一様(どの領域を切りとっても、分布荷重が同じになる)であるものを「等分布荷重」と言います。

梁が一様な形状(途中で太くなったり、細くなったりしない)であり、
かつ水平に固定されているとき、
材料の自重による外力は「等分布荷重」として計算できます。
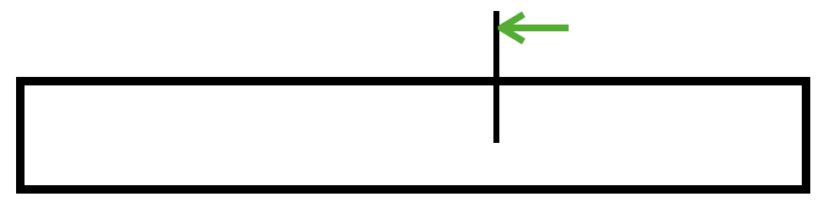
回転力を作用させるような力のことを言います。単位は[N・m]です。

モデル図で書くとどんな状況なのかがわかりづらいですが、例えば梁に棒を立てて、曲げ荷重をかけるような場合が該当します。
厳密にいうと、現実の世界に「集中荷重」は存在しません。
「いきなり意味のわからないことを言い出してる」と思う方もいると思いますので、詳しくお話しします。
集中荷重は「ある一点」に荷重がかかっているとみなすと定義されておりますが、
そもそも「点」は「領域」の概念を持ちません。
つまり、「集中荷重」=「幅がゼロの分布荷重」ということになります。
高校の数ⅢCを勉強した人はわかると思いますが、もう少し詳しく説明します。
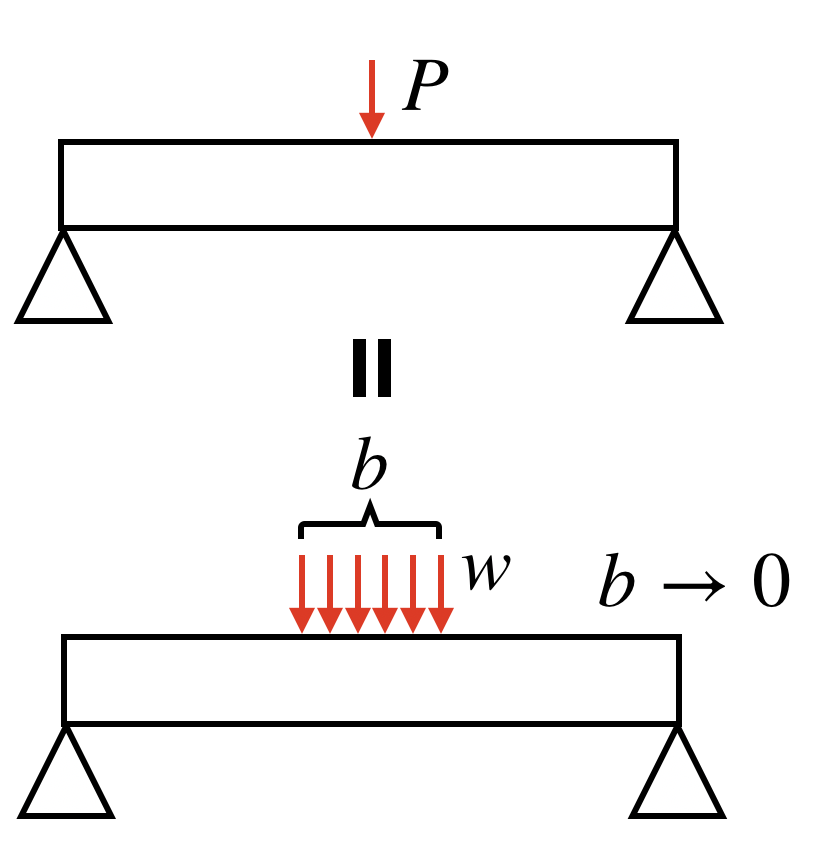
例えば、P=100 N(だいたい10kgの米袋を持つのに必要な力)の「集中荷重」が梁にかかっているとします。
これは、分布荷重w N/mmを幅b mmにかけたとき、P=wbの関係を保ったまま、bを0に近づけていくことを意味します。
$$\begin{align}
P=wb\\
b\rightarrow 0
\end{align}$$
b=1 mmのときにw=P=100Nとなります。しかし、b=1 mmは十分小さな幅であるかもしれませんが「一点にかかっている荷重」ではありません。
bをもっと小さくしてb = 0.001 mmとすると、「P=wb」となるためにはw=100,000 N/mmである必要があります。
しかしb=0.001 mmもまた「一点にかかっている荷重」ではありません。
この調子で、bをどんどん0 mmに近づけていくと、
$$\begin{align}
w\rightarrow\infty\\
\end{align}$$
となります。
こんなとてもない荷重が材料にかかっていれば、どんなに強度の高い部材であっても理論上は100%壊れます。
しかし、実際の建物に使われている梁で、たった100Nの荷重で壊れる梁を私は聞いたことがありません。
なぜなら現実の世界では、材料に荷重を加える際には「領域」が存在するからです。
例えば、シャーペンの先端を梁に押し付けたとしても、直径0.5mm程度の領域があります。
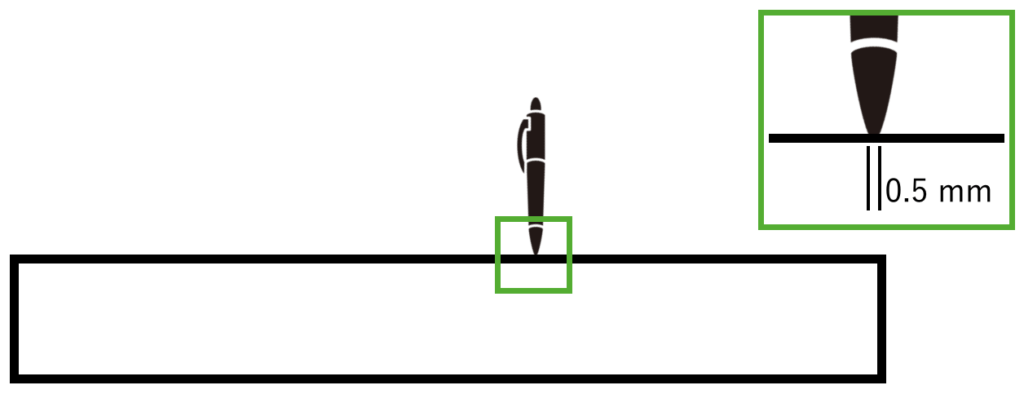
では、「集中荷重」はなんの意味があるのか?
それは、計算が簡単になるということです。
基本的に分布荷重の方が計算が複雑であり、荷重の分布が複雑であるほど、計算が複雑になります。
普通は積分をする必要があります。
そもそも、どのような分布になっているかがわからなければ、計算をすることすらできません。
ところが、「集中荷重」としてみなせる場合は、これらのことを考慮しなくても計算できてしますのです。
実際には、どのような場合が「集中荷重」とみなせるか?
というのは、時と場合によります。
例えば、全長4mの梁に対して、分布の幅が1mmであれば、集中荷重としてみなせるかもしれませんが、
全長3mmの梁に対して、分布の幅が1mmであれば、集中荷重とみなせない可能性があります。
また、求められている計算の精度にもよりますので、
実際の設計で、「集中荷重」と「分布荷重」のどちらを使って計算をするかは、
各設計者の「感覚」でやっていることが多いです。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

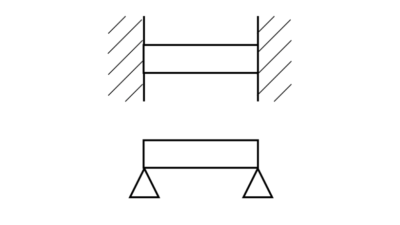
梁の支持方法と、使い分けの方法
断面二次モーメントってどんな意味か? についての解説
