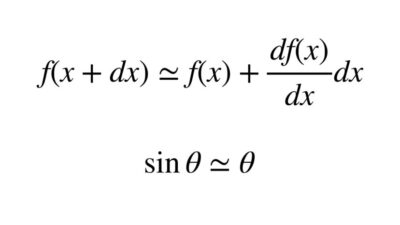
ものづくりにおいて、バネはしばしば使われる機械要素です。
多くの場合は、すでに部品の中に組み込まれていることが多いです。
しかし、バネ単体を購入して装置に組み込むこともあり、
例えば自転車のブレーキのような、ワイヤーを引っ張ったあとの戻し用として組み込んだりすることがあります。
私は治具などの設計で使用することがあります。
そんなバネについてですが、一見単純なように見えて、実は奥が深い部品でもあります。
今回はそんなバネについて、力学的な観点からお話をしていきます。
まずはフックの法則についてお話ししてきます。
ばねの伸び縮みについての現象は、中学の理科で習いますが、一度さらっとお話ししていきます。
フックの法則とは、バネの反力は、バネの伸びに比例するという関係があることを示したもので、以下のように表されます。
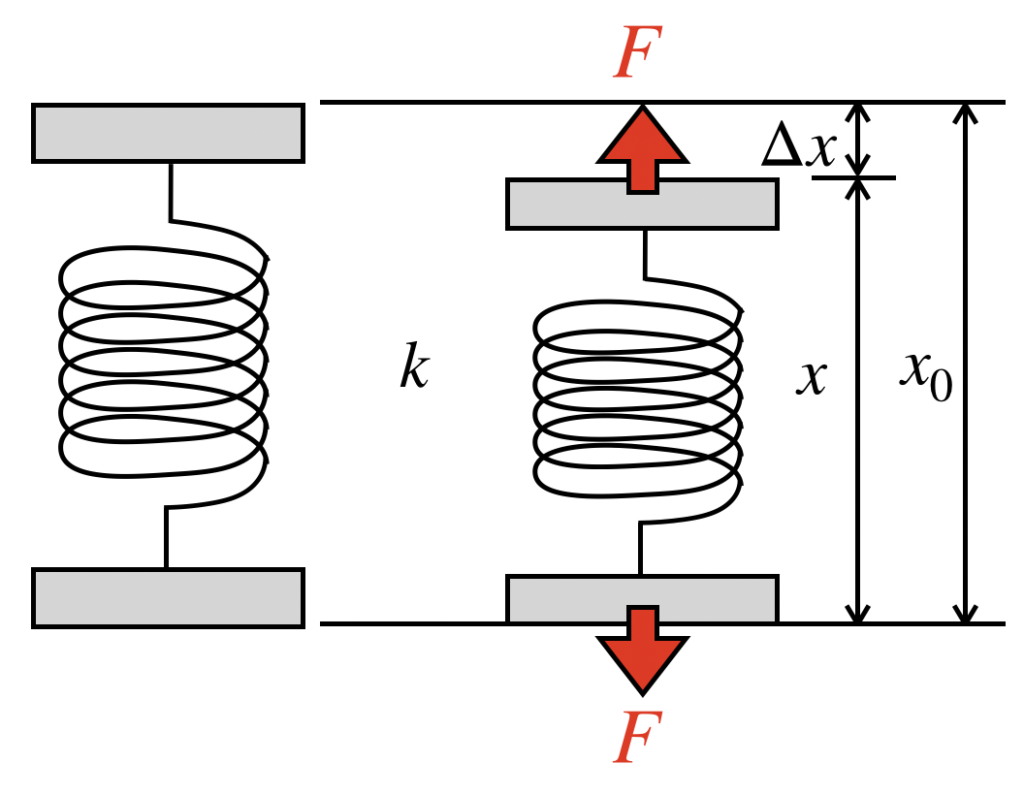
$$F=-k\Delta x=-k(x-x_0)\cdots(1)$$
F:バネによる反力
k:バネ定数
Δx:バネの伸び
x:伸び縮みした後のバネの位置
x0:自然長
フックの法則の右辺にマイナスがついておりますが、このマイナスは「バネに加えられた荷重とは反対方向に反力が発生する」という意味になります。
例えば、自然長の状態からバネをxだけ縮めると、バネが元の形状に戻る方向に、大きさk(x-x0)の力が発生します。
簡単のために、2つのバネを直列に繋いだ場合について、2つのバネ定数が同じであるときの現象について考えてみましょう。
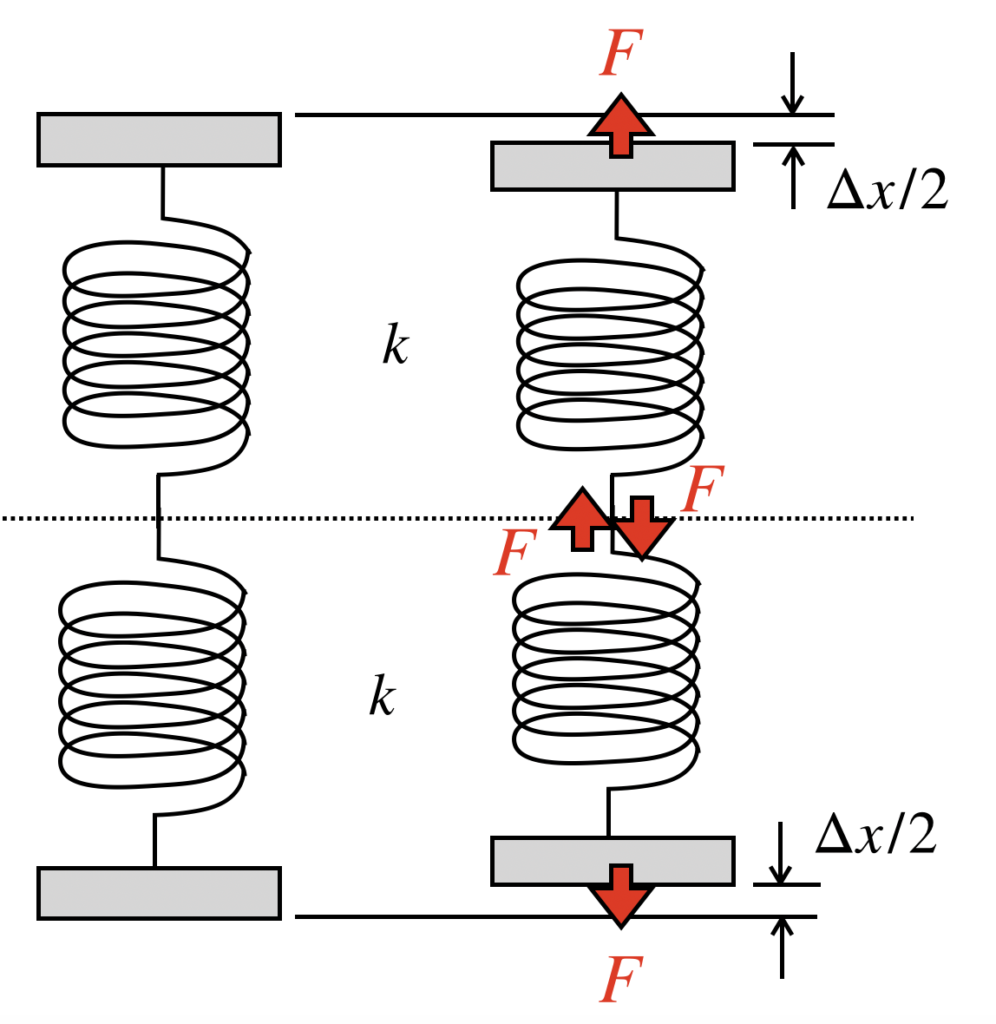
2つのバネを直列に繋いだ状態で、自然長からΔxだけ縮めることを考えます。
これは、バネ1つあたり、自然長からΔx/2だけ縮めた時と同じであると言えます。
そのため、バネ1つあたりに発生する力は、以下の式で表すことができます。
$$F=-k\frac{\Delta x}{2}=-k(\frac{x-x_0}{2})\cdots(2)$$
もう一つのバネについても同様の力が発生するのですが、注意していただきたいのは「バネを直列に繋いだ場合、発生するバネの反力は、お互いのバネ同士で打ち消しあう」ということです。
下の図で、2つのバネそれぞれに着目してみると、バネ1がバネ2に与える反力と、バネ2がバネ1に与える反力は向きが逆です。
さらに今回の場合では、2つのバネのバネ定数は同じであるため、反力の大きさも同じとなります。
このことから、発生する反力を、お互いのバネ同士で打ち消し合っていることがわかります。
そのため、バネ全体に発生している反力も、
$$F=-k\frac{\Delta x}{2}=-k(\frac{x-x_0}{2})\cdots(2)$$
となります。
そのため、「バネの伸び(縮み)の量が同じである時、バネを1つだけ使用したときに比べて、2つのバネを直列に繋ぐと、反力が小さくなる」ということがわかります。
ちなみに、この直列に繋がれたバネを1つのバネとしてみなす(合成する)場合、以下の式のとおりとなります。
$$\begin{align}
\frac{1}{K}&=\frac{1}{k_1}+\frac{1}{k_2}\\
&=\frac{1}{k}+\frac{1}{k}\\
&=\frac{1}{k/2}
\end{align}$$
K:合成後のバネ定数
k1:バネ1のバネ定数
k2:バネ2のバネ定数
このことから「バネを直列に繋ぐと、バネ定数が減少したとみなすことができる」ともいうことができます。
これを利用して、バネ定数を下げたいときに、
という2つの方法から選択をすることができます。
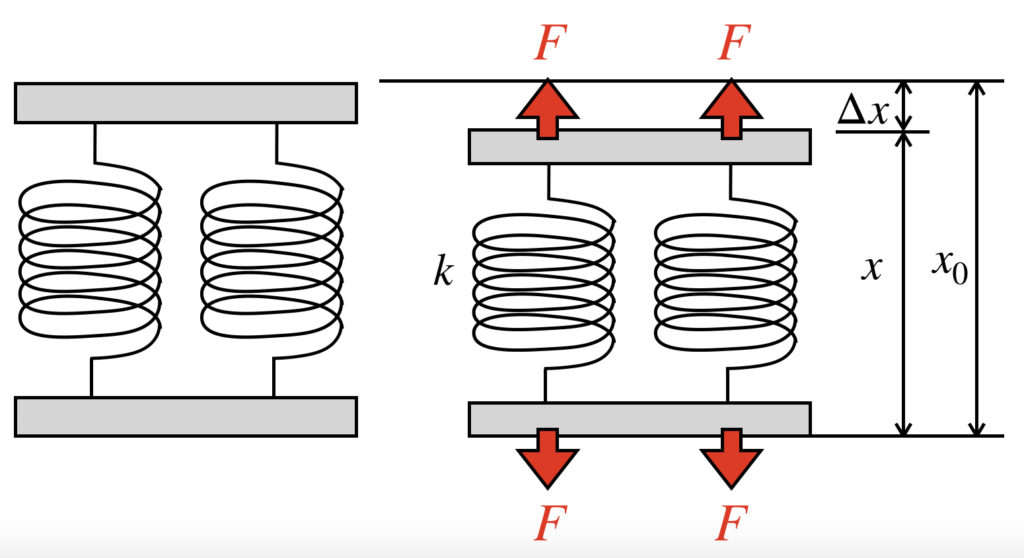
ここでも簡単のために、2つのバネを並列に繋いだ場合について、2つのバネ定数が同じであるときの現象について考えてみましょう。
2つのバネを並列に繋いだ状態で、自然長からΔxだけ縮めることを考えます。
並列の場合、バネの伸び(縮み)の量が同じであれば、バネ1つあたりに発生するバネの反力は、バネ1本の時と同じになります。
しかし、並列の場合、同じ方向に反力が発生しているバネがもう1つありますので、バネ全体としては反力は足し算になります。
$$\begin{align}
F&=-(k_1(x-x_0)+k_2(x-x_0)\\
&=-(k(x-x_0)+k(x-x_0))\\
&=-2k(x-x_0)(=-2k\Delta x)\cdots(3)
\end{align}$$
そのため、「バネの伸び(縮み)の量が同じである時、バネを1つだけ使用したときに比べて、2つのバネを並列に繋ぐと、反力が大きくなる」ということが言えます。
ちなみに、この並列に繋がれたバネを1つのバネとしてみなす(合成する)場合は、以下の式のとおりとなります。
$$\begin{align}
K&=k_1+k_2\\
&=k+k\\
&=2k
\end{align}$$
K:合成後のバネ定数
k1:バネ1のバネ定数
k2:バネ2のバネ定数
このことから「バネを並列に繋ぐと、バネ定数が増加したとみなすことができる」ともいうことができます。
これを利用して、バネ定数を上げたいときに、
という2つの方法から選択をすることができます。
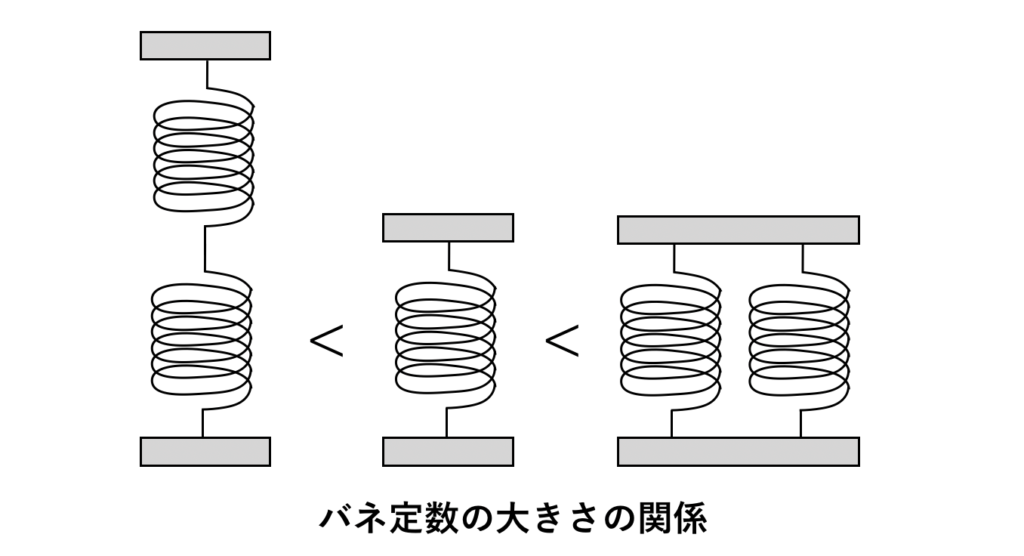
以上のことをまとめると、バネ全体の伸び・縮み量、およびバネ定数が同じであるとき、バネ定数の大きさは、
「直列」<「ばね単体」<「並列」という関係になります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

自分で自分を持ち上げるのが不可能なことの証明【力学的に説明します】
力学で出てくるテイラー展開と近似【式の導出でよく使います】