今回は主に高校生向けにこのような問題の解き方について、お答えしていきます。
問題
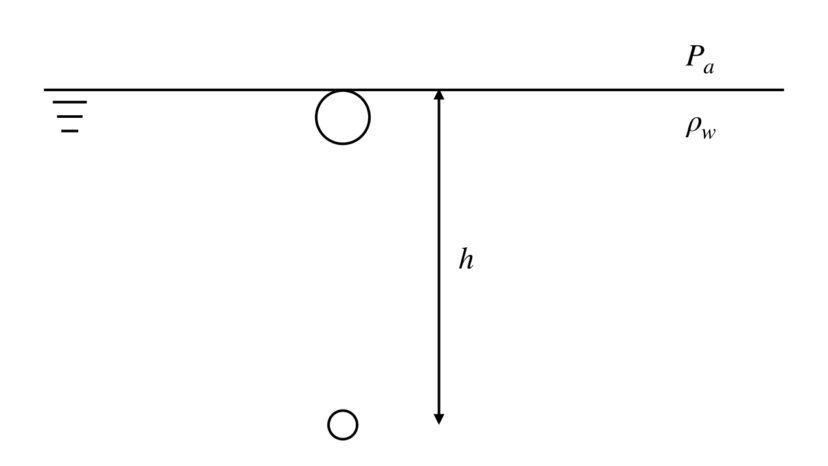
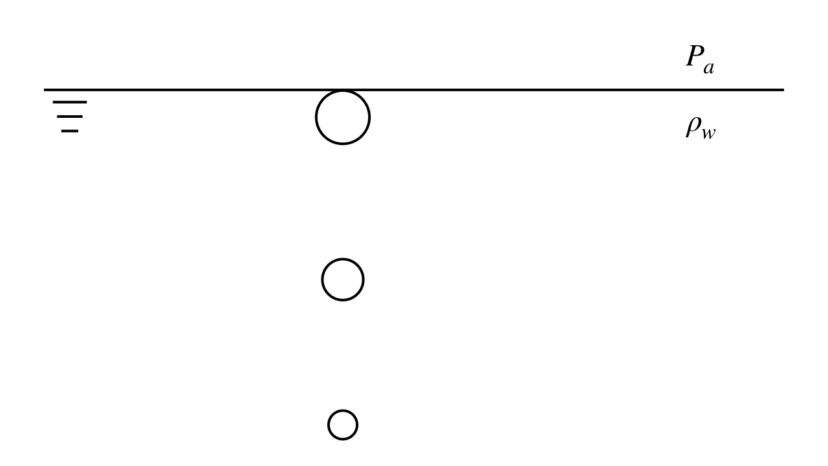
水深hの場所で発生した直径d0の気泡が、水面まで浮上していったとすると、水面における気泡の直径はいくつでしょうか。
ここで、気泡は球形とみなせるとし、水の密度をρw、空気圧をPa、重力をgとします。
また、気泡内の空気は理想気体であるとし、気泡および液体の温度はどの場所でも一定であるとします。
ただし、気泡の直径は水深に比べて十分小さいとします。
水中にある物体は、水深の深いところにあるほど水から力を受けます。

よく水族館の深海魚のコーナーに行くと、
「カップ麺の容器を水深数千メートルまで持っていくと、水で押しつぶされて容器が小さくなる」
みたいな展示をよく見かけますし、
「プールの深いところに潜ると、水で耳が痛くなったり」
しますよね。
水中の気泡もまた水圧の影響を受けますが、ここでポイントなのが、気体は圧力や力を加えると縮小するので、水から受ける力によって気泡の大きさが変わる(逆に気体に加わる力が減少すると、気体は膨張する)ということです。
そんな水圧に関する問題は、高校物理でたまに出てきますが、出てくる頻度がそこまで多くないので、不意に出題されるとやり方を忘れていることが多いです。
そこで今回は、水圧に関する問題の解説をしていきたいと思います。
最近はコロナウイルスの影響で、あまり自宅から出れない状況が続いていますが、今回のような記事を高校物理の勉強に役立っていただければ幸いです。
いったん気泡のことはちょっと横に置いておいて、一般に水深hの場所にある、面積がAである面にかかる力を考えていきましょう。
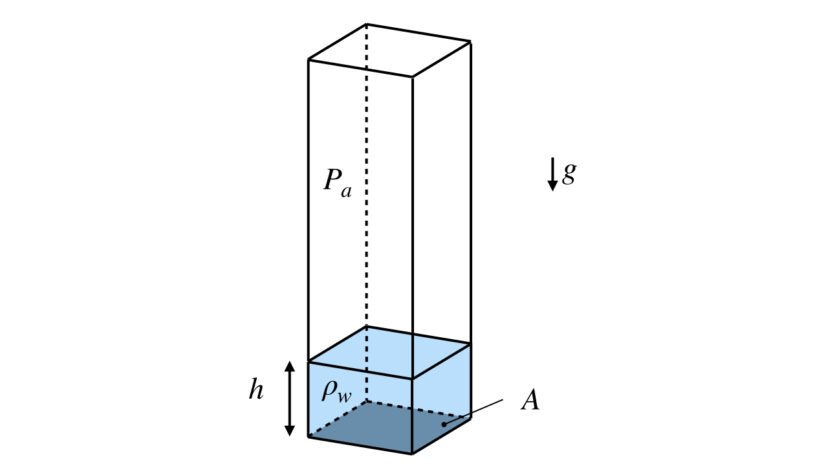
まず、水深hの場所にある面が受けるのは
「空気圧による力:Fa」と「水による力:Fw」を足したものなります。
「空気圧による力」は、空気圧Paが与えられていることから、以下の式で求める事ができます。
$$F_a=P_aA$$
続いて「水による力」は、密度ρwが与えられていることから、以下の式で求める事ができます。
$$F_w=\rho Ahg$$
ここで、水深hの場所にある面が受ける圧力をPとすると、以下の関係式が成り立ちます。
$$PA=F_a+F_w=P_aA+\rho Ahg$$
両辺をAで割ると、
$$P=P_a+\rho hg$$
よって、水深hの物体が受ける圧力は、物体の面積には関係なく、水深hで決まることがわかります。

このことから冒頭で話してように「水中の物体は、水深が深いところにあるほど圧力を受ける」ということがわかりますね。
そのため、水深hの気泡が受ける水圧は、
$$P_a+\rho hg\cdots(1)$$
水面の気泡が受ける水圧は、h=0であることから、
$$P_a\cdots(2)$$
となります。
続いて、気体の状態変化を考えていきます。
一般的に、気体にかかる「圧力」が変化すると、気体の「体積」や「温度」が変化します。
しかし、今回は問題文で「気泡の温度はどの場所でも一定」と言っているので、等温変化とみなすことができます。
等温変化における気体の状態変化は、ボイルの法則より
$$PV=\rm{const.}$$
を使います(Vは気体の体積です)。

用語問題で、どっちがボイルの法則で、どっちがシャルルの法則なのかがよくごっちゃになりますよね。
ボイル(boil)は「沸騰」という意味ですが、「ボイルするときの温度は100度で一定」として、
「ボイルの法則」=「温度が一定」、「シャルルの法則」=「圧力が一定」
って覚えると良いと思います。
(厳密に言うとおかしいですが、あくまで覚え方の話です。)
水深hにある気泡の圧力をP1、体積をV1、
水面にある気泡の圧力をP2、体積をV2とすると
$$P_1 V_1 = P_2 V_2$$
$$V_2 = \frac{P_1}{P_2} V_1$$
となります。
ここで気泡は球形とみなせることから、
$$\frac{4}{3}\pi\left(\frac{d}{2}\right)^3 = \frac{P_1}{P_2}\frac{4}{3}\pi\left(\frac{d_0}{2}\right)^3$$
$$d^3=\frac{P_1}{P_2}d_0^3\cdots(3)$$
あとは(3)式に、(1)(2)式を代入して計算すれば求めることができます。
$$d^3=\frac{P_a+\rho_w hg}{P_a}d_0^3$$
$$d = \left(\frac{P_a+\rho_w hg}{P_a}\right)^{(1/3)}d_0$$
これが答えとなります。
厳密には深さhのところにある気泡と、水面近くの気泡との位置の差は、問題文の絵的には「h-(d/2)」ですが、
問題文で「気泡の直径は水深に比べて十分小さい」としているので、気泡の半径分のズレは無視してもOKです。
今回の問題のように、物体を「球」と見なす場合には「半径の3乗」、
また「立方体」と見なす場合には「一辺の長さの3乗」といったように、
「3乗」が出てきます。
そのため、体積から「半径」や「一辺の長さ」を求めるためには、「3乗根」を計算する必要があります。
かなり大きい数字はほとんど問題には出てきませんが、1〜9の数字の3乗ぐらいは覚えておいたほうが良いでしょう。
| 13 = 1 |
| 23 = 8 |
| 33 = 27 |
| 43 = 64 |
| 53 = 125 |
| 63 = 216 |
| 73 = 343 |
| 83 = 512 |
| 93 = 729 |
特に「343」が「7の3乗」であることには気づきにくいので、注意してください。
今回のポイントについてまとめると、以下の通りとなります。
今回は以上となります。ご一読、ありがとうございました。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

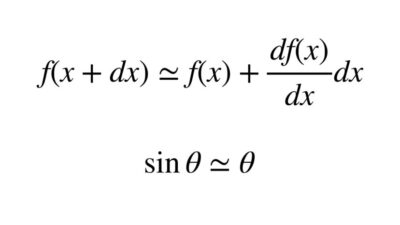
力学で出てくるテイラー展開と近似【式の導出でよく使います】
球殻を引き離す力の計算