自分で自分を持ち上げるのが不可能なことの証明【力学的に説明します】
メニュー
メニュー
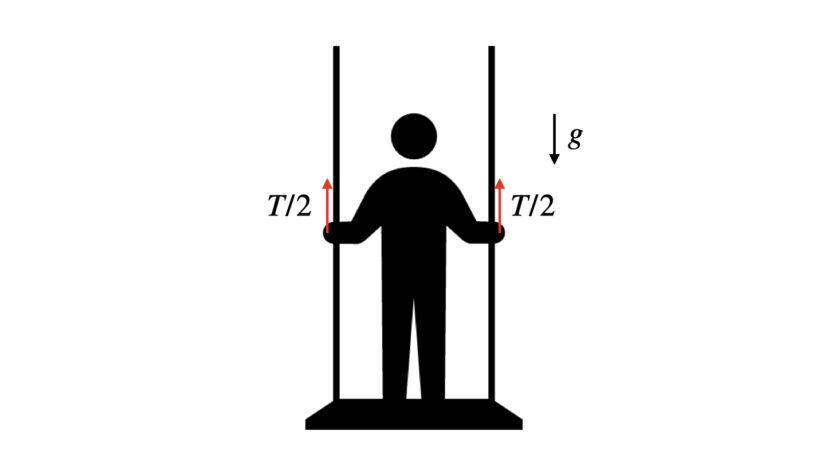
台の上に乗って、ジャンプと同時に台を上に引き上げたけど、宙に浮けない。まぁ、やる前から宙に受けないのはわかるけれど、物理現象として考えた時に、どうやったら証明できるのかな？
今回の記事では、高校物理の「力学」の問題について解説していきたいと思います。
力学の考え方が理解できているかどうかを問われている基礎的な内容で、期末テストでも普通に出題されるような問題ですので、自身のない人はしっかり理解するようにしていきましょう。
台の上に人が乗っている状況を考えます。台の上面には手で握れるように、取手がついていることとします。
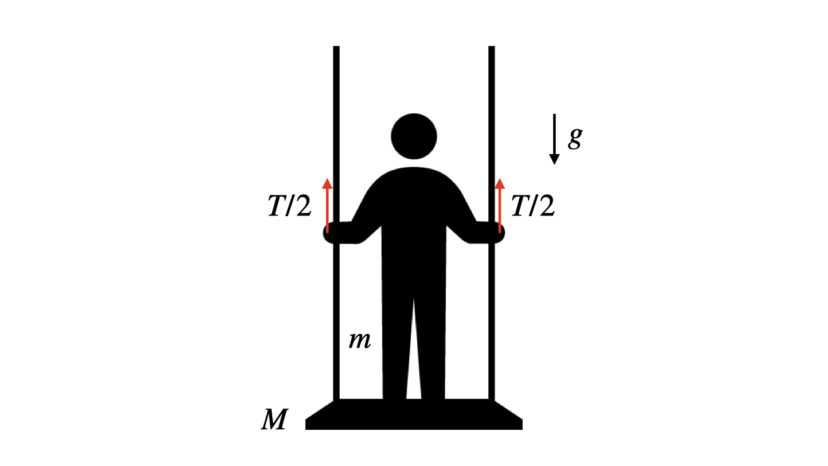
ここで、人の質量をm、台の質量をM、重力加速度をg、人が取っ手を上に引っ張る力を片手あたりT/2とします。
この取っ手を、台に乗っている人が上方向に引き上げた時、人は宙に浮くことができるでしょうか？
・・・というのは、みなさんのご想像のとおり、できません。
では「できない」ということを、式を使って証明してみましょう。
もし可能なら、少しの間記事を読むのをやめて、どのように証明したら良いのか考えてみてください。
解き方の方針ですが、「仮に宙に浮くことができる」と仮定して式展開をしていったとき、「物理的な矛盾がないか」をチェックします（つまり背理法です）。
まずは「人が受ける力」について考えていきます。
上向きを正とすると、以下のような関係になります。
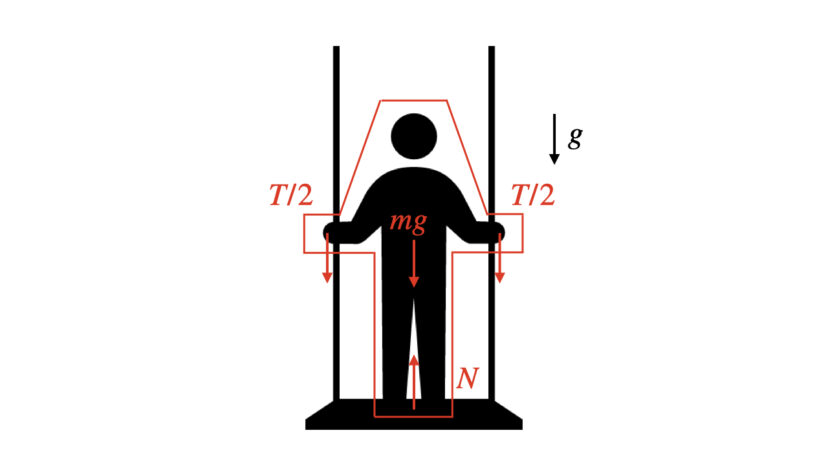
$$N-2\frac{T}{2}-mg=0\cdots(1)$$
Nは垂直抗力を表します。
ここでの注意は「-T/2」の部分です。
(1)式で表しているのは「人が受ける力（与えるではない）」なので、T/2の反力である「-T/2」となります。
今度は、台に関する力について考えて行きましょう。
力の方向に気をつけつつ、台がが受ける力について式を立てると、以下の通りとなります。
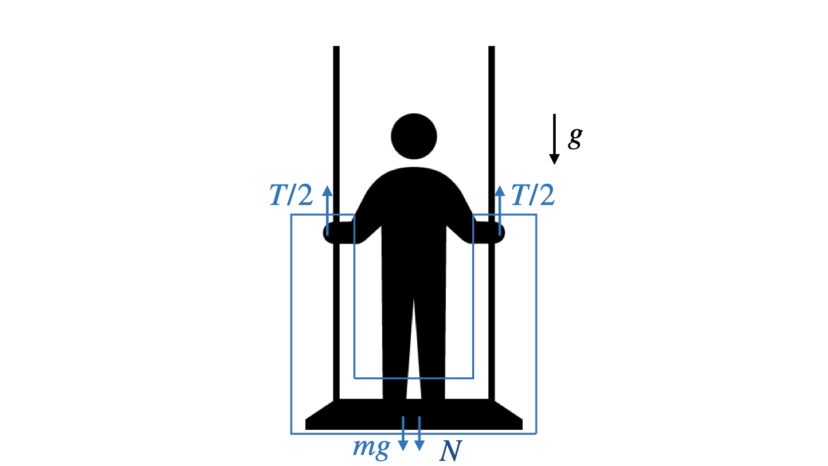
$$2\frac{T}{2}-N-Mg=0\cdots(2)$$
では(1)(2)式で連立方程式を立てて解いていきます。
$$\begin{cases} \displaystyle N-2\frac{T}{2}-mg=0\cdots(1)\\
\displaystyle 2\frac{T}{2}-N-Mg=0\cdots(2)\end{cases}$$
(1)式より、
$$N=T+mg\cdots(3)$$
(3)式を(2)式に代入すると、以下のようになります。
$$2\frac{T}{2}-(T+mg)-Mg=0\\m=-M\cdots(4)$$
この(4)式が、宙に浮くための条件となります。
この(4)式から言えることは、次の2つです。
取手を上に引っ張る力T/2は、(1)式、(2)式で登場しましたが、連立方程式を解く段階で、消去されてしまっています。
そのため、マッチョな人がどれだけ大きな力で引っ張ろうとも、宙に浮くためには意味をなさないと言うことが言えます。
(4)式を成り立たせるには、人または台のどちらかの質量がマイナス、または人および台の質量が0である必要があります。
人も台も、質量が0以下になることはありえません。
しかし、現実的にそのようなことはありえないので、自分で自分を持ち上げることは負荷能なのです。
人が乗っている台をひとが直接持ち上げることはできません。しかし、滑車の力を借りれば、持ち上げることができます。
台にワイヤーを取り付け、滑車を通じて人がワイヤーを下に引張っているとします。
ワイヤーの重さがないと仮定し、その状態で宙に浮いている（釣り合っている）と仮定すると、人が受ける力は下の図のような関係となります。
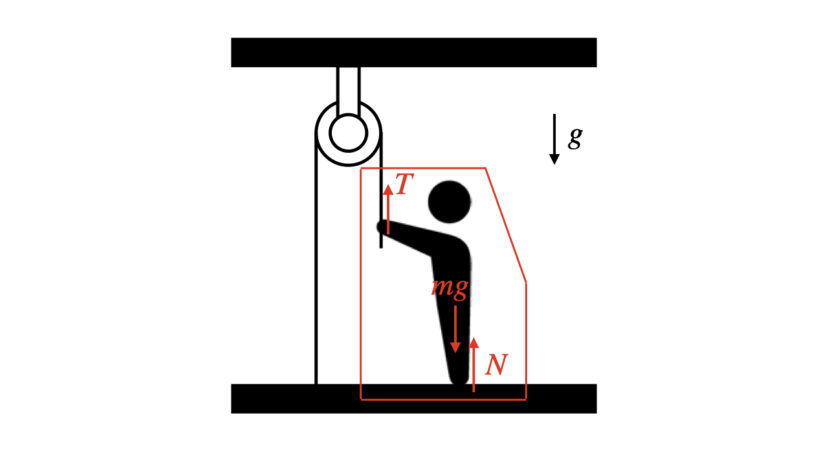
$$N+T-mg=0\cdots(5)$$
(1)式と(5)式との違いは、Tの符号です。つまり、滑車を取り付けたことによって、力を受ける方向が180度変わったということになります。
一方、台が受ける力は(2)式と同じになります。
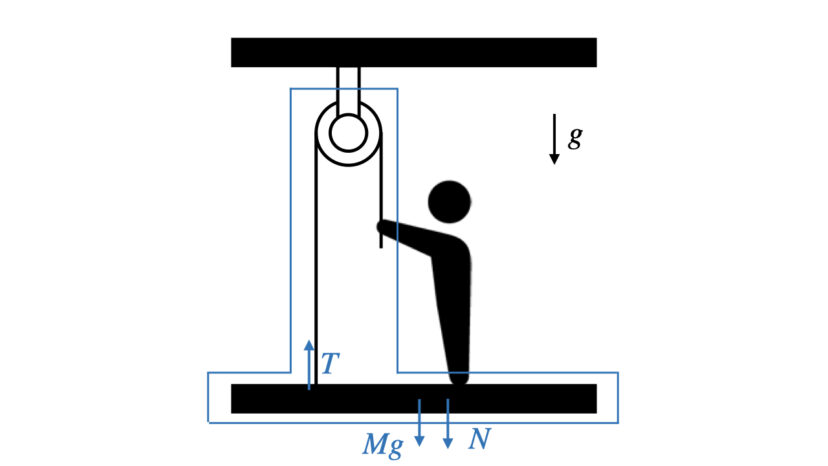
$$T-N-Mg=0\cdots(2)$$
これらを連立方程式として立てて解くと
$$\begin{cases}T-N-Mg=0\cdots(2)\\N+T-mg=0\cdots(4)
\end{cases}$$
(5)式より、
$$N=mg-T\cdots(6)$$
(6)式を(2)式に代入すると、
$$T-(mg-T)-Mg=0\\2T=(m+M)g\\T=\frac{(m+M)g}{2}$$
これが答えとなります。ただし、実際には完全に宙に浮いている訳ではなく、滑車が取り付けられている天井が(m+M)gの力を受けているということになります。
いかがだったでしょうか。
このような背理法を使った証明問題は、割と鉄板なのでぜひ身につけておくようにしましょう。
なお、今回のような高校物理的な問題については、以下の参考書でわかりやすく説明されています。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。
機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...
斜面と斜面に垂直方向以外への、力の分解方法【物理】
ばねの直列・並列の現象について
