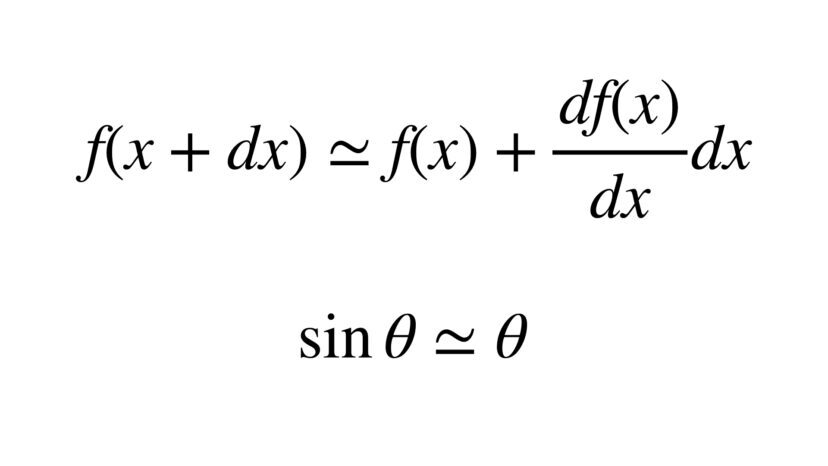
大学の工学・力学の授業で、いろんな式の導出を習っているけれど、特に「微小な値」とか「十分に小さい」とか言って、いきなり式が近似されるのがイマイチ納得できない。
このような疑問・悩みを持った人へ、お答えしていきます。
力学を学ぶと、「微小な要素を考える」とか「〜が十分小さい」という言葉がたくさんでてきます。
このような言葉が出来たあとには、ほとんどのケースで近似が行われます。
いくつか例を挙げると、以下の科目では間違いなく登場します。
式の近似が行われるとき、実は「テイラー展開」と「微小な値」という条件が組み合わさってできています。
しかし、この式変換は力学であまりにもよく登場するためか、生徒が質問をしない限り、テイラー展開であることすら教えてくれないことが多いです。
そのため、この近似の工程にイマイチ納得ができないという方も多いのではないでしょうか。
「こういうものだ」と思考停止で受け入れれば、直近の定期テストなどには対応できるかもしれませんが、自分の中で納得ができていないと、すぐ忘れるし、モチベーションも下がります。
そこで今回は、力学でよく出てくるテイラー展開と近似について納得していただけるよう、お話していきます。
テイラー展開とは一言でいうと「ある関数f(x)の特定の範囲(点aの近傍)に限って、f(x)を微分したものの和を使ってほぼ等しくなるように表したもの」となります。
もう少しわかりやすくいうと、「f(x)を微分したもの」を「○+○+○+・・・」というふうに何個もつなぎ合わせる事によって、点aの周りに限ってf(x)っぽい関数を作るということです。
関数f(x)を、x=a周りでテイラー展開すると、以下のようになります。
$$f(x)=f(a)+\frac{df(x)}{dx}(x-a)+\frac{1}{2!}\frac{d^2f(x)}{dx^2}(x-a)^2+\cdots\hspace{40pt}(1)$$
これだけ見ると、足し算が無限に続くから逆に複雑になったように見えるかもしれませんが、
後述するように「微小」や「十分に小さい」などと言った情報と組み合わせることによって、元の関数を非常にシンプルな形で表すことができるのです。
力学を勉強していると、以下のような近似式がよく出てきます。
そのときに、以下のような式をよく目にするはずです。
$$f(x+dx)\simeq f(x)+\frac{df(x)}{dx}dx$$
この式は、dxが微小である場合にf(x+dx)をx周りでテイラー展開し、近似した結果なのです。
その導出について、以下に詳しく解説します。
まずテイラー展開は(1)式ですが、x=x+dx、a=xであるとし、式に当てはめますと
$$\begin{align}f(x+dx)&=f(x)+\frac{df(x)}{dx}(x+dx-x)+\frac{1}{2!}\frac{d^2f(x)}{dx^2}(x+dx-x)^2\cdots\\
&=f(x)+\frac{df(x)}{dx}dx+\frac{1}{2!}\frac{d^2f(x)}{dx^2}dx^2\cdots\hspace{40pt}(2)\end{align}$$
となります。ここでポイントなのが「dxは微小量である」ということです。
微小量であると何ができるかというと、微小量が2乗、3乗・・・などとされているものは、0とみなすことができます。
例えば、dx=0.01の場合、(dx)2=0.0001ですし、(dx)3=0.000001です。
そのため、計算したとしても、全体に及ぼす影響がほとんどないのです。
すると(2)式は以下のように近似されるのです。
$$\begin{align}f(x+dx)\simeq f(x)+\frac{df(x)}{dx}dx\end{align}\hspace{40pt}(3)$$
以上が、近似式の導出となります。
特に高校物理の振り子問題では、以下のような式をよく目にするはずです。
θが十分に小さい時、
$$\sin\theta\simeq\theta$$
高校生の頃は「そういうものだ」というふうに教えられた人もいるかと思います(というか、私がそうでした)が、この近似ができる理由についてお話します。
この近似式は、sinθという関数を、「θ=0周りでテイラー展開をしたもの」から出てきます。
(1)式でいう、x=θ、a=0とみなしてテイラー展開すると、以下のようになります。
$$\sin\theta=\sin(0)+\frac{d\sin\theta}{d\theta}(\theta-0)+\frac{1}{2!}\frac{d^2\sin\theta}{d\theta^2}(\theta-0)^2\cdots\hspace{40pt}(4)$$
ここでθが十分に小さい時(このθの単位はラジアンです)、先ほどの例と同様で、θが2乗、3乗・・・などとされているものは、0とみなすことができます。
よって、(4)式は以下のように近似することができます。
$$\begin{align}\sin\theta&\simeq\sin(0)+\frac{d\sin\theta}{d\theta}(\theta-0)\\
&=0+(\cos\theta)\cdot\theta\hspace{40pt}(5)\end{align}$$
ここで1つポイントがあります。
「cos(0)=1」ですので、θが十分に小さい時は「cosθ≒1」と近似することができます
よって、(5)式は以下のように近似されます。
$$\begin{align}\sin\theta&\simeq0+1\cdot\theta=\theta\end{align}$$
以上が近似式の導出となります。
力学ではf(x,y,z)といったように、変数が3つある場合も多く登場します。
そこから、x、y、z方向にそれぞれ少しだけ移動した点、f(x+dx,y+dy,z+dz)のテイラー展開は以下の通りとなります。
$$\begin{align}
f(x+dx, y+dy, z+dz)=&f(x,y,z)\\
&+\left(dx\frac{\partial}{\partial x}+dy\frac{\partial}{\partial y}+dz\frac{\partial}{\partial z}\right)f(x,y,z)\\
&+\frac{1}{2!}\left(dx\frac{\partial}{\partial x}+dy\frac{\partial}{\partial y}+dz\frac{\partial}{\partial z}\right)^2f(x,y,z)\\
&+\frac{1}{3!}\left(dx\frac{\partial}{\partial x}+dy\frac{\partial}{\partial y}+dz\frac{\partial}{\partial z}\right)^3f(x,y,z)\cdots
\end{align}$$
このテイラー展開ができれば、あとは「微小」とか「十分に小さい」というキーワードから近似を行えば、式をシンプルにすることができます。
今回のポイントについてまとめると、以下の通りとなります。
力学・工学系の人は、この記事の内容を知っておくだけでほぼ十分ぐらいですが、テイラー展開についてもう少し詳しく知りたい方は、以下の書籍をご参考ください。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

ばねの直列・並列の現象について
気泡の大きさの計算方法