ラプラス変換表

ラプラス変換とは

ラプラス変換は、よく制御やメカトロニクスの分野で登場するものです。

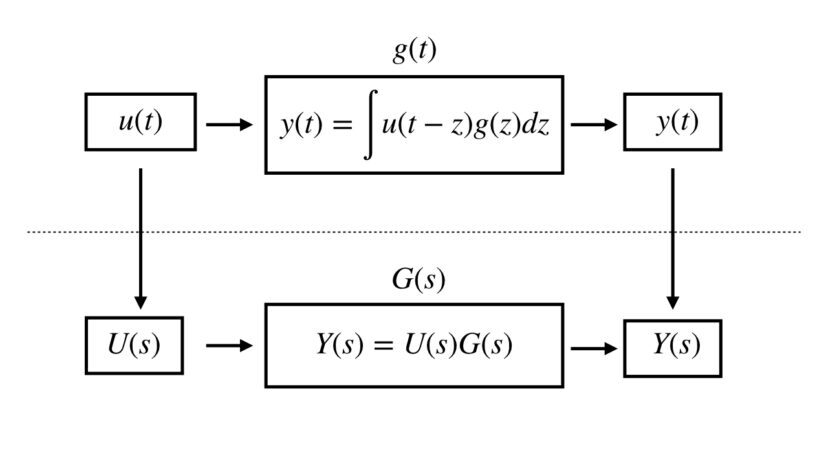
あるシステムについて、ブラックボックス化している「システムの中身g(t)」を調べるために、「サンプルとなる信号」入力して、それによって出力された信号との関係性から求めるのですが、

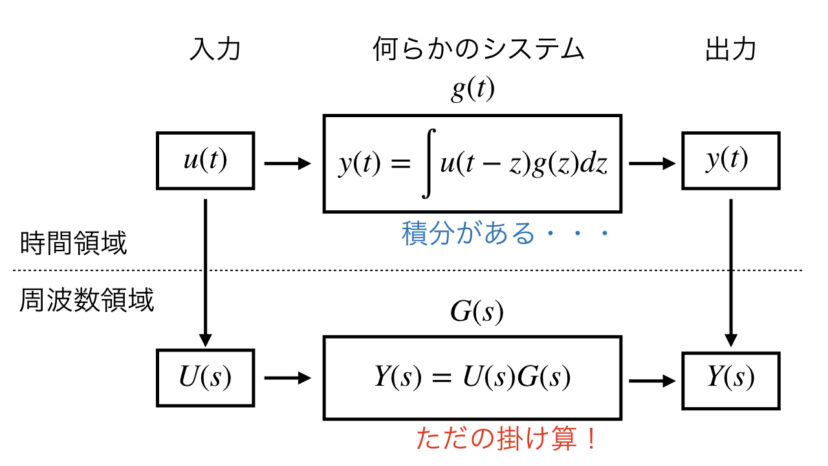
時間領域では積分（たたみ込み積分といいます）をする必要があって、非常に面倒くさいです。

そこで、ラプラス変換をすることによって、「積分の部分がただの掛け算になる」というメリットが有り、非常に便利なのです。

ラプラス変換は一応定義があるのですが、それよりも「ラプラス変換表」という表を見ながら変換するのが一般的ですので、以下の表をご参考にしていただければと思います。

時間領域 $f (t)$	周波数領域 $F (s)$
$\frac{d f}{d t}$	$s F$
$\int f d t$	$\frac{F}{s}$
$a f_{1} + b f_{2}$	$a F_{1} + b F_{1}$
$δ (t)$	$1$
$1$	$\frac{1}{s}$
$t$	$\frac{1}{s^{2}}$
$e^{- a t}$	$\frac{1}{s + a}$
$\sin a t$	$\frac{a}{s^{2} + a^{2}}$
$\cos a t$	$\frac{s}{s^{2} + a^{2}}$
$e^{- a t} \sin b t$	$\frac{b}{(s + a)^{2} + b^{2}}$
$e^{- a t} \cos b t$	$\frac{s + a}{(s + a)^{2} + b^{2}}$
$t^{n} e^{- a t}$	$\frac{n!}{(s + a)^{n + 1}}$
$\frac{1}{b - a} (e^{- a t} - e^{- b t})$	$\frac{1}{(s + a) (s + b)}$
$\frac{1}{s q r t 1 - ζ^{2}} e^{- ζ ω_{n} t} \sin ω_{n} \sqrt{1 - ζ^{2}} t$	$\frac{ω_{n}}{s^{2} + 2 ζ ω_{n} s + ω_{n}^{2}}$

ちなみに、ラプラス変換の定義は以下のとおりですが、ぶっちゃけほとんど使わないです・・・

ラプラス変換

$F (s) = \int_{0}^{\infty} f (t) e^{- s t} d t$

逆ラプラス変換

$f (t) = \frac{1}{2 π j} \int_{c - j \infty}^{c + j \infty} F (s) e^{s t} d s$

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

この記事を書いた人

機械設計エンジニア: りびぃ

極座標と直交座標の使い道【一言でいうとモンストとパズドラです】