高校数学で、今までずっとxy座標でやってきたのに、いきなり極座標とかいって、rやθが出てきて、わけがわからん。極座標なんて何の役に立つの?
このような疑問・悩みを持った人へ、お答えしていきます。
「座標」や「グラフ」は、中学の数学で初めてが登場しますが、このときに習うグラフはx軸とy軸とが直角に交わるようになっているグラフです。
このような座標系を「直交座標系(またはデカルト座標系)」と呼びます。
一方で、高校数学の数Ⅲでは、ある位置を表す別の方法として、rやθを用いた「極座標系」を習います。
これは、原点からの距離と、角度とで表したグラフです。
ですが、極座標を習うときには唐突に「こういうのを極座標というので、覚えましょう」といった具合に登場してくるので、
「x座標とy座標とで表せばいいグラフを、なんでわざわざ面倒くさそうな極座標で表さなきゃいけないのか。」
「極座標って一体何の役に立つのか」
といったことを、あまりじっくりは教えてくれません。
ですが極座標は状況によっては非常に有効な座標系であるどころか、xy座標なんかでやろうとすると逆に計算が複雑化してしまう場合があります。
私は大学・大学院では機械系の専門でしたが、xy座標と同じぐらいの頻度で極座標を授業で取り扱っておりました。
そこで今回は、極座標とはどのような座標なのか、どのような 場面で役に立つのか、という使い道についてお話していきます。
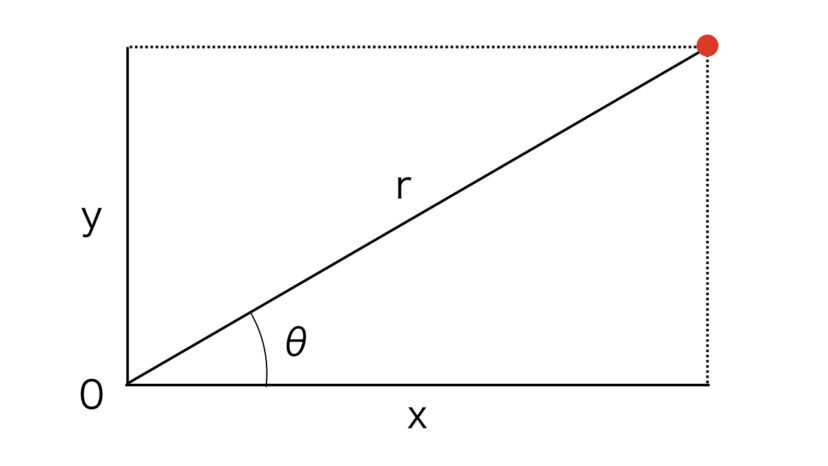
極座標とは、原点からの距離(r)と角度(θ)とを使って座標を表す方法(座標系)です。
ある位置(場所)をr、θ座標で表すということは、「中心から、半径方向に〇〇、角度が〇〇」といった感じでに表すということです。
この極座標は「モンスト(モンスターストライク)」を想像していただけるとわかりやすいです。
モンストは、味方のモンスターを発射し、敵へ当てて倒していきますが、敵モンスターへ狙いを定めるときに、極座標が使われています。
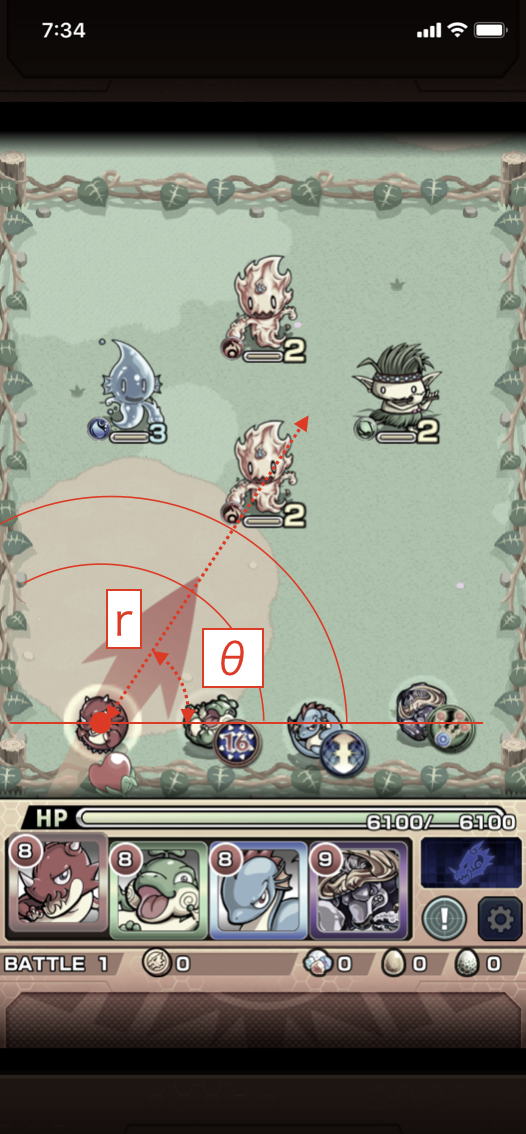
モンスターを思いっきり引っ張ることによって、「r座標」が大きくなり、発射する強さを大きくできますし、
発射角度を調整することによって、「θ座標」が変動し、敵に狙いを定めることができます。
これにより、モンスターで敵を狙う際に「人間の直感どおり」に狙うことができます。
このように極座標は、円にちなんだものに対して使用することで、非常に便利となるのです。
ちなみにθはラジアンですので、注意をしてください。
一方で中学校などで習った直交座標(デカルト座標)は、「横方向に〇〇、縦方向に〇〇」といった感じで表すもので、一般的にはx軸、y軸を用いて使用します。
この直交座標は「パズドラ(パズル&ドラゴンズ)」を想像していただけるとわかりやすいです。
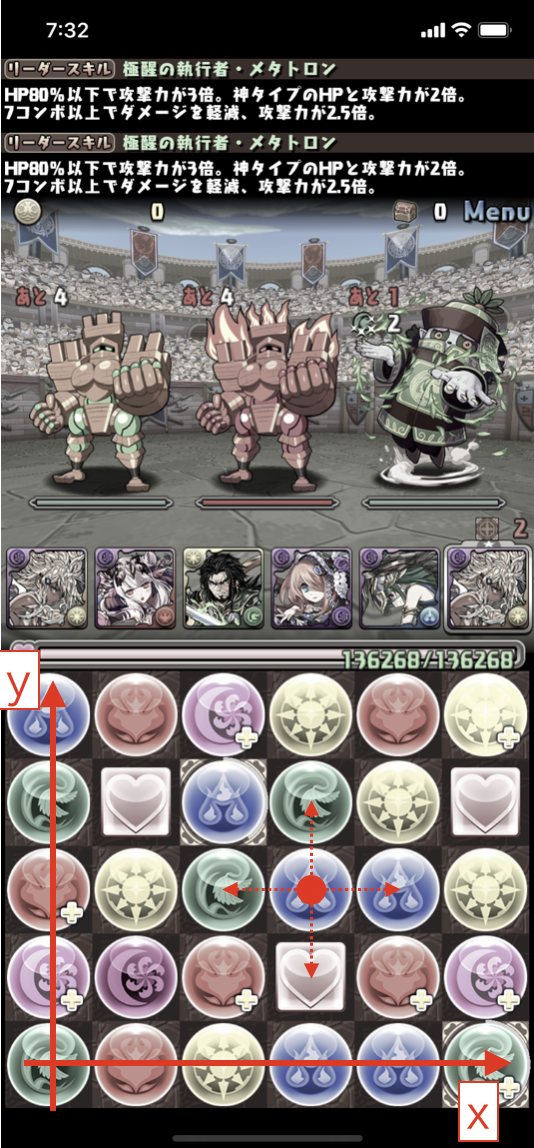
パズドラは通常、縦5つ、横6つに並んだドロップの一つを指で選択し、縦や横方向に動かすことでパズルを解いていきます。
そして、縦または横に3つ以上同じ色が揃うとドロップを消すことができ、攻撃や回復を行うことができます。
このようにパズドラは、縦・横方向を基本とするので、直交座標との相性がいいのです。
極座標のイメージとして「モンスト」を取り上げましたが、実際に社会ではどのように役立っているかを説明します。
私は機械系の学問を専攻していたので、それを例にあげますが、
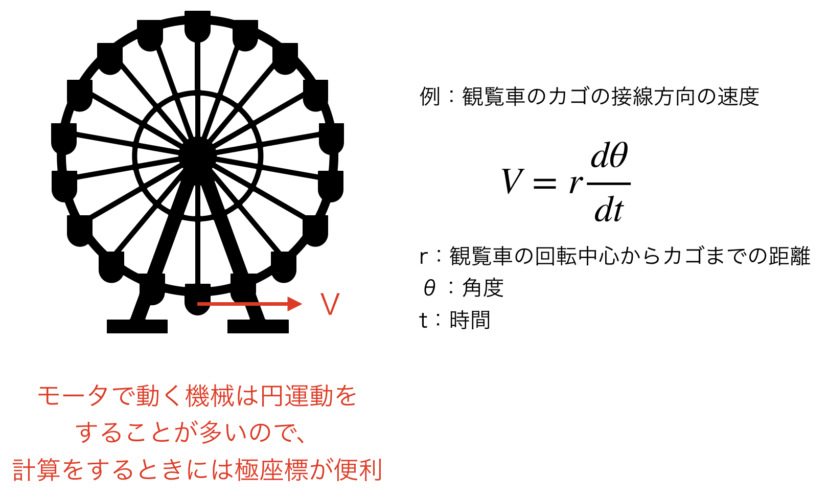
例えば「モータに関する計算」をするときに極座標は便利です。
今の社会では、ほとんどの機械にモータが使われておりますが、モータによって回転する軸は円運動ですので、極座標と相性がいいのです。
極座標も直交座標も、座標の表現方法が異なるだけで、「座標が表す場所そのもの」は何も変わりません。
そのため、英語が日本語に訳すことができるように、極座標を直交座標で、または直交座標を極座標で表すことができるのです。
極座標を直交座標へ変換するには、以下の式を使います。
$$\begin{align} \begin{cases} x=r \cos\theta\cdots(1)\\ y=r \sin\theta\cdots(2) \end{cases} \end{align}$$
何やら三角関数が出てきましたが、これは三角関数の定義から簡単に導けます。
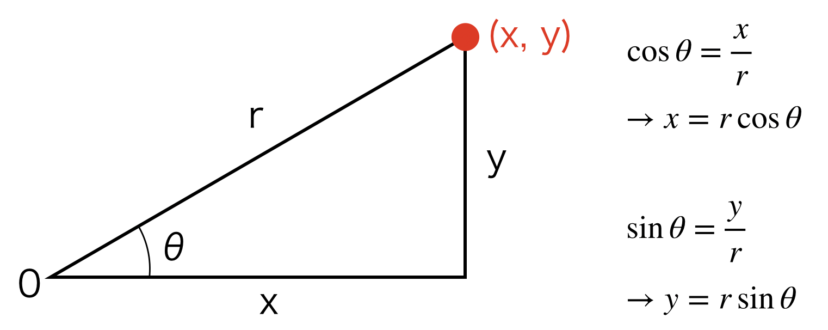
人によっては、以下の図の方が覚えやすいかもしれません(私はこっちで覚えました)
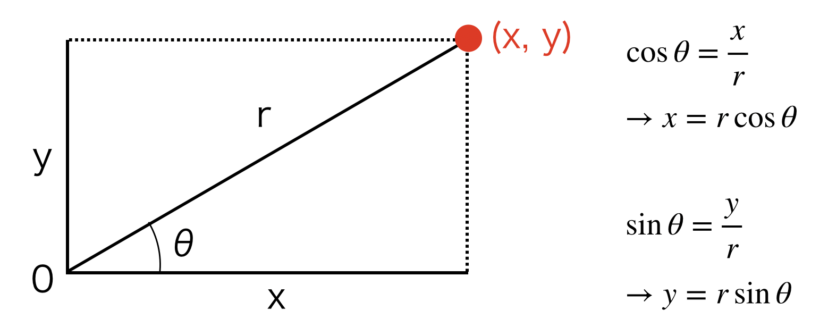
先ほどとは逆に、直交座標から極座標へ変換するには、以下の式を使います。
$$\begin{align} \begin{cases} r=\sqrt{x^2+y^2}\cdots(3)\\ \theta=\tan^{-1}\frac{x}{y}\cdots(4) \end{cases} \end{align}$$
この式は、三平方(ピタゴラス)の定理、およびタンジェントの逆関数で求めることになります。
なお、直交座標を極座標へ変換するのに、(1)式や(2)式は使えないことに注意してください。
極座標への変換で「r=」「θ=」の形にしようとしたときに、(1)式や(2)式では、右辺に「r」または「θ」が残ってしまうのです。
右辺で使える変数は「x」と「y」だけなので、三平方(ピタゴラス)の定理、およびタンジェントの逆関数で求めるようにしてください。

今回のポイントについてまとめると、以下のとおりとなります。
なお、受験対策などのために極座標をマスターしたいという方は、チャート式で勉強するのがいいかとおもます。
また、ラジアンの扱いについてあまり慣れないという方は、以下の記事が参考になるかと思います。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

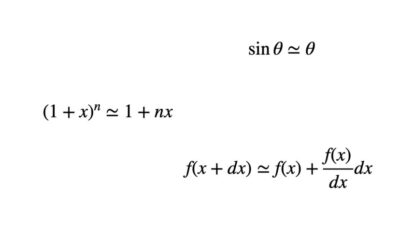
【解説】機械工学系の学問でよく使う近似式
ラプラス変換表