斜面と斜面に垂直方向以外への、力の分解方法【物理】
メニュー
メニュー
以前、斜面上に置かれた物体に働く摩擦力を計算する方法を説明しました。
【問題】
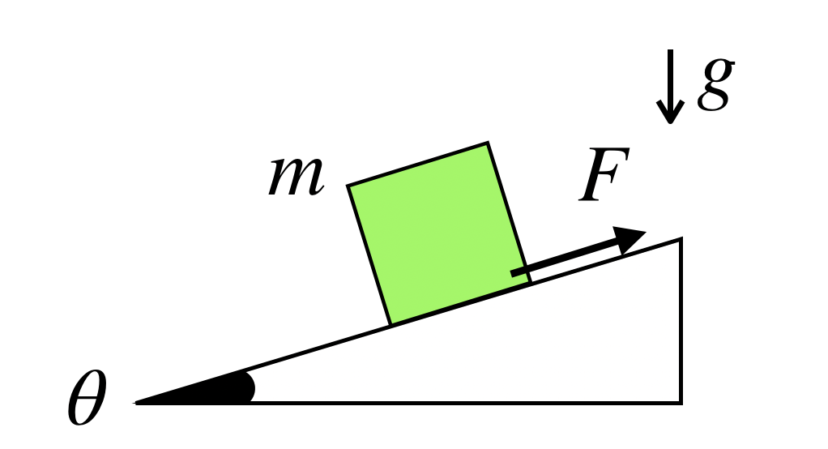
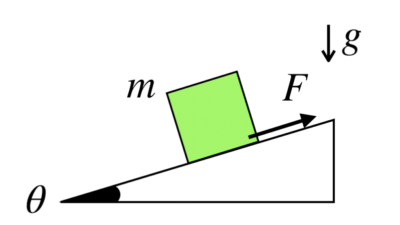
摩擦力の働く斜面の上に物体を置きます。物体が静止しているとき、物体に働く摩擦力の大きさFを求めてください。
物理の問題を解く上では、座標軸を設定して、その座標軸に合うように要素を分解します。
この座標の設定方法については、基本的には問題を解く人の自由です。
しかし、設定した座標軸によって、問題を解く難易度は変わります。
基本的には、座標を分解するのは以下のいずれか、または両方を満たすように座標軸を揃えるのがオススメです。
では、それ以外の方法で問題を解くとどうなるか、なぜオススメではないのかについてお話ししていきます。
少しだけ計算が煩雑にはなりますが、水平方向と垂直方向へ分解して、式を立てることは、不可能ではありません。
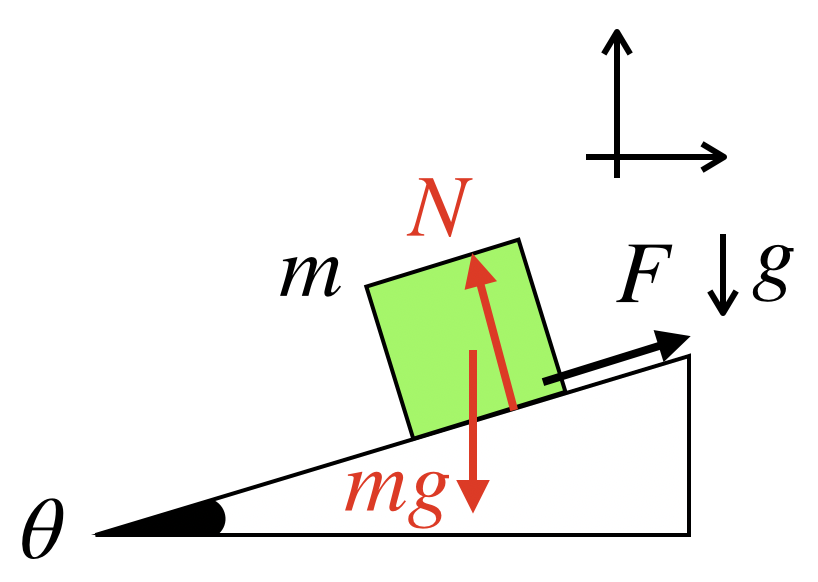
では、実際にやってみます。
この場合、mgは分解をする必要がありませんので、NとFについて分解を行います。
ところで、下図のように、三角形と三角関数との関係をみてみますと、NやFは三角形の斜辺に相当します。
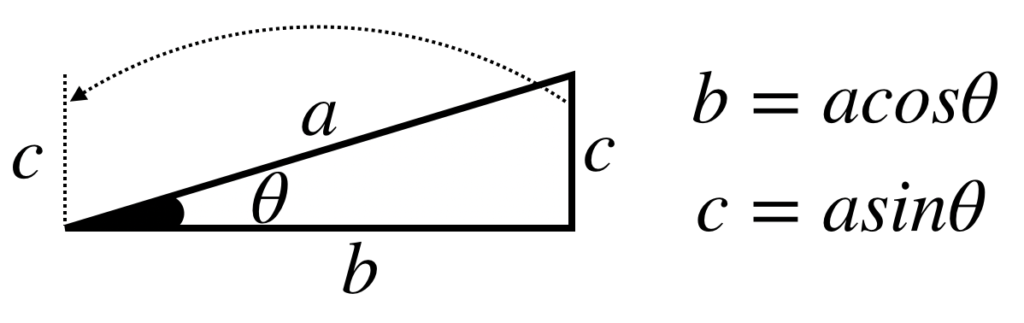
よって、NやFを分解しますと、以下のようになります。
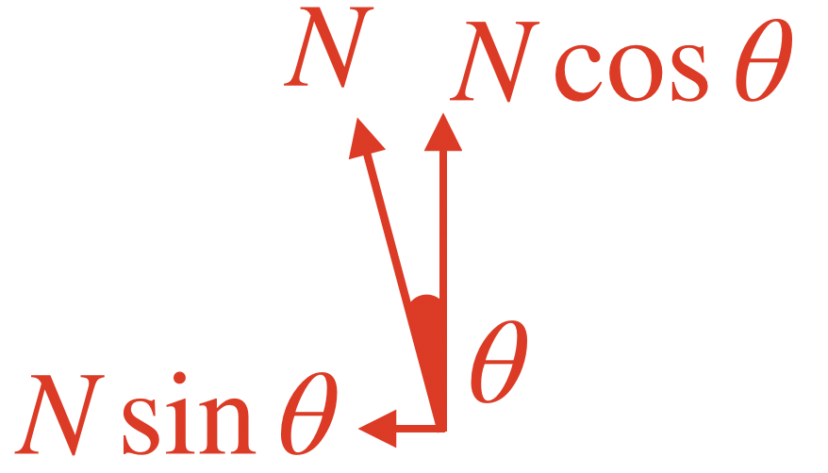
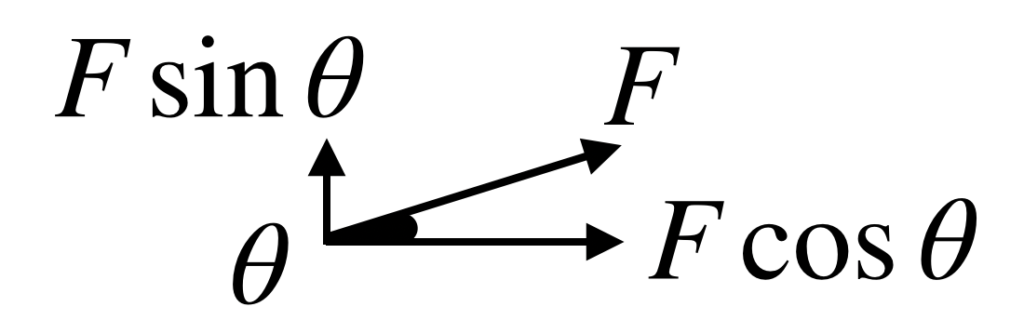
よって、式を立てますと、以下のとおりとなります。
$$\begin{cases}
F\cos\theta-Nsin\theta=0\cdots(1)\\
N\cos\theta-mg=0\cdots(2)
\end{cases}$$
(1)式に、今回の問題で求められているFがありますが、Nが未知数であるため、(1)式だけでは解くことができません。
そのため、(1)(2)式を使った連立方程式を解く必要があります。
斜面方向と、斜面に垂直な方向に分解した時と比べて、計算に時間がかかりますので、オススメはしません。
今までは、分解された後のベクトルが直角になるように分解を行なっていました。
しかしベクトルの分解方法は任意ですので、直角になるように分解をしなくてもよいのです。
たとえば、斜面方向と重力方向になるようにベクトルを分解してもよいのです。
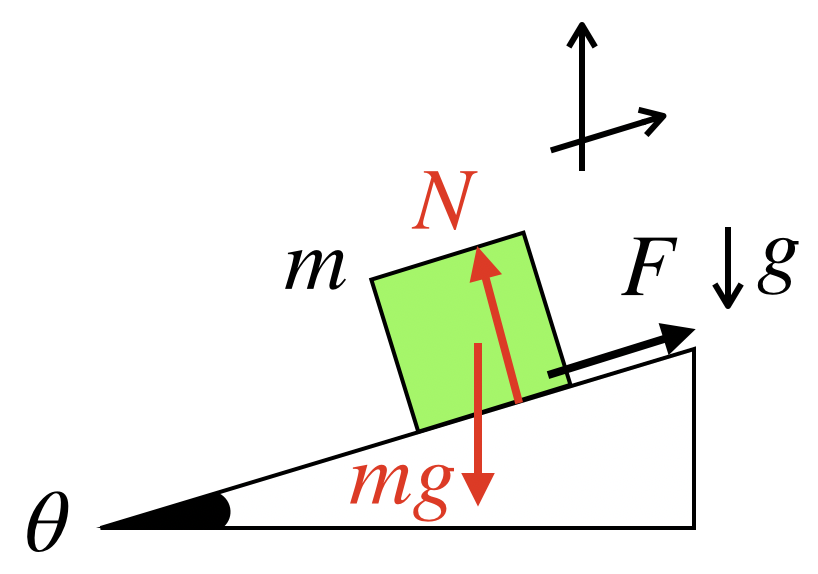
それでは、実際にやってみます。
mgとFについては分解をする必要がないので、この場合、分解の対象になるのは、垂直抗力Nです。
以下に三角形と、三角関数の関係図を示しますが、この図で言うとNは辺bに相当します。
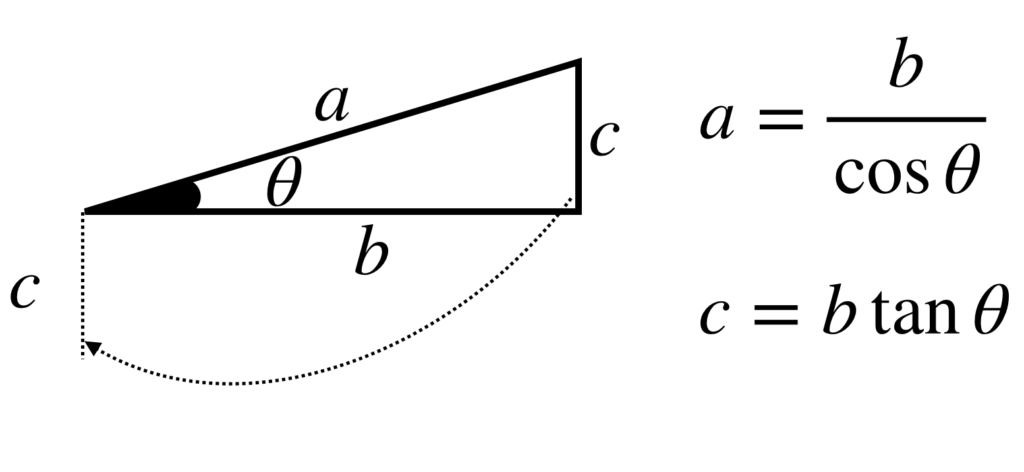
よって、Nを分解すると、下の図のようになります。
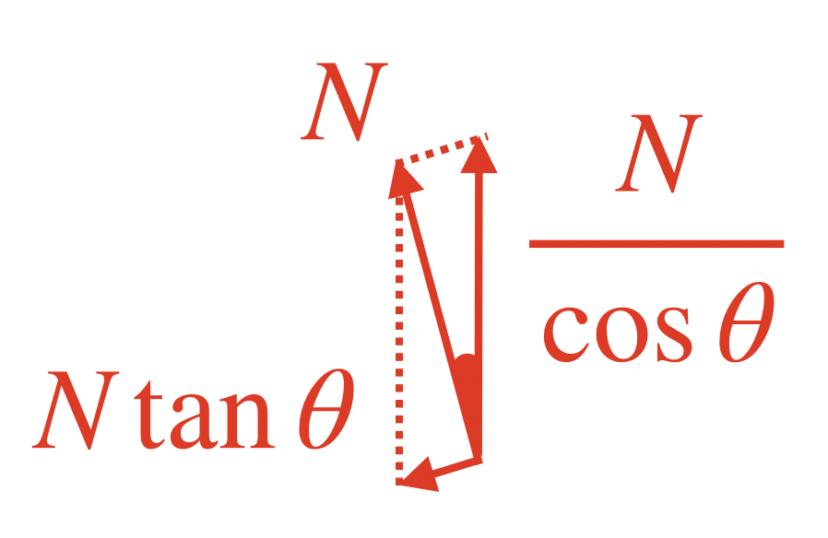
よって、方程式を立てると、以下のようになります。
$$\begin{cases}
\begin{align}
F-N\tan\theta\cdots(3)\\
mg-\frac{N}{\cos\theta}=0\cdots(4)
\end{align}
\end{cases}$$
こちらの方法でも、(3)(4)式を使った連立方程式を解く必要があります。
このように、教科書通りにベクトルを分解しなくても計算はできるのですが、明らかに複雑になるため、オススメはしません。
なお今回の記事は、こちらの書籍を参考にさせていただきました。
冒頭でお話ししたオススメの分解方法については、以下の記事で解説しておりますので、こちらをご覧ください。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。
機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...
斜面に静止している物体の問題の解き方のコツ【物理】
自分で自分を持ち上げるのが不可能なことの証明【力学的に説明します】
