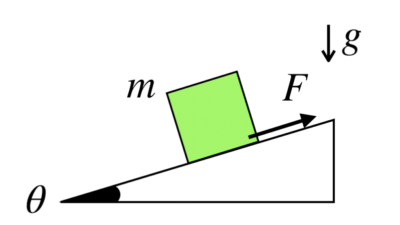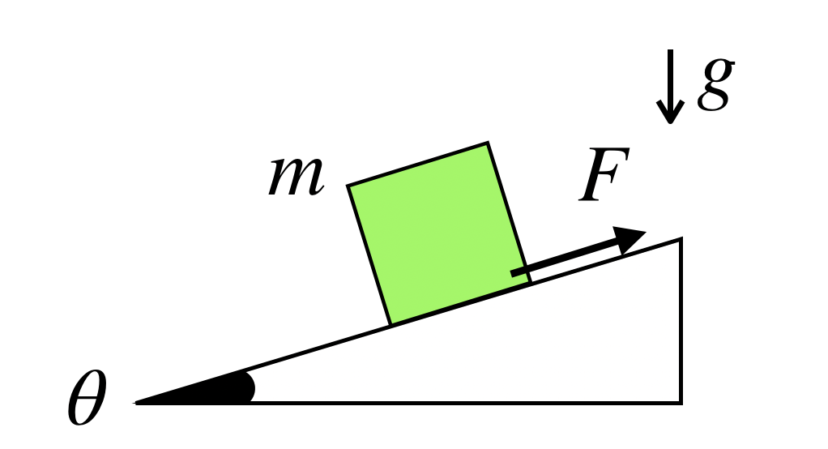
今回は、高校物理を勉強し始めたばかりの人のための、力学の話をします。
高校物理で力学の勉強をすると、ほとんどの教科書や参考書に、以下のような問題が掲載されております
【問題】
摩擦力の働く斜面の上に物体を置きます。物体が静止しているとき、物体に働く摩擦力の大きさFを求めてください。
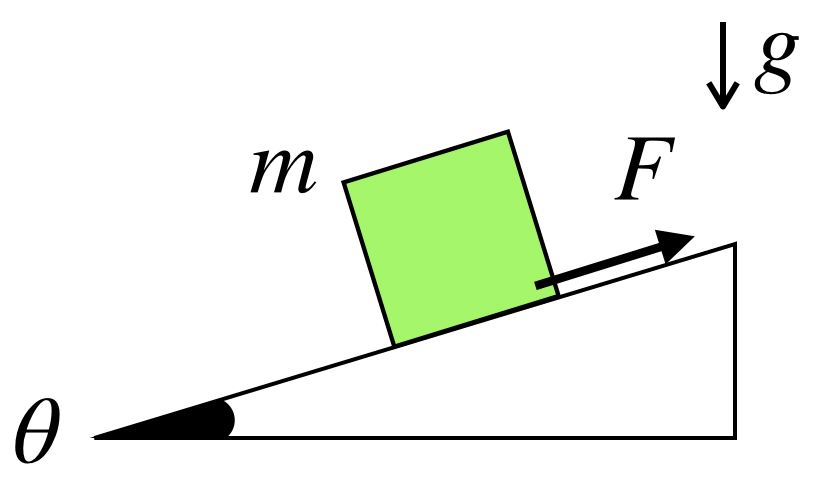
非常にシンプルなつりあいの問題ではありますが、力学の問題を解く上での基本がたくさん詰まった問題となります。
今回は、この問題を通じて、解き方の流れや座標軸の設定方法、ベクトルの分解方法のコツについてお話しします。
基本的に釣り合いの問題を解く流れとしては、以下の通りとなります。
まずは、物体が受ける力を考えていきます。
物体に働く力には大きく分けて以下の二種類があります。
場から受ける力は基本的に「重力場から受ける力」「電場から受ける力」「磁場から受ける力」の3種類しかありませんが、
今回の問題で関係するのは「重力場から受ける力」です(重力加速度が作用していますので)。
「重力場から受ける力」は、重力加速度が作用している方向に、(物体の質量)×(重力加速度) の大きさで作用します。
続いて、触れているものから受ける力について、今回の問題で斜面上の物体が触れているのは、斜面そのものなので、この斜面から力を受けます(物体が斜面から力を受けていないと、物体は斜面にめり込んでいくことになります)。
「作用、反作用の法則」により、物体は斜面から「垂直抗力」を受けますので、とりあえずNとおいて、図示します。
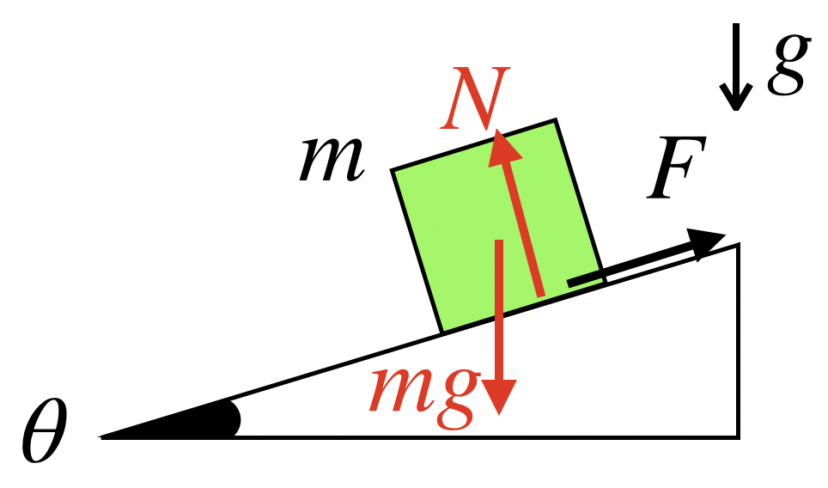
続いて、座標軸を設定する方法ですが、以下の2つのコツのどちらかに従って設定することをおすすめします。
座標軸の設定については、どのように座標軸を設定するかは皆さんの自由です。
しかし、設定した座標軸によって、問題を解く難易度が変わることがよくあります。
先ほどご紹介したコツを今回の問題に当てはめると、斜面に沿った方向と、斜面に垂直な方向との座標軸を考えるのが、適切となります。
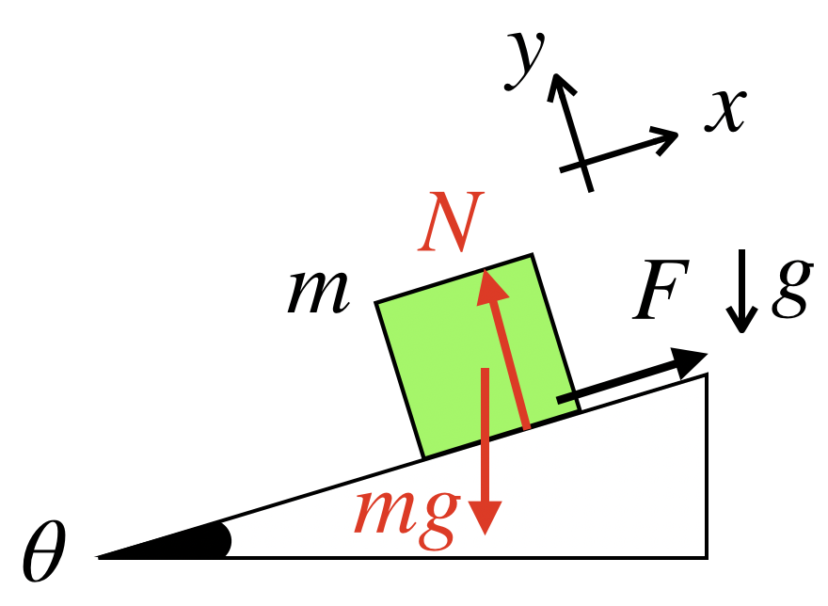
座標軸に沿って、力を分解します。
垂直抗力Nは、すでに座標軸に沿った方向になっていますので、ここでは物体が受ける重力を分解していきます。
ベクトルを分解するには三角関数を使用していきます。
多くの問題において、分解する前のベクトルが、三角形の斜辺に相当しますので、斜辺にsinやcosをかけることによって、分解をすることができます。
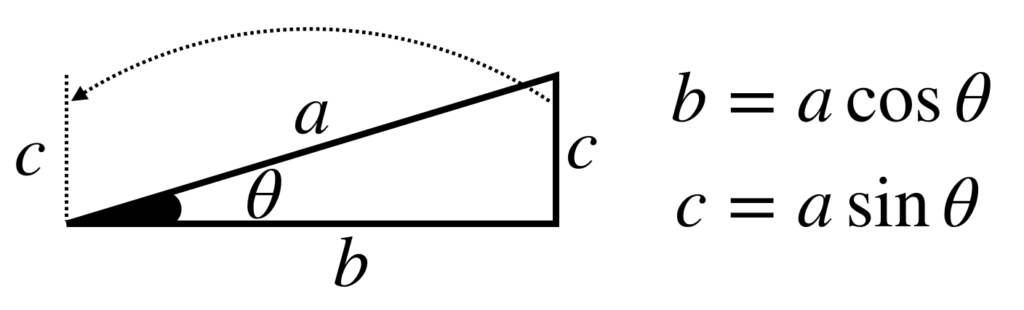
よって、今回の問題の場合では、以下のようになります。
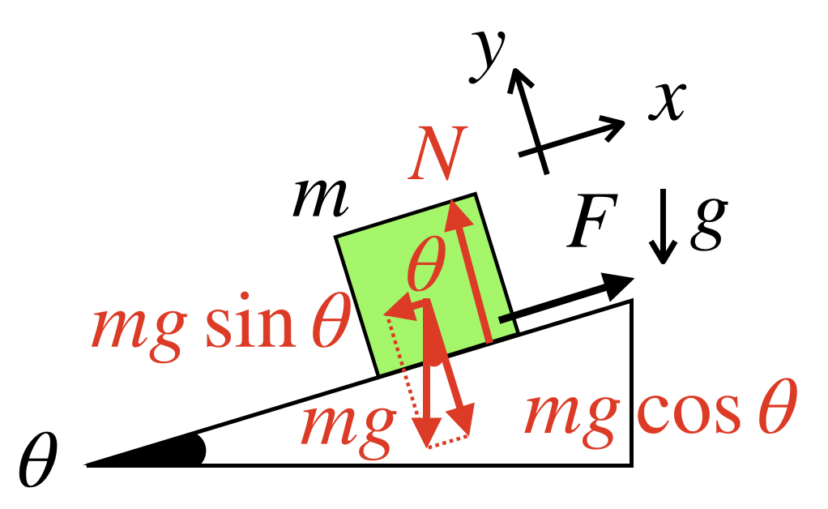
斜面の傾斜θがどこの角度と等しいか、わからなくなるという人は、θを思いっきり大きくしたり、小さくしてみたりして絵を書いてみてください。
そうすると、傾斜θと等しい角度が把握しやすくなります。
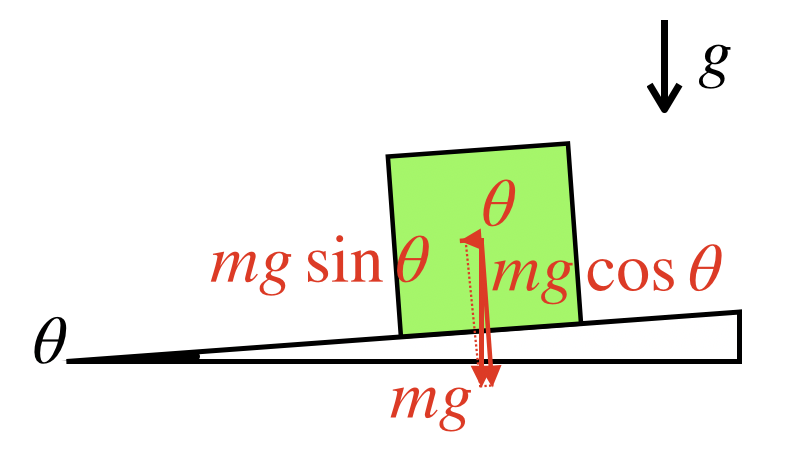
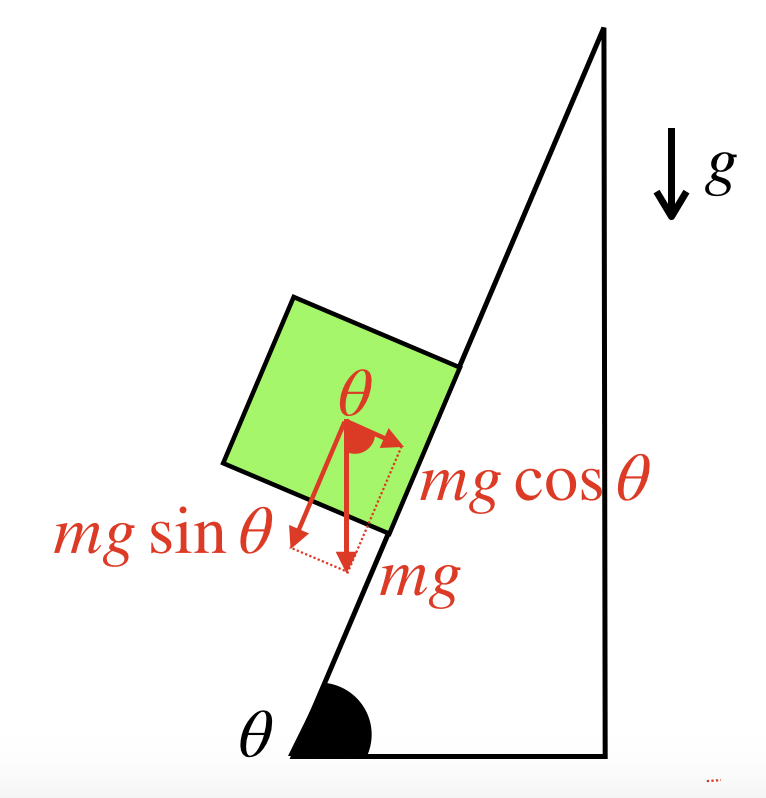
ここまでいけば、あとは釣り合いの式を立てればOKです。x軸方向、y軸方向それぞれの方向で、式を立てます。
$$\begin{cases}
\begin{align}
F-mg\sin\theta=0\cdots(1)\\
N-mg\cos\theta=0\cdots(2)
\end{align}
\end{cases}$$
今回求めるのは、摩擦力Fですが’(1)には未知数が1つ(F)しかありませんので、(1)だけを使えば問題が解けます。
よって答えは、
$$F=mg\sin\theta$$
となります。
もう少し色々な問題を解いてみたいという人は、こちらの書籍がおすすめです。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

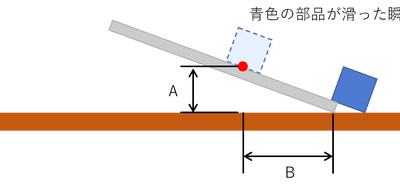
高校生でも理解できる!静止摩擦係数の測定原理
斜面と斜面に垂直方向以外への、力の分解方法【物理】