こんにちは!リヴィと申します!
普段は機械設計者として、日本のものづくりに貢献する仕事をしております。
この記事を読むべき人
材料力学という学問は、以下の2つの項目について取り扱う学問です。
この内、(1)については「応力」という指標を使います。
応力には「垂直応力」と「せん断応力」という2種類が存在し、それらを使って評価します。(詳細について以下の記事をご参照ください▼)
今回は、(2)の「変形」を評価する上で必要な「ひずみ」についてお話してきます。
応力にも種類があったように、ひずみにも「〇〇ひずみ」という種類が存在します。
以前話をした「応力」に種類があったように、実は「ひずみ」にも種類があります。
その2種類とはズバリ「垂直ひずみ」と「せん断ひずみ」です。「垂直応力」や「せん断応力」とセットにして覚えておくと良いです。

「あれ?さっきの『応力』の部分が『ひずみ』に変わっただけやん!」って思いますよね笑。そう、そのとおりです。
言葉だけではなく、中身までイメージそのまま。
垂直応力によって発生したひずみが「垂直ひずみ」、せん断応力によって発生したひずみが「せん断ひずみ」です。
用語も中身も似ているので、ひずみの種類については応力とセットで覚えるのがおすすめです。
イメージを掴むだけであればこれで終了なのですが、「じゃあ今からひずみの問題を説いてください。」と言われると、なかなかペンが進まなかったりします。
それは、ざっくりとした概念は簡単ですが、ちゃんと定義や数式まで学習しようとすると、少しとっつきにくい部分があるからです。
そこで今回はこれらひずみの種類について、詳しく解説していきたいと思います。
今回の記事を読めば、イメージを掴むだけではなく、数式を使って解けるようになれるので、ぜひ最後までご一読ください。
材料を仮想断面や、微小要素に区切ったとき、その面に対して垂直方向に発生するひずみのことを「垂直ひずみ」と言います(仮想断面や微小要素については、応力の種類の記事内で解説しております。)。
垂直ひずみの定義式は以下のとおりです。
$$垂直ひずみ=\frac{変形後の材料の長さ-元の材料の長さ}{元の材料の長さ}=\frac{材料の変形量}{元の材料の長さ}$$
この「材料の長さ」というのは、「仮想断面や微小要素で区切ったところまでの長さ」という場合もありますし、「材料全体の長さ」という場合もあります。
ただ、基礎の範囲では後者の「材料全体の長さ」で考える問題が比較的多いです。
垂直ひずみは一般的に「ε(イプシロン)」という記号を使って表します。
数式にすると以下のとおりです。
$$\varepsilon=\frac{L-L_0}{L_0}=\frac{\Delta L}{L_0}$$
| $$\varepsilon$$ | 垂直ひずみ | [-] |
| $$L$$ | 変形後の材料の長さ | [mm] |
| $$L_0$$ | 元の材料の長さ | [mm] |
| $$\Delta L$$ | 材料の変形量 | [mm] |
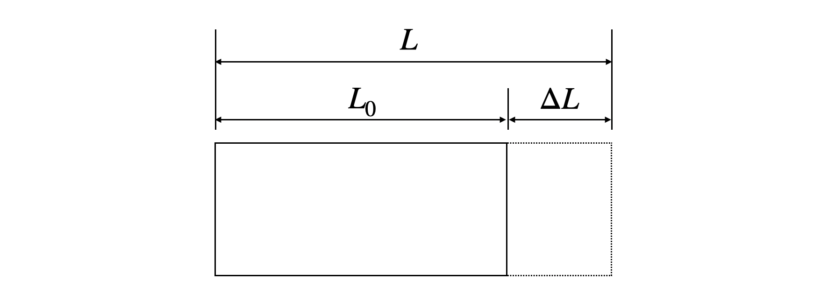
上の式の通り、材料の変形量の表し方には2通りの方法があります。
1つ目は、変形後の長さから変形前の長さを引き算する方法、2つ目は変形量そのものを使う方法です。
大学の期末テストの問題においては、どちらの式を使うかは五分五分なので、両方とも覚えておくと良いです。

なお応力と同様に、引張方向に発生するひずみを引張ひずみ、圧縮方向に発生するひずみを圧縮ひずみと言います。ひずみが0のときが変形がない状態、プラスのときは引張ひずみ(伸びている状態)、マイナスのときは圧縮ひずみ(縮んでいる状態)となります。
ちなみに、ひずみは「変形の割合を示すもの」ですので、この式に「×100」をするとパーセント表示することができます。
$$\varepsilon=\frac{\Delta L}{L_0}\times100 [\%]$$
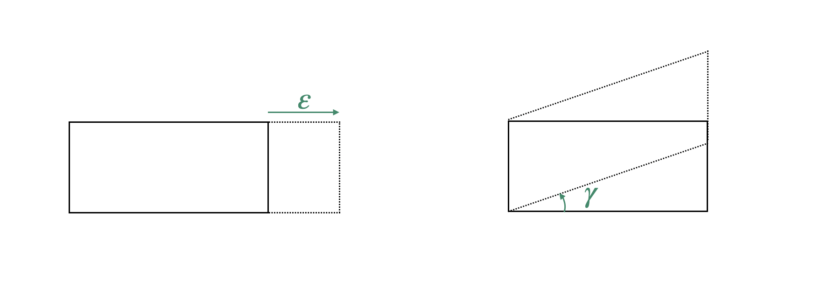
材料を仮想断面や、微小要素に区切ったとき、仮想断面に対して平行に発生するひずみを、「せん断ひずみ」といいます。
せん断ひずみが発生すると、材料は平行四辺形の形に変形します。
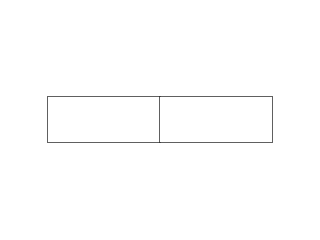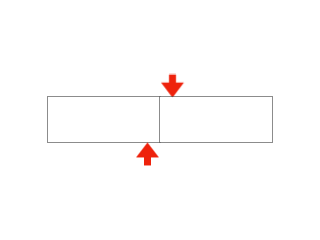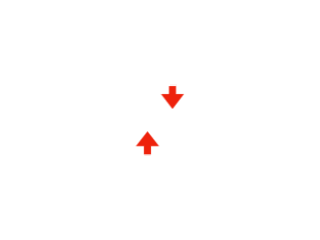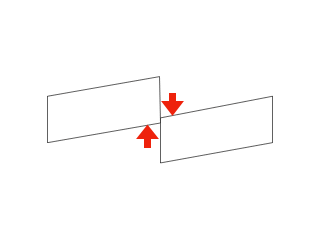
せん断ひずみの定義式は以下のとおりです。
$$せん断ひずみ=\frac{材料の変形量}{元の材料の長さ}$$
せん断ひずみは一般的に「γ(ガンマ)」という記号を使って表します。
数式にすると以下のとおりです。
$$\gamma=\frac{\Delta L}{L_0}$$
| $$\gamma$$ | せん断ひずみ | [-] |
| $$L_0$$: | 元の材料の長さ | [mm] |
| $$\Delta L$$ | 材料の変形量 | [mm] |
ちなみに、ここでいう「材料の変形量」とは、せん断応力の発生している方向の変形量です。
垂直ひずみとは異なるので注意をしましょう。
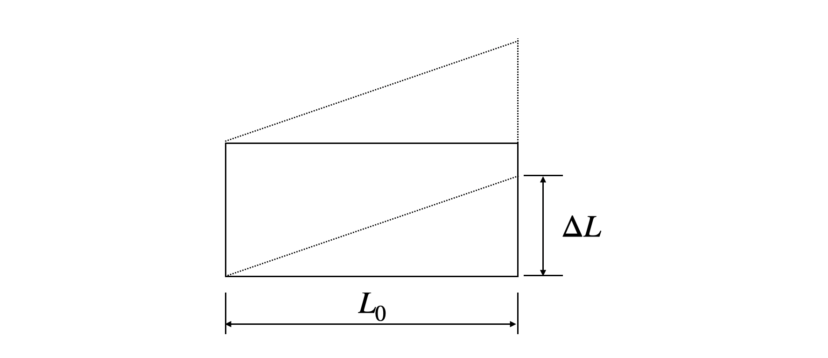
なお、せん断ひずみは角度を使っても表すことができます。(高校数学の三角関数の知識が必要です)
例えば、材料がせん断荷重を受けたことによって、下図のように
材料の角度がπ/2からφへ変形したとします。(角度は「度」ではなく、「ラジアン」です)
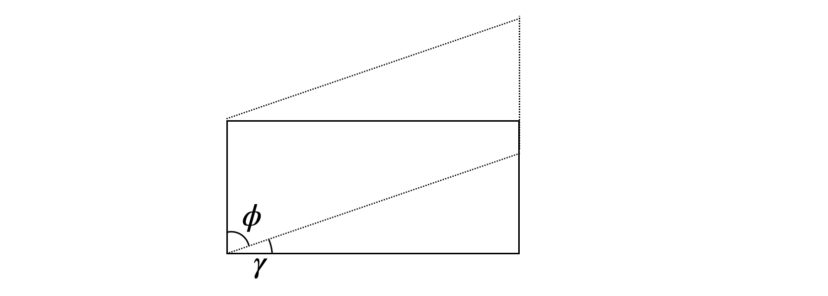
これを式で表すと、このようになります。
$$\frac{\pi}{2} – \phi= \gamma \cdots(1)$$
| $$\phi$$ | 変形後の角度 | [rad] |
| $$\gamma$$ | 角度の変化量 | [rad] |
長さを使った表現とは、式の形が異なりますが、実はほぼ同じ値になることが証明できます。
それは以下の通りです。
長さを使って表したせん断ひずみγは以下の通りでした。
$$\tan\gamma = \frac{\Delta L}{L_0} \cdots(2)$$
ここで、角度の変化量γが微小であるとき、以下の近似式が成立します。
$$\tan\gamma\simeq \gamma\cdots(3)$$
よって、(1)(2)(3)より、以下の関係が成立します。
$$\frac{\pi}{2} – \phi= \gamma=\tan\gamma = \frac{\Delta L}{L_0}$$
よって、角度の変化量が微小であるならば、せん断ひずみを、長さで表した場合でも、角度で表した場合でも同じ値になることがわかります。

「角度の変化量γが微小であるとき」と言いましたが、材料力学においてγが30°とか45°などととてつもなく大きくなるケースはほぼ扱いません。γに対するtanγの誤差については、10°のときにtanγの方が1%大きくなる程度です。
ひずみは割合を示すものですが、割合の計算には注意しなければならないことがあります。
例えば、まず長さ100mmの棒を引張って5%ひずませ、その後さらに引張って5%ひずませるとします。このとき、元の形状に対してのひずみはいくつになるでしょうか。
このとき、「5%+5%=10%」と答えたら間違いです。
確かにはじめに5%ひずませると、100mm×1.05=105mmとなります。
ですが、その後さらに5%ひずませると、105mm×1.05=110.25mmとなるので、答えは10.25%です。

小中学校の算数の、食塩水の問題が苦手な人が多いように、割合を使った計算を苦手とする人は多いです。しっかりと身に付けたいものですね。
今回の内容についてまとめると、以下の通りとなります。
今回は以上となります。ご一読ありがとうございました。
続きの記事はこちら▼
高校の数学とか物理とかめちゃくちゃ苦手なレベルな人向け書籍▼
高校の数学・物理はある程度できる人向け書籍▼
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

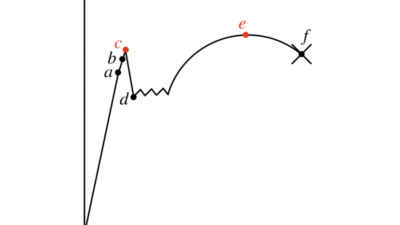
材料力学の本質:応力とひずみの関係
応力ひずみ線図の読み方のポイント
