材料は荷重を受けると、材料に応力が発生し、さらにひずみが発生します。
つまり、「応力」と「ひずみ」には関係性があります。
これらの関係についてグラフで表したものを、応力-ひずみ線図と呼びます。
応力-ひずみ線図とは、材料力学という学問の本質である
「材料がどの程度変形するか」
「材料が壊れるかどうか」という命題に答えるグラフです。
応力-ひずみ線図は、材料の材質(鉄とかアルミとか)によって、グラフの形状が異なりますが、同じ材質であれば、ほぼ同じ形状のグラフとなります。
そんな応力-ひずみ線図についての入門的な内容を、今回は解説していきます。
まずは、グラフを見ていきましょう。
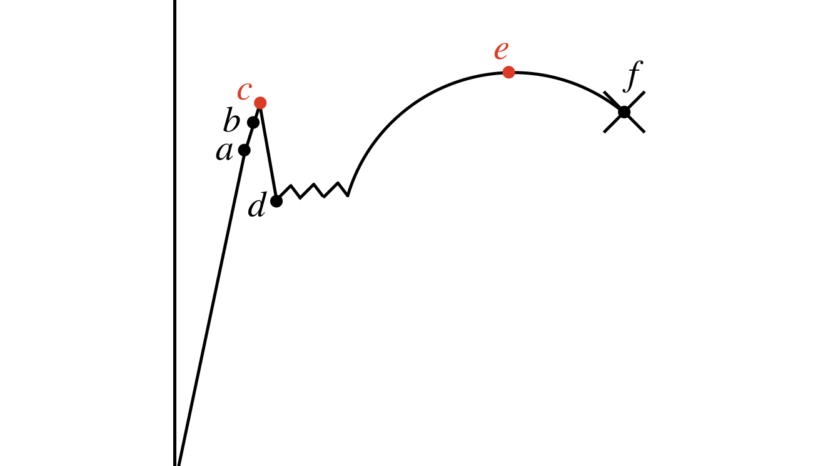
下のグラフは、多くの教科書や参考書に記載されている「軟鋼の引張りの応力-ひずみ線図」です。
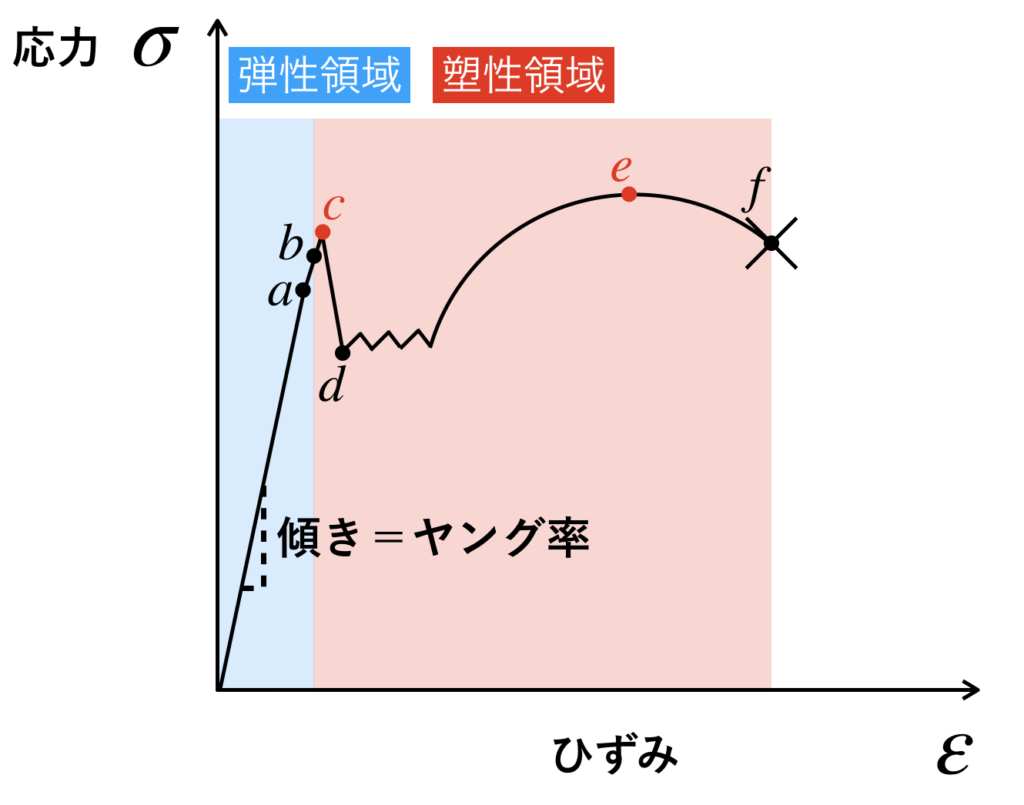
応力-ひずみ線図には、そのグラフの要所に名前がついております。
特に赤で示した、「降伏応力」「引張強さ」は、部品の強度計算で使う非常に重要な応力値です。
弾性限界から左側の領域を弾性領域、弾性限界から右側の領域を塑性領域といいます。
弾性領域では、材料に与えた荷重を0の状態にすると、ひずみが0、つまり荷重がかかっていない元の形状に戻ります。
基本的にものづくりにおける設計では、材料に荷重が加わったときに発生する応力がこの弾性領域内を超えないように、材質や形状などを決定します。
塑性限界では、材料に与えた荷重を0の状態にしても、ひずみが0にならない、つまり永久変形が生じます。
ただし、荷重を0にしても、全く元に戻らないというわけではなく、ある程度は元に戻ろうとします。
この現象をスプリングバックといい、曲げ加工(プレス機で曲げる加工方法)において重要な現象です。
ちなみに、たまに弾性領域と塑性領域との境目は、上降伏点といっているのを見かけますが、これは誤りです。
弾性領域のなかでも、ひずみが0の状態から比例限度までの領域では、「ひずみ」と「応力」とが比例の関係を示します。
この時のグラフの傾き(比例定数)をヤング率(縦弾性係数)といい、Eという記号で表します。
この関係を式にすると以下のようになり、これをフックの法則と呼びます。
[mathjax]
$$\sigma = E \varepsilon$$
ちなみに、応力の単位は[N/mm2]、ひずみの単位はないので、
ヤング率の単位は[N/mm2]です。
このヤング率の数値は、材質ごとに値が決まっております。
軟鋼の場合は、だいたい206,000 N/mm2です。
このヤング率のイメージですが、
「ヤング率の値が大きいほど、少しひずませるだけでも、多くの応力が必要」という風に見ることができるため、
ヤング率が大きい材料=硬い材料
ということになります。
材料力学の参考書などをみると、多くの場合「軟鋼の応力-ひずみ線図」が例として掲載されております。
ただし、ここで重要なのは、
「応力-ひずみ線図は材質が異なれば、グラフの形状も全く異なる」ということです。
そもそも、この「軟鋼」とは何なのか?
まず、鉄の中に炭素が入っている材料を「炭素鋼」と呼びます。
鉄には、炭素の含有量が多いほど硬くなるという性質がありますが、
そのなかでも、「炭素」の含有量が少ないものを「軟鋼」といいます。
この軟鋼は、鉄骨や、鉄道のレールなど、多種多様に用いられている材料です。世の中にかなり普及しているため、参考書にも多く登場するのだと思われます。
あまりにも多くの資料に「軟鋼の応力-ひずみ線図」が掲載されているため、
まるでどの材料にも、このような特性があるものだと、学生当時の私は思っておりましたが、
「降伏をした後の、グラフがギザギザになる特性がない材料」や、
「そもそも降伏しない材料」もあります。
この応力-ひずみ線図は「あくまで代表例である」ということに気をつけてください。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


材料力学 演習問題 01【応力】
材料に発生するひずみの種類【応力とセットで覚えよう】
