こんにちは!リヴィと申します!
普段は機械設計の仕事をしており、日本のものづくりに携わっております。
この記事を読むべき人
材料力学という学問は「(1)材料に力が加わった時、壊れないかどうか」「(2)材料がどの程度変形するか」を主として取り扱っていくものです。
ここで「材料に力が加わった時」とありますが、材料に力が加わる形態というのは、全部で5つあり「引張」「圧縮」「せん断」「曲げ」「ねじれ」となります(詳しくは以下の記事で解説しています)。
「よし。じゃあ、この5種類の中から荷重を判断して、材料の耐久性的なものと比べればいいのね!」
と思った方は、ちょっと待ってください!笑
イメージ的には合っているのですが、結論を言うとは荷重そのものではなく、「応力」と「ひずみ」というものを使って評価します。

たぶん、材料力学を勉強しない限りはほぼ聞かない用語だと思います笑。
でも実は、この「応力」と「ひずみ」というものは材料力学で1番大事なものと言っても決して過言ではなく、基礎だろうが応用だろうが、材料を評価するために必ずこれらを使います。
逆に、「応力」と「ひずみ」がわからないと、基礎問題すら解くのが難しくなります。
これは「インターネットのつなぎ方がわからないと、YouTubeを見たり、友達とLINEしたり、Amazonで買い物したりできない」というようなレベルのものです。
そこで今回は、「応力」や「ひずみ」というものは一体どういうものなのかについて、解説してきたいと思います。
今回の記事の内容がわかると、材料力学で出題される問題の解き方が大筋わかるようになりますので、是非最後までご覧ください。
めちゃくちゃザックリいうと、応力は「材料にかかる負荷を評価する時に使うもの」、ひずみは「材料の変形を評価する時に使うもの」となります。
そのため冒頭でお話したような、「永久変形したり、壊れたりするかどうか」に応力を使って、「どれだけ変形するか」にひずみを使うといったイメージを持っていただければOKです。
では、もう少しだけ詳しく「応力」と「ひずみ」について解説します。
応力の定義はズバり「単位面積あたりの内力」です。
$$応力=\frac{内力}{断面形状に関する値}$$
内力とはその文字の通り「材料の内部に発生する力」のことです。

あえて「断面形状に関する値」という言葉を使っていますが、わかりやすく言うと断面積などが挙げられます。ただし、断面積で計算しないパターン(断面係数という値を使います)もあるため、「断面形状に関する値」という言葉を使っております。
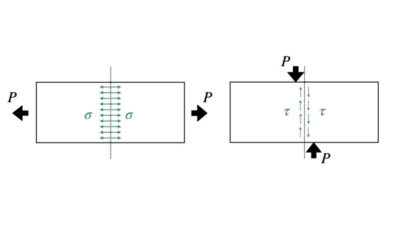
どういうことかというと、例えば物体に荷重(外力)が釣り合うように作用した時、
高校物理の範囲「外力は釣り合っている」という結論で終了していました。
ところが材料力学においては「外力が材料を介して釣り合いの関係にあるということは、材料内部では外力に持ちこたえるような抵抗力が働いている」と考えます。
下の右側の図でいうと、点線の位置で材料内部について考えた時、赤矢印の外力Pに対する抵抗力が赤矢印の力F、青矢印の外力Pに対する抵抗力が青矢印の力F、ということになります。
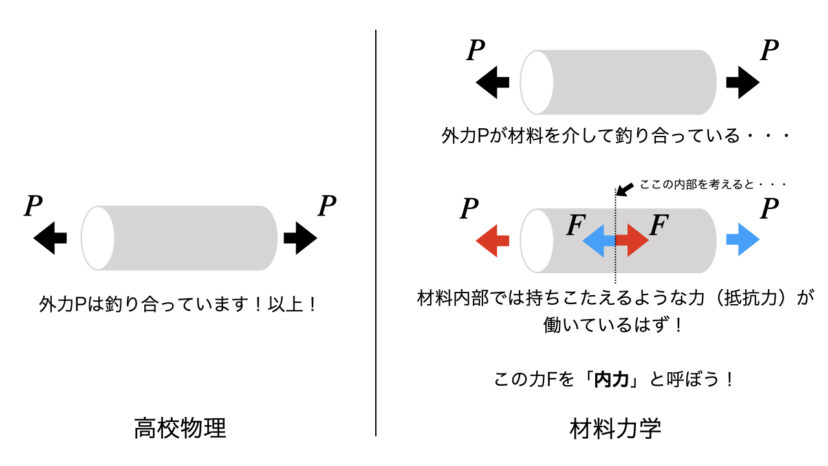
このような抵抗力のことを「内力」と言います。
そのため、内力の説明をもう少し正確に言うならば「材料の内部に発生する、外力に対する抵抗力」となります。
では次に「応力のように、なぜわざわざ単位面積あたりで評価する必要があるのか」についてですが、その理由は、材料の太さに依存しないようにするためです。
例えば「材料に100Nの内力が発生している」とだけ言われても、その材料が壊れるか壊れないかは判断できません。
「極細ポッキーみたいな細い棒に発生する100N」であればきっと壊れるでしょうし、「パルテノン神殿の柱ぐらいの太い棒に発生する100N」であればビクともしないでしょう。
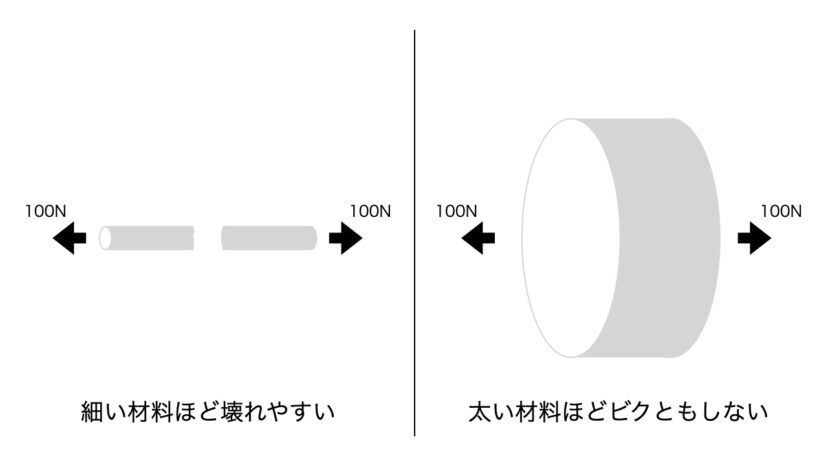
そこで、この内力を材料の断面積で割った「応力」というものを使って評価します。
応力は、力を断面積で割ったものですので、単位は[N/m2]とか[MPa]がよく使われます。
応力は材料にかかる負荷を評価するのにとても便利なものでして、100MPaで壊れることがわかっている材料は、どんなに太い材料だったとしても、基本的に100MPaの応力が加わっていれば壊れます。

外力と応力とがゴッチャにならないようにしましょう。「太い材料で100MPaの応力」ということは、加わっている外力はかなり大きいということになりますからね!例えば、断面積1mm2の棒なら外力は100Nですが、断面積100mm2の棒なら外力は10000Nです。
ひずみの定義は「材料がどの程度の割合変形したか」ということです。
$$ひずみ=\frac{材料の変形量}{材料の元の長さ}$$
また、右辺に100を掛けることで、%で表すこともできます。
$$ひずみ=\frac{材料の変形量}{材料の元の長さ}\times100 \%$$
ここでちょっと混乱しがちなのですが、ひずみの定義式の右辺の分子は「材料の変形量」であるということです。

例えば、ひずみが0%というのは「材料が全く変形しない状態」、ひずみが100%というのは「材料が2倍の長さに変形した」ということになります。たまに「材料が変形しない=100%」と勘違いする人がいるので、注意しましょう。
この理由も応力と同様で、材料の元の長さに依存しないようにするためです。
例えば「材料が1mm伸びた」と言っても、その変形量が材料にとって大きいのか小さいのかは、材料の元の長さによります。
元々1mの長さの棒が1mm伸びたというだけでは変形量は小さいですし、元々1mmの長さの棒が1mm伸びたなら、長さが倍になるわけですから変形量が大きいということになります。
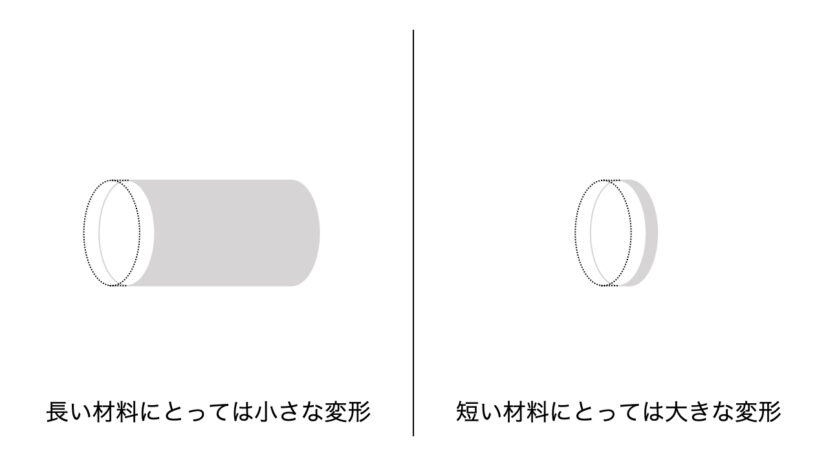
こんな状態では扱いにくいため、変形量を元の長さで割った「ひずみ」を使って評価をするのです。
「機械設計などの実務では、「応力」「ひずみ」をどのように利用しているか?」について、事例をご紹介します。
まず応力についてですが、外力がかかったことで発生した応力を、材料の耐久値と比較をして、それより大きいか小さいかを判定します。
この材料の耐久値のことを「許容応力」といいます。
もし「発生した応力 < 許容応力」ならば問題ないとなりますし、 「発生した応力 > 許容応力」ならば材料が壊れてしまう恐れがあります。
壊れてしまう恐れがある場合は、別の材料を使ったり、補強をするなどの対策をします。
ひずみについては「0.2%(=0.002)」というキーワードを覚えておいてください。
ものづくりで利用される多くの材料は、ひずみが0.2%を超えると永久変形を起こします。
実機に対しては、応力を測定するよりも、ひずみを測定するほうが簡単なので、実機が壊れそうかどうかを判定するのにひずみを測定します。
「設計では応力を」「実機ではひずみを」というイメージを持っていただければよいかと思います。

ひずみを測るのに使用する道具には「ひずみゲージ」などがあります。(Wikipediaへ)
「応力」を学習する上でよく混乱を招くのが、材料力学における「応力」と、土木・建築における「応力」の意味が異なることです。
材料力学における応力とは、「材料内部に発生する単位面積の力のこと」ですが、
土木・建築における応力は、「材料内部に発生する力のこと」、つまり「材料力学でいう内力」のことを指しています。
| 材料力学・機械工学 | 土木・建築 | |
| 内力 | 材料の内部に発生する 力 |
– |
| 応力 | 材料内部に発生する 単位面積あたりの力 |
材料の内部に発生する 力 |
| 応力度 | – | 材料内部に発生する 単位面積あたりの力 |
そのため、さまざまな参考書や技術書を読んだ時に、なんとなく言葉の違和感を感じた際は、このことを覚えておいてください。

「なんでこんな紛らわしいことするんかなぁ・・・」とたまにイラっとします笑。
なお、このブログでは、材料力学的な定義を採用しますので、ご注意ください。
今回の内容についてまとめると以下の通りとなります。
今回は以上となります。ご一読、ありがとうございました。
続きはこちら▼
材料力学を1からちゃんと学びたい人向け▼
高校の数学とか物理とかめちゃくちゃ苦手なレベルな人向け書籍▼
高校の数学・物理はある程度できる人向け書籍▼
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


材料力学における荷重の種類【全部で5つあります】
材料に発生する応力の種類【本質的には2種類しかありません】