測定とか、ノギス・マイクロメーターのことについて調べていると「アッべの原理」っていうのが出てくるけど、どういうことを言っているのかを詳しく教えて欲しい。
このような疑問・悩みを持った人へ、お答えしていきます。
ものづくりの中の検査工程では、製作する部品によって様々な検査がされますが、どのような部品でもほぼ行われるのが「寸法検査」です。

寸法検査は、部品の各寸法が図面で指示されたとおりになっているかを検査する検査です。例えば幅が10mmと図面に記載されていた場合、実際にできた部品が10mmになっているかを、測定器具を用いて測定します。実際には10mmぴったりにすることはできませんので、10mmに対して何ミリのズレを許容するかという寸法許容公差(例えば10±0.2mmなど)を定め、その範囲内に収まっているかを判断します。
ところで、検査においてとても大事なのは「検査をする以前に、そもそも検査に用いる検査器具は信頼できるのか」ということです。
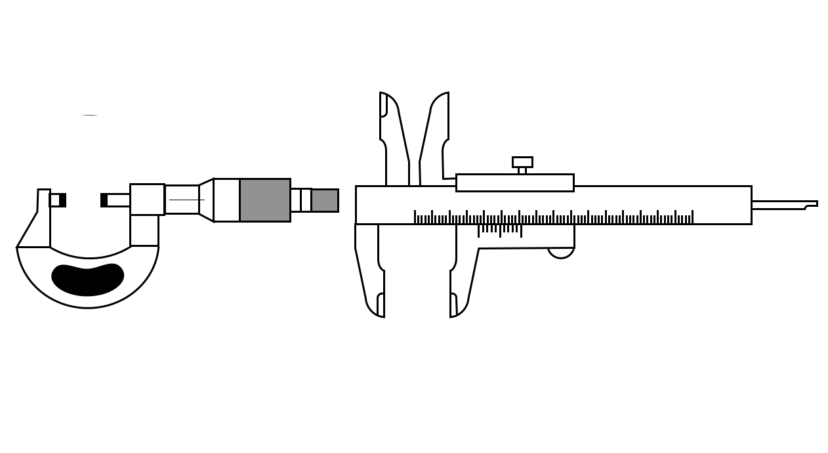
例えば、長さを測定できる器具には、「ノギス」「メジャー」「コンベックス」「鋼尺」「マイクロメーター」等がありますが、
これらの測定器具は、そもそもの測定原理からして精度の良いものと、悪いものとがあります。
精度の悪いものというのは、例えば直径が10mmであることがわかっている丸棒の径を、測定器具で測ってみると10.3mmという結果が出るというものです。
それについてまとめられたものが「アッべの原理」と呼ばれる測定精度に関する原理です。
アッべの原理を知っておくことで、
ようになります。
そこで今回は、アッべの原理と誤差について詳しくお話ししていきます。
アッべの原理とは、寸法を測定する器具の精度に関する原理で、「測定対象物と目盛りとを、同一軸上に配置することで、測定誤差を最小限にすることができる」というものです。
原理自体は、たったこれだけなのですが、少しわかりにくいかと思いますので、具体例を使って解説をしていきます。
測定器具の中でもマイクロメーターは、アッべの原理の理にかなっている測定器具ですので、非常に高い精度で寸法を測定することができます。

マイクロメーターとは、ものの寸法を0.01mm単位(場合によっては0.001mm単位)で測定できる測定器具です。最も一般的なのは、外側マイクロメーターと呼ばれる器具で、物体を挟むことによって、太さや厚さを測るために用いられます。
外側マイクロメーターの、「測定対象物」と「目盛り」との位置関係を見てみましょう。
下の図で、青い丸が測定対象物で、その青い丸の両側を挟むことで、マイクロメーターは寸法を測定します。
そして、挟んでいるもの(アンビルとスピンドル)と、挟まれているもの(測定対象物)との延長上に、目盛りが配置されています。
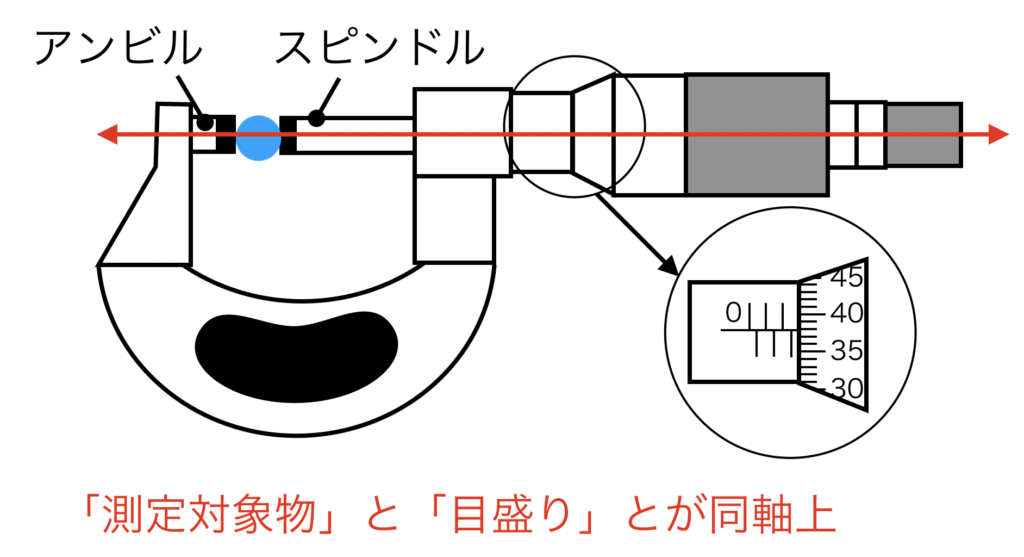
よって、マイクロメーターはアッべの原理に従った測定器具であるため、原理上は測定精度が良い(高い)と言うことができます。
一方で、よく使われる測定器具であるノギスは、アッべの理にはかなっていません。

ノギスとは、物体の「外側測定」「内側測定」「深さ測定」「段差測定」をたった1つでできる測定器具です。一般的には副尺(バーニア)と呼ばれる補助的な目盛りを併用することで、0.05mm単位で測定することができます。
ノギスの外側測定における、測定対象物と目盛りとの位置関係をみてみましょう。
ノギスは、スライダーを左右に動かすことで、ジョウを移動させることができ、このジョウで測定対象物を挟むことで測定することができます。
しかし、この挟んでいるもの(ジョウ)と、挟まれているもの(測定対象物)との延長上には、目盛りが配置されていません。
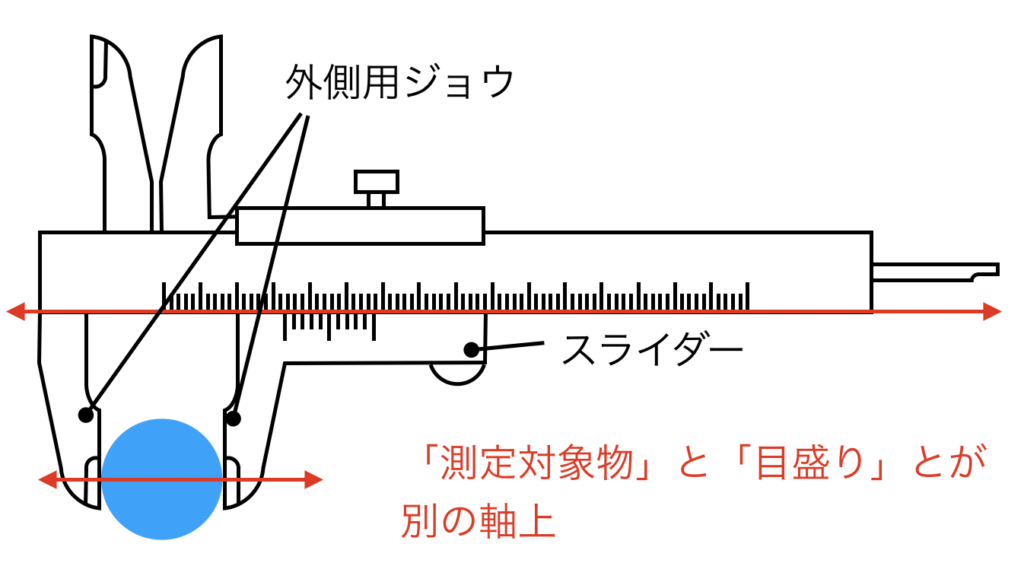
よって、ノギスはアッべの原理に従っていない測定器具であるため、原理上は測定精度が悪い(低い)のです。
なぜ、測定対象物と目盛りとが同一軸上にあると精度が高いのか?
それは、測定器具の測定子(測定対象物に当てる部分)にガタつきがあった際に発生する誤差を考えればわかりやすいです。
ガタつきがあると、測定子の部分が角度で触れることで測定誤差が生じますが、測定対象物と目盛りとが同一軸上にあると、その誤差の影響を受けにくいのです。
なお、ここでいうガタつきの規模は、0.1°程度のほんのわずかなガタつきです(パッと見でわかるほどガタついていた場合、そもそも測定器具としてNGです)。
スピンドルの支持部に角度θだけガタつくマイクロメーターを用意します。
すると、測定軸上に乗っているスピンドルの出代はLですが、角度θだけガタついていることによって、実際にはLcosθしか出ていないことになります。

よって、誤差をεとすると、以下の式が成り立ちます。
$$\varepsilon=L-L\cos\theta=L(1-\cos\theta)\cdots(1)$$
ここで、テイラー展開より(θが微小なので、高次の項は省略)、
$$\cos\theta=1-\frac{\theta^2}{2}\cdots(2)$$
となりますので、(2)式を(1)式へ代入すると、
$$\begin{align}\varepsilon&=L(1-(1-\frac{\theta^2}{2}))\\
&=L\frac{\theta^2}{2}\cdots(3)\end{align}$$
となります。ただしθは微小なので、誤差εは無視できるほど非常に小さな値となります。
そのため、測定対象物と目盛りとが同軸上にあると、測定精度が高くなるのです。
一方で、ノギスのスライダーに角度θのガタつきがあった場合について考えてみます。
ノギスの測定軸上にあらわれる測定誤差は、目盛り軸から測定軸までの距離に依存します。
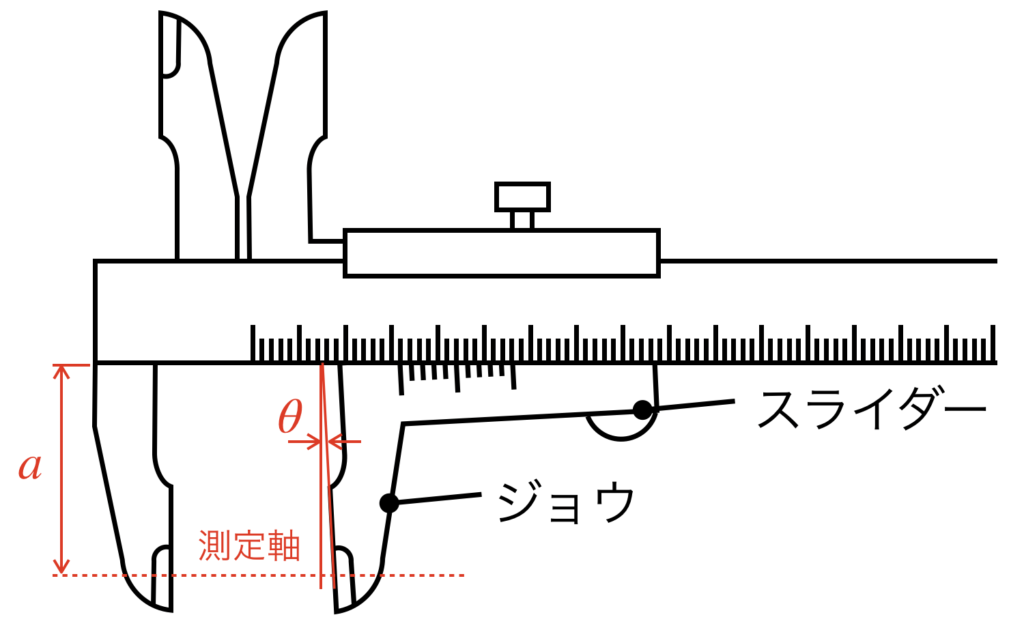
よって、誤差をεとすると、以下の式が成り立ちます。
$$\varepsilon=a\tan\theta\cdots(4)$$
ここで、θが微小であることに注目すると、以下の近似式が成立します。
$$\tan\theta\simeq\theta\cdots(5)$$
よって、(5)式を(4)式へ代入すると、
$$\varepsilon=a\theta\cdots(6)$$
となり、θが微小とはいえ、マイクロメーターと比較すると誤差が大きくなってしまうことがわかります。
そのため、測定対象物と目盛りとが同軸上にないと、測定精度が低くなるのです。
なお、この誤差は、スライダー部のガタつきの他にも、ジョウを測定対象物に当てたときの「たわみ」によっても発生します。
今回のポイントをまとめると以下のとおりとなります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

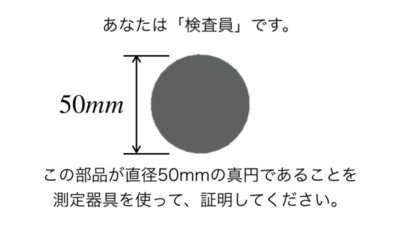
真円度の測定・証明方法【検査】
マイクロメーターの使い方と読み方【割とデリケートな測定器具です】