【要注意】トルク法でボルトを締める際の、軸力のばらつきの大きさ

この記事をシェアする
Twitter
LINE
はてブ
Facebook

この記事を読むべき人

設計でボルトを選定することが多いという人
上司たちが「軸力はばらつく」と言っていたけれど、それがなんでなのかを知りたいという人
ねじを締めるのって簡単そうにしか思えないんだけれど、何か知っておくべきことがあるのか気になる人

こんにちは、リヴィです。

「機械の設計」と一言でいっても、「どんな機械を設計するのか？」によって求められる能力・スキルは異なってきます。

ところが、どんな機械を設計するにしても、ほぼ間違いなく関わることになるのが「ねじ」です。

私は比較的小さな機械の設計もすることも多いのですが、机の上に乗るようなサイズでも、使うねじの本数が100本を超えることも珍しくありません。

このねじを締める方法には、実はいくつか種類があるのですが、最も多用されるのが「トルク法」という締め方です。

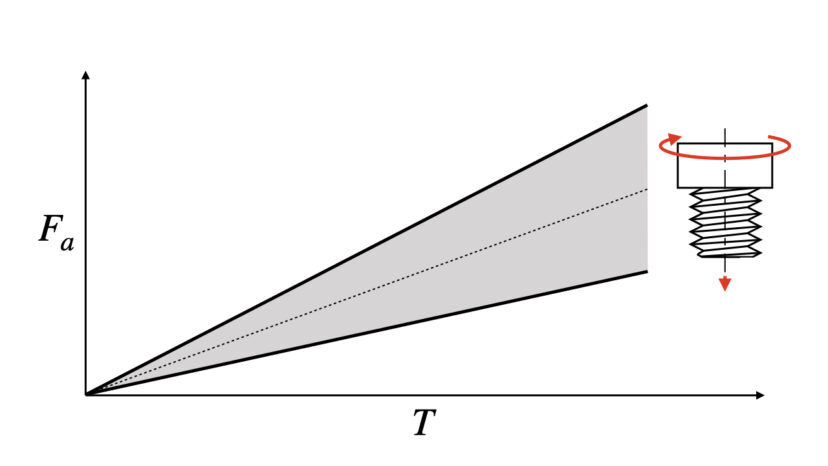
トルク法とは「以下の軸力とトルクの関係式を使って、ねじを締めたときの軸力から逆算してトルクを求め、そのトルクでねじを締める」という軸力の管理方法です（詳しくはこちらの記事で解説しています）。

$$T=F_a \left (\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+\mu_w \frac{d_w}{2} \right)$$

$$T$$	締付けトルク[N･m]
$$F_a$$	軸力[N]
$$P$$	ねじのピッチ[mm]
$$d_2$$	ねじの有効径[mm]
$$μ_s$$	ねじ面の滑り摩擦係数[-]
$$\alpha$$	ねじ山の半角[°]
$$\mu_w$$	座面の滑り摩擦係数[-]
$$d_w$$	等価摩擦直径[mm]

$$(簡易版)\hspace{18pt}T=KF_ad\hspace{18pt}$$

$$T$$	締付けトルク[N･m]
$$K$$	トルク係数[-]
$$F_a$$	軸力[N]
$$d$$	ねじの呼び径[mm]

トルク法には、

トルクレンチを使うだけでよいので、施工が簡便であること
ボルトが弾性変形する範囲内で締め付けるため、取付け・取外しの頻度が多い部分に適している

といったメリットがあることから、非常に多くの場面で使われます。

ボルトを100本も締めないといけないというときに、いちいち手間を掛けていられないですもんね！

ところが、トルク法には致命的にもなりうるデメリットがあります。

それは「軸力のばらつきが大きい」ということです。

要するに、上記の締付けトルクとボルトの関係式を使って締付けトルクを計算し、そのトルクになるように締付けたとしても、「実際の軸力」が「計算した軸力」と大きく乖離しやすいのです。

具体的な例を挙げると、母材もボルトも同じ材料・同じ寸法で、かつ同じトルクをかけて締め付けたとしても、実際の軸力が小さ過ぎたり、大き過ぎたりするということです。

そのため、特に理論とか計算とかが得意な設計者にとっては、大きな落とし穴だったりします。

よくある設計者の考えとしては、

「いやいや、軸力が低くなっちゃうと、強度的にアウトになっちゃうから！なんなら手間をかけてでも、測定するなりして、品質を保証してよ！」

ですが、現場側は、

現場側は「いやいや、そもそも強度に余裕を持たせて設計してもらわないと困るし！ってか、何百・何千とあるボルトを1個1個測定していたら納期間に合わないし！」

となります。

そうやって、設計者側と現場側との間でよく揉めごとになったりもします（笑）。

そこで今回は「トルク法でボルトを締める際に注意しておくべき、軸力のばらつきの大きさ」についてお話ししていきます。

この記事を読んで、ボルトに関する設計をする際に「理論的にどうなのか」と「実際はどうなのか」という2つの視点から考えられるようにしていきましょう。

1 ばらつきの主な原因は「摩擦係数」
2 締付け係数を見てみよう
3 軸力のばらつきの対策
4 まとめ

ばらつきの主な原因は「摩擦係数」

軸力が計算通りになりにくい主な原因は「摩擦係数の定量化が困難であること」です。

以下に、締め付けトルクと軸力との関係式を再掲しますが、この中の「ねじ面の滑り摩擦係数μ_s」と「座面の滑り摩擦係数μ_w」の数値に大きなばらつきがあるのです。

$$T=F_a \left (\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+{\mu_w} \frac{d_w}{2} \right)$$

これらの摩擦係数の値は、一意的にバシッと決まるわけではなく、

ねじ締めをする材質の組み合わせ
締付け速度
接触面の粗さ
接触面のへたり具合
ねじの個体差
傷やバリの程度
汚れの付着具合
温度、湿度・・・

など、様々な要因が非常に複雑に影響することでかなり変化します。

ちなみに、こういった摩擦などを中心に取り扱う科学分野のことを「トライボロジー」といいます。かなり高度に科学技術が発展してきた現代ですら、めちゃくちゃ定量化が難しい分野の一つです。

締付け係数を見てみよう

軸力のばらつきの程度を見るために使われる値として「締付け係数」というものがあります。

締付け係数とは、ある締付けトルクでねじを締めた際に発生する軸力の、最小値と最大値との比のことを言います。

式で表すと以下のとおりです。

$$Q=\frac{F_{max}}{F_{min}}$$

$$Q$$	締付け係数[-]
$$F_{max}$$	軸力の最大値[N]
$$F_{min}$$	軸力の最小値[N]

式を見て分かる通り「Qの値が1に近いほど、ばらつきが小さい」という意味になります。

では、他の軸力の管理方法と比べ、トルク法の締付け係数はどうなのかというと、以下の表のとおりとなります。

代表的なねじ締付け管理方法^[1]
軸力の管理手法	締付け係数Q（参考値）
トルク法	1.4～3
弾性域回転角法	1.5～3
塑性域回転角法	1.2
トルク勾配法	1.2

1：JIS B 1083を参考に作成

表を見て明らかなように、トルク法の締付け係数は他の締め付け方法と比べて大きい事がわかります。

補足：締付け係数について解説

締付け係数は、わかりやすいようで若干わかりにくい指標です。

なぜなら、締付け係数は、ばらつく軸力の中の最小値と最大値を比較したものなので、目標とする軸力に対しての数値ではないからです。

ただ、締付け係数を使って、目標とする軸力に対してどれだけばらつくのかは、計算によって求めることができます。

前提として、目標とする軸力は、最小軸力と最大軸力とのちょうど間の数値であるとします。

$$F_{mid}=\frac{F_{max}+F_{min}}{2}\cdots(1-1)$$

$$F_{mid}$$	目標とする軸力[N]
$$F_{max}$$	軸力の最大値[N]
$$F_{min}$$	軸力の最小値[N]

ここから、「締付け係数がQののとき、目標軸力に対し±何%ばらつくのか」を計算していきます。

ばらつきをx%とすると、解くべき方程式は以下のとおりとなります。

$$\begin{cases}
F_{max}=(1+\displaystyle\frac{x}{100})F_{mid}\cdots(1-2)\\
F_{min}=(1-\displaystyle\frac{x}{100})F_{mid}\cdots(1-3)\\
F_{max}=Q\cdot F_{min}\cdots(1-4)
\end{cases}$$

(1-2)式、(1-3)式を(1-4)式に代入して、

$$(1+\displaystyle\frac{x}{100})F_{mid}=Q(1-\displaystyle\frac{x}{100})F_{mid}\cdots(1-5)$$

これを整理すると

$$x=\frac{Q-1}{Q+1}\cdot100$$

これが、目標とする軸力に対するばらつきを表す式となります。

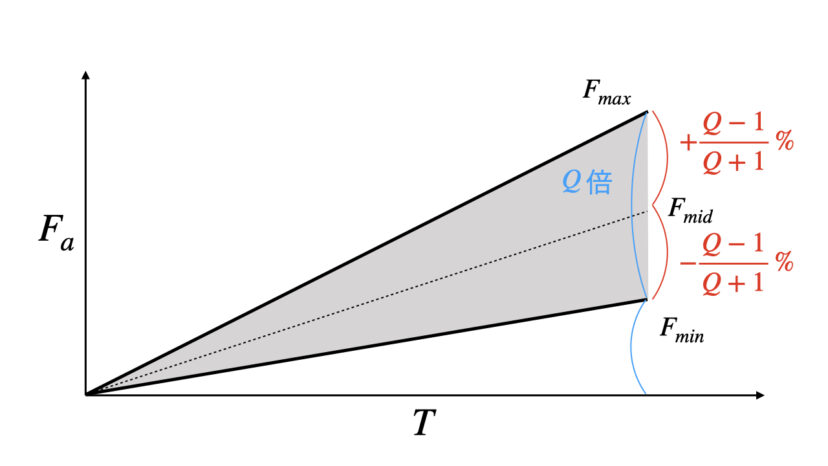
例えば、締付け係数Q=3というのは、目標とする軸力F_midに対して、実際の軸力は±50%ばらつくという意味になります。

軸力のばらつきの対策

ばらつきの大きなトルク法ですが、実はトルク法の中でも、どのような条件でボルトを締めるかによって、締付け係数Qの値は大きく変わってきます。

以下に、条件ごとの締付け係数の値を示します。

締付け係数Q^[1]
締付け係数Q	締付け方法	表面状態		潤滑状態
締付け係数Q	締付け方法	ボルト	ナット	潤滑状態
1.25	トルクレンチ	マンガンリン酸塩	無処理,リン酸塩	油潤滑,MoS₂ペースト
1.4	トルクレンチ,トルク制限付きレンチ	無処理,リン酸塩
1.6	インパクトレンチ	無処理,リン酸塩
1.6	ボルトの伸び測定	すべての場合	すべての場合	すべての場合
1.8	トルクレンチ,トルク制限付きレンチ	無処理,リン酸塩	無処理	潤滑せず
2	インパクトドライバ,動力ドライバ	無処理,リン酸塩	無処理	潤滑せず
		亜鉛,カドミウムメッキ	無処理	油潤滑,潤滑せず
		亜鉛メッキ	亜鉛メッキ
		カドミウムメッキ	カドミウムメッキ
	ナット回転角法	すべての場合	すべての場合	すべての場合
3	長柄スパナによる人力締付け	すべての場合	すべての場合	すべての場合

1：山本晃,ねじ締結の理論と計算

ここから言える、軸力のばらつきをできるだけ抑えるために重要なことは次のとおりです。

トルクレンチを使おう

軸力が重要な箇所については、トルクレンチを使うようにしましょう。

インパクトドライバや動力ドライバを使うよりも、トルクレンチを使ったときのほうが締付け係数が小さくなっていることがわかります。

トネ(TONE) プレセット形トルクレンチ差込角12.7mm(1/2″) T4HC140 140N・m

created by Rinker

トネ(TONE)

トネ(TONE) ドライバーデジトルクセット DBDT3S ビット差込ブラック 300cN・m

created by Rinker

トネ(TONE)

もっとばらつきを抑えるために

トルクレンチを使うからと言って、過信は禁物です。

締付け係数はあくまで目安の数値のため、少し雑なことをしただけで、ばらつきがそこそこ大きくなります。

トルク管理の厳しいプロジェクトになると、ボルトの締付けに関して以下の要件があったりします。

トルクレンチは新品を用いるか、○ヶ月以内に校正をしたものを用いること
トルクレンチの個体差をなくすため、同じトルクレンチを用いること
トルクレンチで締める際は、可能な限り勢いをつけずに締めること
トルクレンチの「カチッ」という音は2回確認すること。
使用するトルクレンチのメーカー名・型式・シリアルNo.を記録すること
トルク締めをした日時と作業者を記録すること

これらは、社内基準として定められていることもありますし、お客さん側の基準として定められていることもあります。

潤滑剤を使う

もう一つの対策は潤滑剤を使うことです。

潤滑剤にはいろいろと種類がありますが、よく使われるのが二硫化モリブデン(MoS₂)です。

モリブデングリース

created by Rinker

KURE(呉工業)

潤滑剤を使ったら、ねじが緩みやすくなるんじゃないの？

潤滑剤を使うことで、計算上の軸力と、実際の軸力との値を近づけることができます。

ですが、「ヌルヌルしたものを塗ってしまったら、ねじが緩みやすくなるんじゃないの？」と気になる人もいるかと思います。

たしかに、私のブログでは「ねじが緩まないのは摩擦力のおかげ」とさんざん解説しているので、そう思うのも無理がないと思います。

ただ結論から言うと、摩擦係数が低下したことが原因でねじが緩むことは起こりにくいです。

以前私の記事で、ねじが緩む条件として、以下の式を解説しました（詳細はこちらの記事で解説しています。）。

$$T>F_a \left (-\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+\mu_w \frac{d_w}{2} \right)$$

$$T$$	トルク[N･m]
$$F_a$$	軸力[N]
$$P$$	ねじのピッチ[mm]
$$d_2$$	ねじの有効径[mm]
$$μ_s$$	ねじ面の滑り摩擦係数[-]
$$\alpha$$	ねじ山の半角[°]
$$\mu_w$$	座面の滑り摩擦係数[-]
$$d_w$$	等価摩擦直径[mm]

ただし、この式のみが考慮されるのは「工具を使ってねじを取り外そうとした場合です。

「ねじが緩む条件」というよりは、「ねじを外す条件」という方が正確かもしれません。

一方で、実際において緩みが問題となるのは「機械の振動などによって、ねじが徐々に緩んでくる現象」であり、その話は上記の式で完結できるほど単純ではないです。

詳しい話は以下の論文で示されておりますが、少なくとも潤滑によりヌルヌル滑って緩んでくるという現象は起こりにくいと結論付けられております。

酒井智次, ボルト軸方向の繰返し引張荷重作用下のねじの回転ゆるみ機構,日本機械学会論文集(A編)78巻786号(2012)

やはり軸力のばらつきが大きいことが、ねじの緩みに与える影響が大きいようです。目標軸力に対して高すぎて母材が陥没したり、低すぎて緩んだりといった感じですね。

潤滑ありの場合の注意点

潤滑ありでボルトを締結しようとする際には一つ注意点があります。

それは、潤滑なしに比べて潤滑ありのほうが締付けトルクは低くなることです。

実際に計算をして、「同じ締付けトルクで締めた場合」の潤滑なしとありとを比較していきます。

ある締付けトルクでボルトを締めたときに発生する軸力は、以下の式のとおりとなります。

$$F_a=T \left (\frac{2\pi}{P}+\frac{2\cos\alpha}{d_2\mu_s}+\frac{2}{1.3 d\mu_w} \right)$$

$$T$$	締付けトルク[N･m]
$$F_a$$	軸力[N]
$$P$$	ねじのピッチ[mm]
$$d_2$$	ねじの有効径[mm]
$$μ_s$$	ねじ面の滑り摩擦係数[-]
$$\alpha$$	ねじ山の半角[°]
$$\mu_w$$	座面の滑り摩擦係数[-]
$$d_w$$	等価摩擦直径[mm]

ここで、以下の条件で計算をしていきます。

ねじはM6とする
締付けトルクを10N･mとする（実際の締付けトルクではなく、あくまで試算をするだけの参考値です）
ねじ面・座面の摩擦係数は等しいとする
摩擦係数は、潤滑なしは0.15、潤滑ありは0.05とする
等価摩擦直径は1.3D（Dはねじの呼び）とする

その計算結果は以下のとおりです。

潤滑なしの軸力	潤滑ありの軸力
100 N	173 N

このとおり、潤滑ありのほうが1.7倍ぐらい大きな軸力となってしまいます。

その理由は、締付けトルクをかけたときに、その力が「ねじの摩擦に打ち勝つための力」に使われるか、「軸力の発生に使われるか」の割合が変化したためです。

潤滑無しでトルクを掛けると、かけた力のうちたった10%程度しか軸力発生に寄与しない（残りは摩擦力に打ち勝つための力に使われる）のですが、潤滑ありだと軸力発生への寄与は24%程度まで上昇します。

つまり、潤滑をしたボルトを、潤滑なしと同じ締付けトルクで締めた場合、ボルトが塑性変形する可能性が高いということになります。

そのため潤滑ありでは、潤滑なしよりも低い締付けトルクで締めつけて、適正軸力にする必要があります。

ほとんどの人は「締付けトルクはちょこちょこっとググって、最初に出てきたページの締付けトルクの値を参照している」と思いますが、

その締付けトルクは、どんな締付け方法のトルクなのか、確認しているでしょうか？

そこの前提条件を見落とすと、オーバートルクとなり、ボルトがくびれたりする可能性が高くなります。

締付けトルクを調べるサイトによって値がバラバラな理由として、潤滑条件の違いだけではなく、そもそも摩擦係数自体が一意に決まる値ではないこととが混在しているためです。ただ、締付け係数を見れば、ある程度は締付けの条件を想定することができます。

以下に、摩擦係数・トルク係数ごとの、ねじ面摩擦力、座面摩擦力、軸力発生への寄与の割合を示します。

摩擦係数とトルク係数（並目ねじ）^[1]
μ	K	ねじ面摩擦力	座面摩擦力	発生軸力
0.05	0.079	35.1%	41.0%	24.0%
0.075	0.109	38.1%	44.5%	17.4%
0.1	0.140	39.8%	46.6%	13.6%
0.125	0.170	40.9%	47.9%	11.2%
0.15	0.200	41.7%	48.8%	9.5%
0.175	0.230	42.3%	49.4%	8.3%
0.2	0.260	42.7%	50.0%	7.3%
0.25	0.321	43.4%	50.7%	5.9%
0.3	0.381	43.8%	51.2%	5.0%
0.35	0.441	44.1%	51.6%	4.3%
0.4	0.501	44.4%	51.9%	3.8%

摩擦係数とトルク係数（細目ねじ）^[1]
μ	K	ねじ面摩擦力	座面摩擦力	発生軸力
0.05	0.072	39.4%	45.3%	15.3%
0.075	0.102	41.5%	47.7%	10.8%
0.1	0.133	42.6%	49.1%	8.3%
0.125	0.163	43.4%	49.9%	6.8%
0.15	0.193	43.9%	50.5%	5.7%
0.175	0.224	44.2%	50.9%	4.9%
0.2	0.254	44.5%	51.2%	4.3%
0.25	0.315	44.9%	51.6%	3.5%
0.3	0.376	45.1%	51.9%	2.9%
0.35	0.436	45.3%	52.1%	2.5%
0.4	0.497	45.5%	52.3%	2.2%