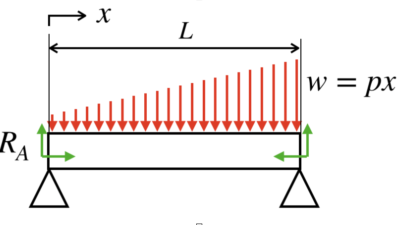
今回は、梁に曲げ荷重が作用している時の「内力」についてお話しします。
引張荷重・圧縮荷重・せん断荷重の話と同様に、材料に曲げ荷重が作用した際にも、材料の内部には「内力」が発生します。
曲げ荷重になっても、考えるべきことは今までと一緒です。
それは、以下の3ステップです。
ただ、今までの引張荷重や圧縮荷重、せん断荷重の問題と違うところは、
内力をグラフ化することが多いという点です。
なぜなら、1本の梁の中でも、場所によって内力が異なることが多いためです。
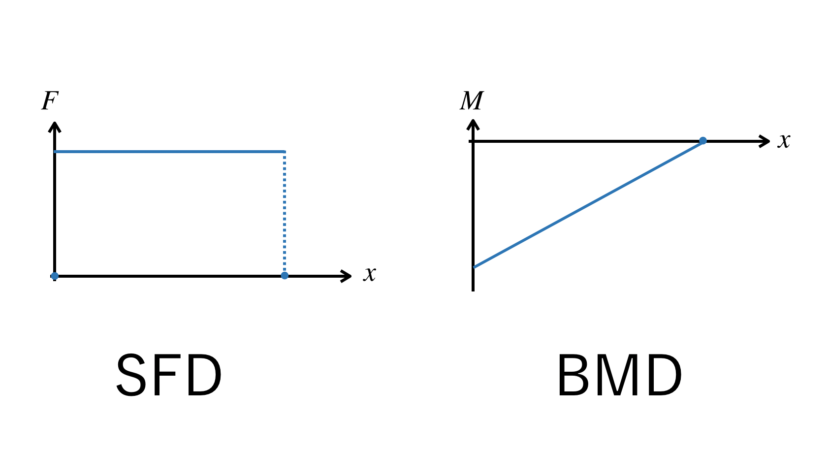
そのグラフは、SFDやBMDと呼ばれています。
今回は、梁の問題について、SFDやBMDを作図するところまでをお話しします。
曲げ荷重における釣り合いの式は次の3つを考える必要があります。
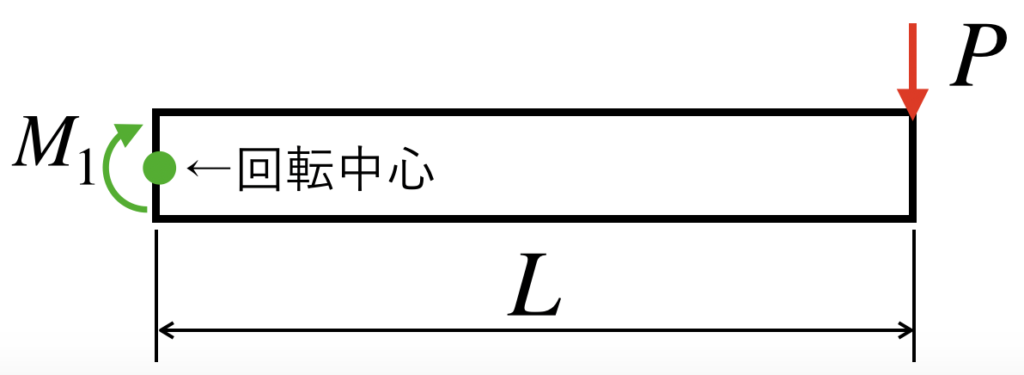
ここでは、下図の片持ち梁を例にあげながら話をしていきます。
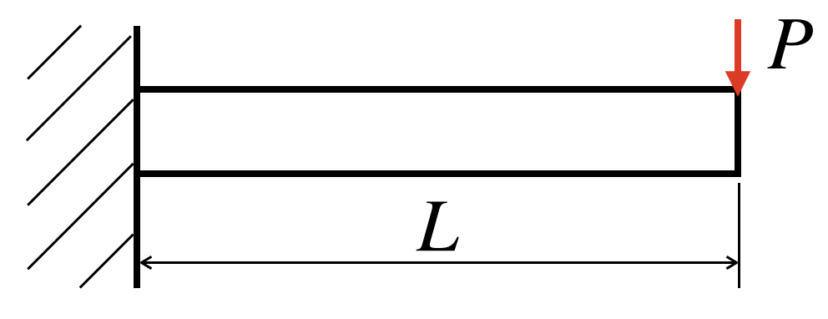
梁が片側固定端で支持されています。
まずは、梁が固定端から受ける反力について確認していきます。
固定端は、「上下」「左右」「回転」について拘束する支持方法ですので、
梁が受ける反力は、
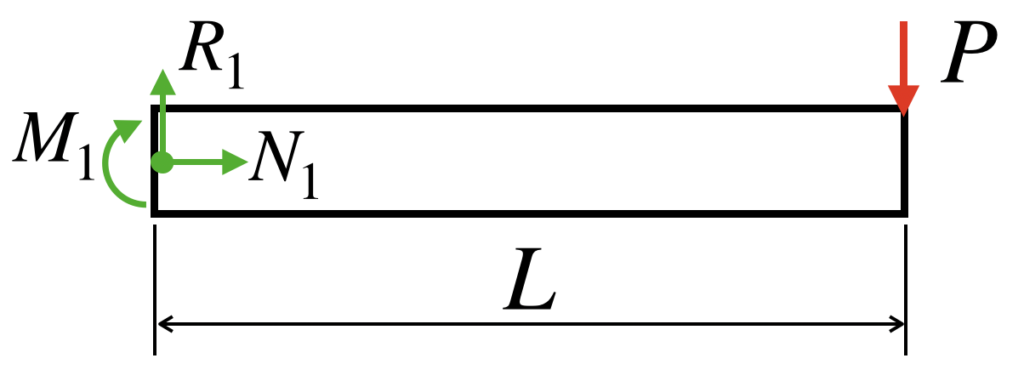
R1:上下方向の反力
N1:左右方向の反力
M1:回転方向の反力
となります。
まずは上下、左右方向について、釣り合いの式を立てると、以下のとおりとなります。
[mathjax]
$$\begin{align}
&(上下方向):R_1-P=0\cdots(1)\\
&(左右方向):N_1=0\cdots(2)\\
\end{align}$$
回転方向の釣り合いの式を立てる時は、梁が支持されている箇所を中心に、
「右回転の力を正、左回転の力を負」としています。
釣り合いの式は以下のとおりです。
$$\begin{align}
(回転方向):M_1+PL=0\cdots(3)
\end{align}$$
ここまでできたら、
「仮想的に切り離し、内力を求める」
という流れになるのですが、
曲げ荷重の問題では、これをグラフ化することが多いです。
ここで出てくるグラフは、
SFD(せん断力図)
BMD(曲げモーメント図)
と言われています。
グラフというと、身構えてしまいがちですが、
要するにやりたいことは、
「仮想的に切り離して、内力を求める」
ことです。
梁の長手方向をx軸として、梁の内部に発生する上下方向の力(せん断力)をグラフ化したものです。
SFDはSharing Force Diagramの略です。
「SFD」という用語を丸暗記するよりは、何の略なのかを知っておいた方が覚えやすいです。
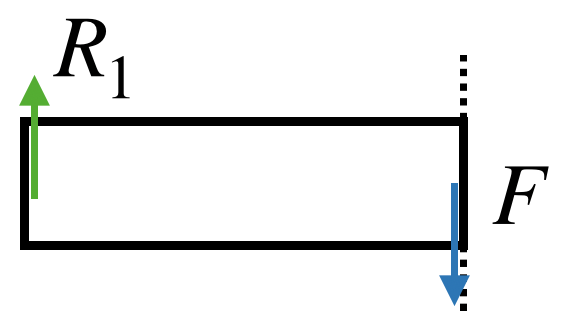
では、グラフを書く前に、まずは梁を仮想的に切り離してみましょう。
$$\begin{align}
R_1-F&=0\cdots(4)
\end{align}$$
(1)式と(4)式より、
$$
\begin{align}
\begin{cases}
R_1-P&=0\cdots(1)\\
R_1-F&=0\cdots(4)
\end{cases}\\
\end{align}
$$
$$F=P\cdots(5)$$
適当なところで仮想的に切り離して、内力を求めましたが、
今回の場合は、梁のどこで仮想的に切り離しても、内力は変わりません。
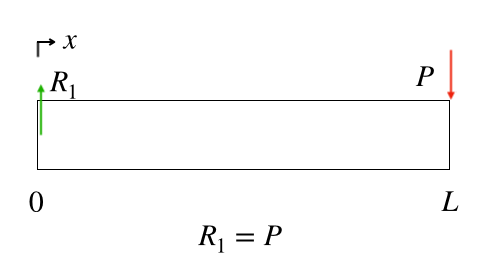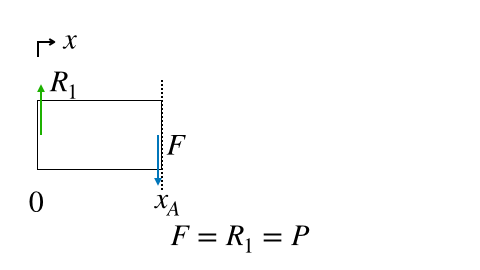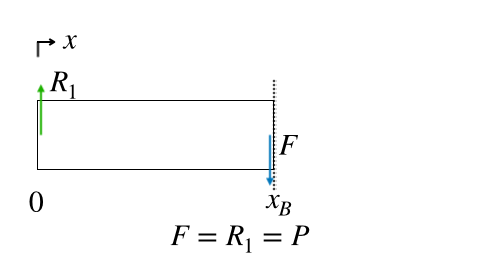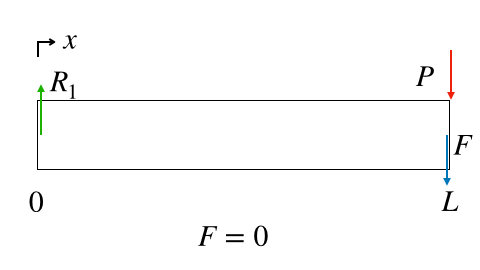
つまり、SFDで表すと、以下のグラフになります。

梁の長手方向をx軸として、梁の内部に発生する回転力(モーメント荷重)をグラフ化したものです。
BMDはBending Moment Diagramの略です。
では、仮想的に切り離して考えてみましょう。
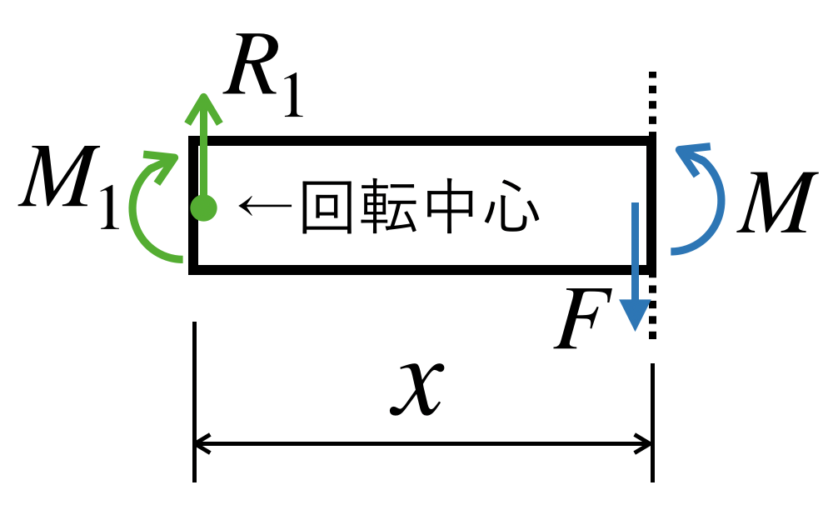
ここで重要なのは、仮想断面にも「曲げモーメント」が内力として発生しているということです。
この仮想断面に発生している内力が、BMDの縦軸になります。
さらに、モーメントを考える上では「力が発生している位置」も重要な要素になります。
ここでは、仮想的に切り離した位置をxとし、梁の左端を回転中心として式を立ててみます。
$$\begin{align}
M_1+R_1\cdot0+F\cdot x-M =0\cdots(6)
\end{align}$$
(3)式、(5)式、(6)式より、
$$
\begin{align}
\begin{cases}
M_1+PL=0\cdots(3)\\
F=P\cdots(5)\\
M_1+R_1\cdot0+F\cdot x-M=0\cdots(6)
\end{cases}\\
\end{align}
$$
$$M=Px-PL$$
この式をみますと、x=0のとき(梁の左端)で、大きさがPLで、向きが左回転のモーメントが発生しています(マイナスは「向きが反対」という意味です)。
そして、x増える(梁の右側へ移動する)につれて、モーメントの大きさが小さくなっていき、
x=L(右端になったところ)で、モーメントが0になります。(|M|はMの絶対値という意味です)

これをBMDで表すと、グラフは以下のようになります。
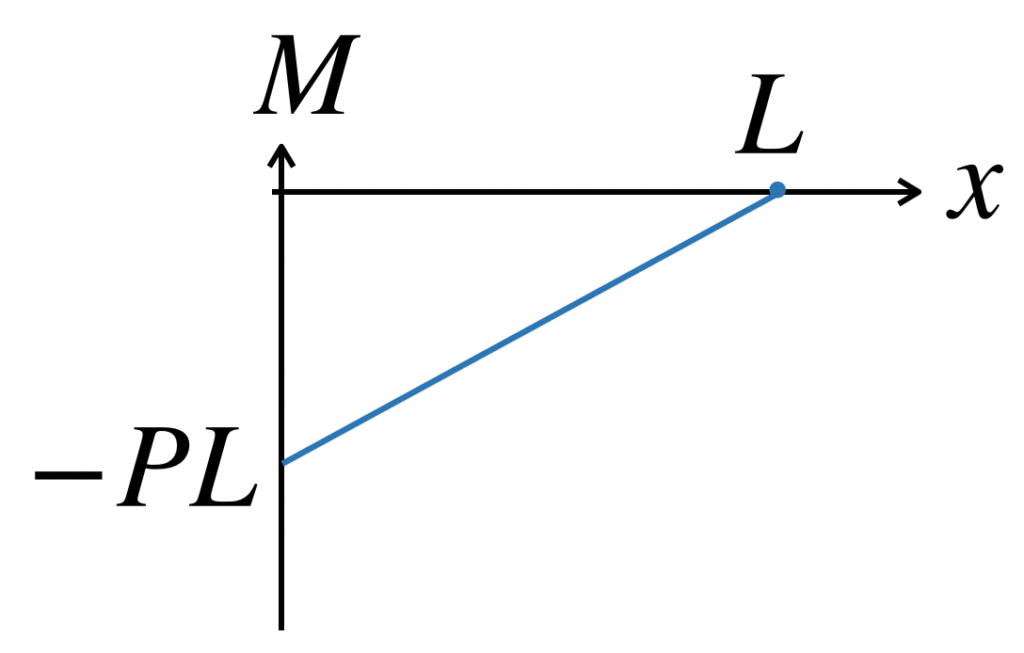
SFDは上下方向の内力、BMDは回転方向のモーメントでしたが、左右方向についてはありません。
確かに左右方向についてグラフを書こうと思えば書けますが、
材料力学で出てくる問題のほとんどは、(2)式にあるように、
水平方向の反力は0として計算されます。
そのため、左右方向に関するグラフを書いたところで、面白みのないグラフができてしまうのです。
また、左右方向に関する力は、回転方向の釣り合いの式とは関係がありません(回転力として作用しません)。
そのため、通常は書かないことが多いです。
もし、水平方向の外力が作用している際は、引張・圧縮の演習問題のように解けばOKとなります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


断面二次モーメントってどんな意味か? についての解説
分布荷重の場合のSFD BMDの書き方