今回は演習問題です。
問題は全部で3問あります。
下の方に解答を載せておりますので、答え合わせにご使用ください。
なお、この演習問題では、以下の内容が前提となっております。
直径40mmの丸棒Aの片側が壁に固定されており、丸棒Aのもう片側が直径80mmの丸棒Bの片側と固定されています。丸棒Bのもう片側を人が100 Nで引張ります。棒は釣り合いの関係にあるとき、次の問いに答えてください。
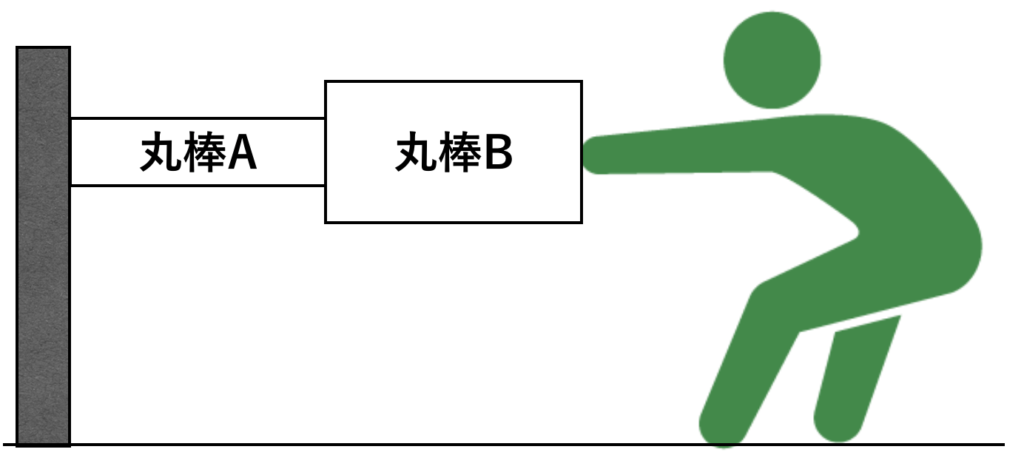
(1) 棒が壁から受ける反力の大きさを求めてください。
(2) 丸棒A・丸棒Bに働く応力をそれぞれ求めてください。ただし、引張応力をプラス、圧縮応力をマイナスの符号で表すとします。
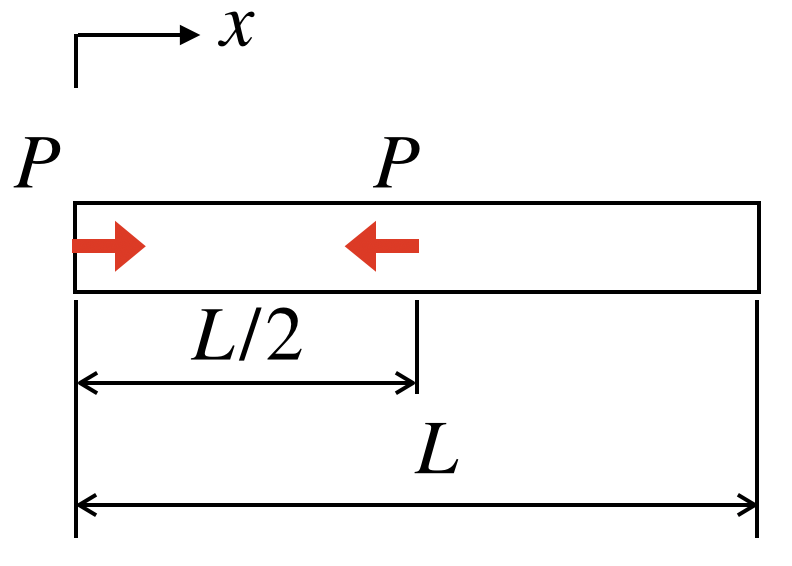
長さL、直径dの丸棒に対して、下の図の位置に大きさPの圧縮荷重がかかっているとします。棒の左端をx軸の原点としたとき、横軸を棒の長さ、縦軸を棒に発生する応力としたグラフとして表してください。
ここで、L=1000 mm、d=20 mm、P=100 Nとし、棒は釣り合いの関係にあるとします。
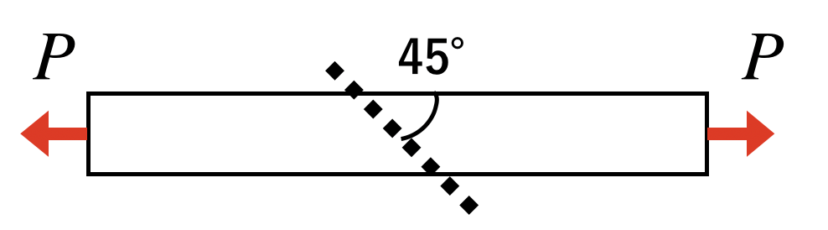
壁に固定された、直径dの丸棒の両端を力Pで引張ります。
下の図のように、棒の長手方向に対して45°で仮想的に切り離したときの、垂直応力、剪断応力をそれぞれ求めてください。
ここで、d=50 mm、P = 200 Nとし、また、楕円の面積は、長軸の長さを2a、短軸の長さを2bとすると、πabで求められるものとします。
(1)棒は人間から100Nの引張荷重を受けていることから、棒は壁に対して100Nの力を与えています。釣り合いの関係にあることから、棒が壁から受ける反力は100Nです。
(2)以下の①、②の位置で仮想的に切り離して、それぞれの場合について1つずつ考えていきます。
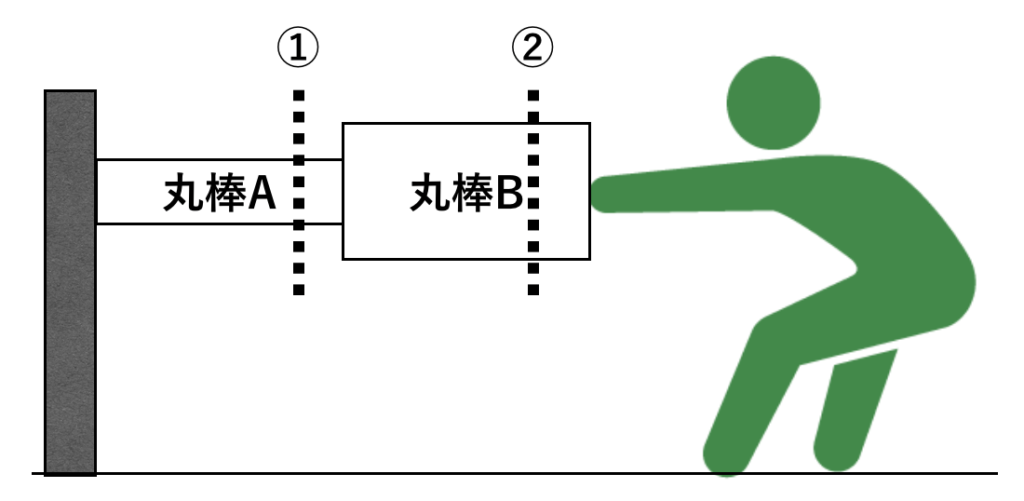
仮想的に切り離した左側について考えると、①の仮想断面には外力と釣り合う内力が発生していると考えることができます。
よって、力の関係は以下の通りとなります。

応力の定義より、
$$\sigma=\frac{F}{A}$$
| $$\sigma$$ | 応力[N/mm2] |
| $$F$$ | 内力[N] |
| $$A$$ | 仮想断面の面積[mm2] |
値を代入すると、
$$\sigma=\frac{100N}{(\pi\times (40mm)^2)/4}\simeq8.0\times10^{-2} N/mm^2$$
答え 丸棒A:8.0 N/mm2 丸棒B:2.0 N/mm2
仮想的に切り離した左側について考えると、①と同様、②の仮想断面には外力と釣り合う内力が発生していると考えることができます。

応力の定義に値を代入すると、
$$\sigma=\frac{100N}{(\pi\times (80mm)^2)/4}\simeq2.0\times10^{-2} N/mm^2$$
仮想断面の位置が(0<x<L/2)、(L/2≦x<L)の2つの場合に分けて考えます。
仮想的に切り離し、力の関係について整理します。
内力をFとすると下の図のようになります。
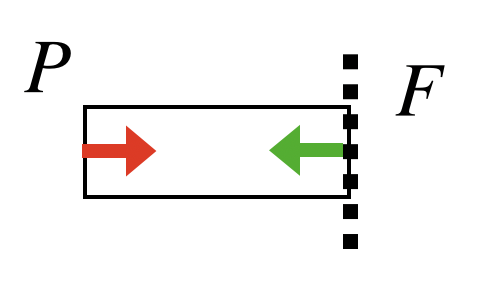
すると、以下の式が成り立ちます。
$$P-F=0\\F=P$$
よって応力は以下の通りになります。(圧縮応力の符号をマイナスとする点に注意してください)
$$\sigma=-\frac{F}{\pi d^2/4}=-\frac{P}{\pi d^2/4}=-\frac{100N}{\pi (20mm)^2/4}\simeq-0.3 N/mm^2$$
仮想的に切り離し、力の関係について整理します。
内力をFとすると下の図のようになります。
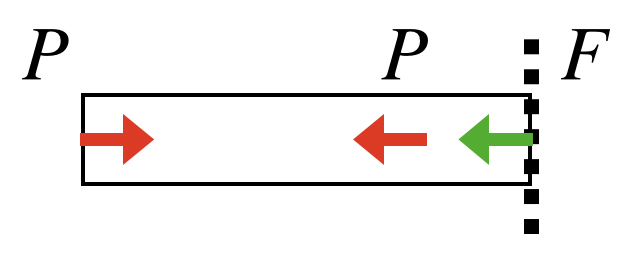
$$P-P-F=0\\F=0$$
内力が0 Nなので、
$$\sigma=0 N/mm^2$$
(a)、(b)より、グラフに表すと、以下の通りになります。
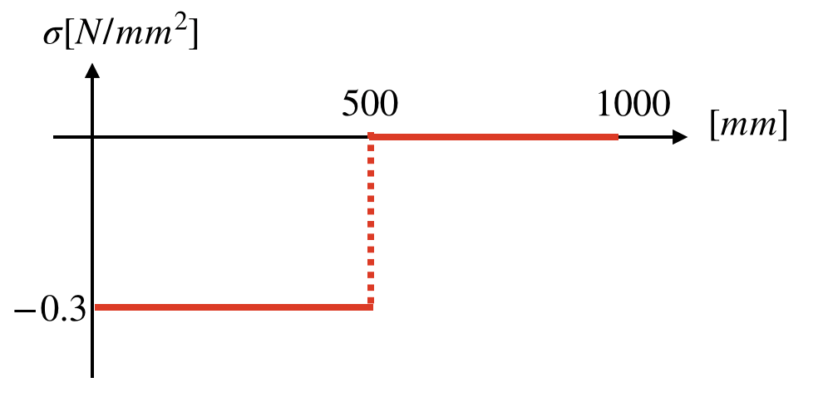
問題の図にあった通り、棒を仮想的に切り離しますと、以下のとおりになります。
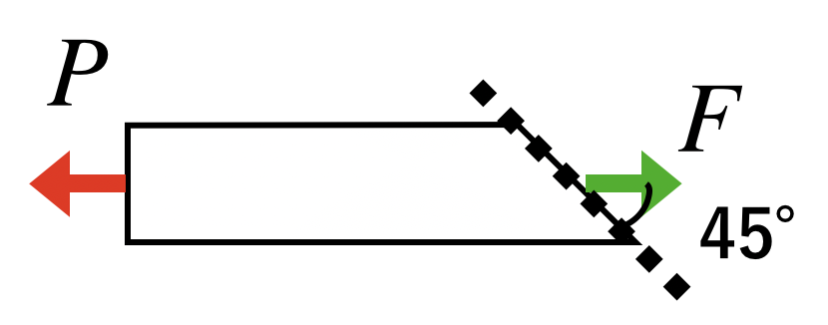
$$F=P$$
これでは、仮想断面に対して内力の方向が平行でも垂直でもないので、この内力を分解します。
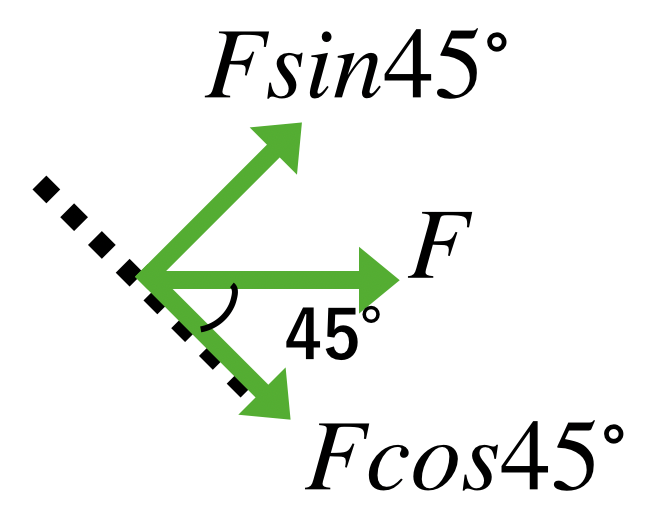
また、丸棒を斜めに切断すると、断面の形状は楕円となります。
ここで、楕円の短軸の長さは丸棒の直径と同じく50 mmです。
楕円の長軸の長さは、
$$\sqrt{2}d = \sqrt{2}\cdot 50 mm\simeq 70.7 mm$$
となります。
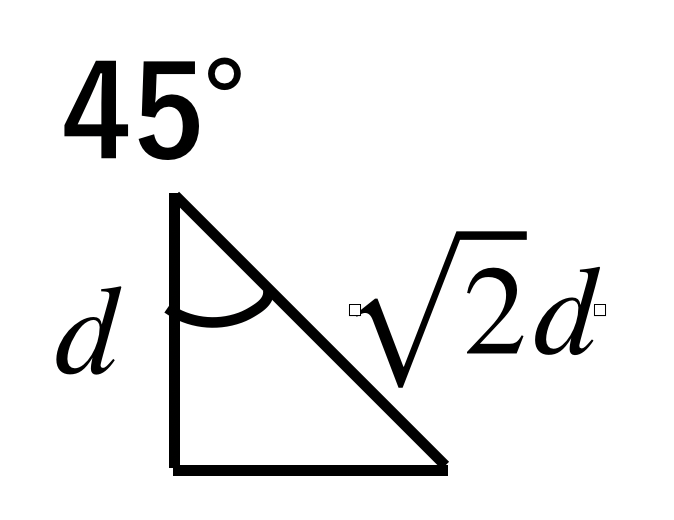
よって、
$$2a=50 mm\\a = 25 mm$$
$$2b=70.7 mm\\b=35.4 mm$$
となります。
よって、垂直応力は
$\sigma= \frac{F sin45^{\circ}}{\pi ab}\\= \frac{200 N/ \sqrt{2}}{\pi(25mm)(35.4 mm)}=0.05 N/mm^2$$
また、剪断応力は
$$\sigma= \frac{F cos45^{\circ}}{\pi ab}\\= \frac{200 N/ \sqrt{2}}{\pi(25mm)(35.4 mm)}=0.05 N/mm^2$$
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

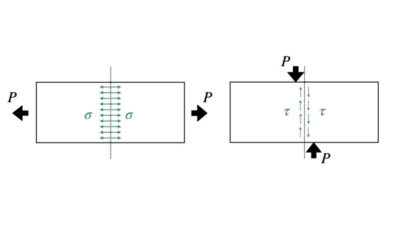
材料に発生する応力の種類【本質的には2種類しかありません】
材料力学の本質:応力とひずみの関係