今回は曲げ応力とはどんな応力なのかについて、概要をさくっとお話しします。
そして、材料(梁)が壊れるかどうかを評価するためには、引張荷重やせん断荷重のときと同様に、荷重を応力に換算しなければなりません。
垂直荷重やせん断荷重から応力を求めるには、ある程度の前提条件はありますが、
基本的には、内力を、仮想断面の面積で割れば求めることができました。
しかし、曲げ応力の場合は、同じように求めることができません。
そこで、今回は曲げ応力について、
そもそもどのような現象なのか?といった導入的な内容に焦点を当てて、
お話しします。
曲げ応力の計算が、垂直応力の計算方法が適用できない理由は
「曲げ」という現象が、引張応力やせん断応力を計算するときの前提とは異なるため、同じように求めることができません。
垂直応力の計算では、次の5つの前提条件がありました。
この中で、垂直応力と曲げ応力とで明確に異なるのは、「仮想断面上で発生する内力が一様であるか、そうではないか」です。
曲げ応力では、仮想断面上で発生する内力は一様ではありません。
結論から言うと、曲げ応力は
引張応力と圧縮応力との組み合わせで成り立っています。
曲げ応力というと、引張応力や圧縮応力とは異なる応力のように見えますが、実際は、曲げ荷重によって発生する引張応力や圧縮応力の総称のことを指しています。
例えば、スポンジのような柔らかい材料を曲げてみます。

すると、
曲げた内側は潰れたように、
曲げた外側は引っ張られるように変形しています。
このことから、材料に曲げ荷重がかかっている時、材料を仮想的に切り離すと、
仮想断面上で、圧縮の部分と、引張の部分とがあると言えます。
つまり、仮想断面上で、内力が一様にはならないことを意味します。
さらに曲げられた材料をよく見てみると、
曲げた内側に行くほど大きく潰れ、
曲げた外側に行くほど大きく引張られます。
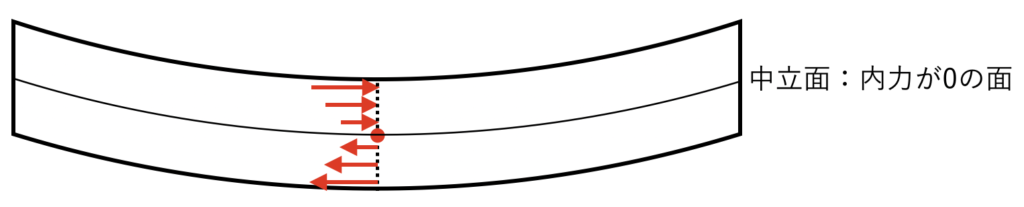
逆に、断面の中の方に行くほど、圧縮や引張の内力が小さくなっていきます。
つまり、仮想断面のどこかに、内力が0になる場所が存在しているのです。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

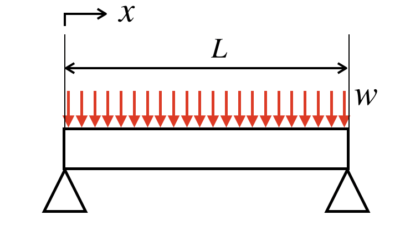
計算を簡略化!等分布荷重のSFD・BMDの書き方
演習問題 04【SFD・BMDの問題】
