今回は、分布荷重の中でも、等分布荷重の場合についてのお話です。
梁の問題は、荷重の分布形態によって、計算の複雑性が異なります。
一般的には、集中荷重に比べて、分布荷重の方が計算が複雑になります。
しかし、分布荷重の中でも、荷重の向きや大きさが一様である「等分布荷重」(材料の自重による荷重など)の場合は、計算を簡単に行うことができます。
今回は、等分布荷重の梁の計算について、
どのように計算をすれば良いのか?
なぜ、そのような計算が使えるのか?
といった内容で、お話ししていきます。
今回も例題を使って解説をしていきます。
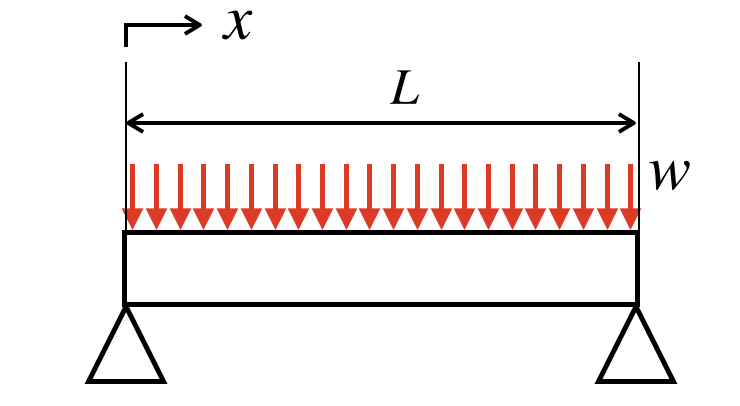
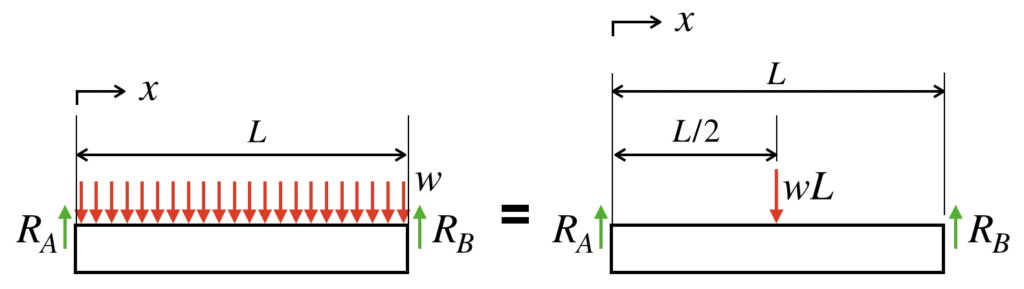
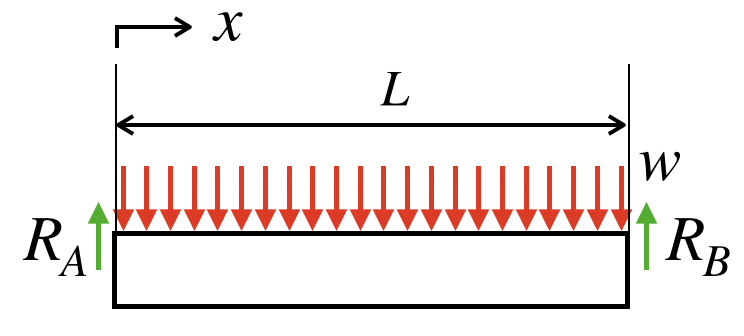
長さLの両端支持梁の全域に、分布荷重wが作用しています。
この梁のSFD・BMDを作成していきます。
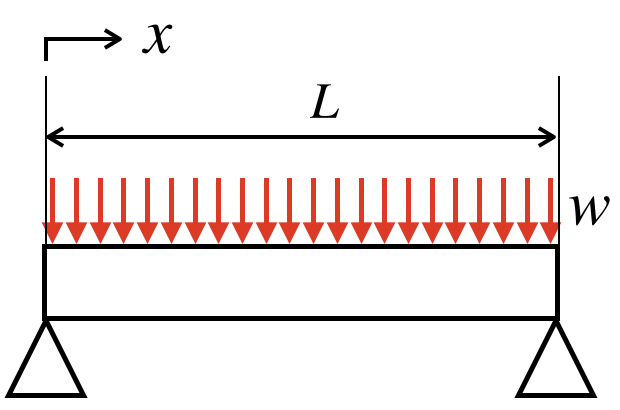
等分布荷重では、分布幅の中の話であれば、梁の位置(xの値)によらず、荷重の大きさや向きが一定です。
例えば、今回の場合は、x=x1の位置でも荷重はwですし、x=x2の位置でも荷重はwです。
この梁は、両端支持梁ですので、反力を描き足すと、以下の図のようになります。
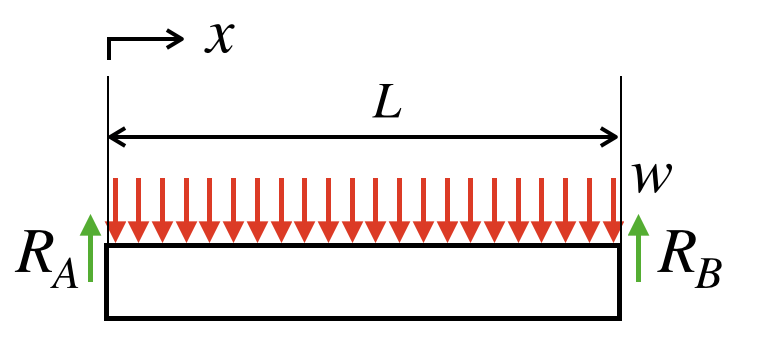
では、釣り合いの式を立てたいのですが、
問題の荷重はどのようになるのでしょうか?
それは、
「分布荷重の合計値が、荷重幅の中央に、集中荷重でかかっているものとしてみなせる」
ということです。
今回の場合、
分布荷重の合計値=wL
荷重幅の中央=L/2
です。
つまり、図で表すと以下の通りになります。
すると、問題はとてもシンプルになります。
まず、釣り合いの式より、反力は以下のとおりになります。
[mathjax]
$$
\begin{cases}
\begin{align}
(上下):&R_A-wL+R_B=0\\
(回転):&wL\cdot \frac{L}{2}-R_BL=0
\end{align}
\end{cases}
\\R_B=\frac{wL}{2}\cdots(1)\\
R_A=\frac{wL}{2}\cdots(2)
$$
続いて、梁を仮想的に切り離します。
等分布荷重の梁を仮想的に離す上で忘れてはいけないのは、等分布荷重の場合はあくまで
「分布荷重の合計値が、荷重幅の中央に、集中荷重でかかっているものとしてみなせる」ということです。
そのため、仮想的に切り離した際は、再度、集中荷重への置き換えについて考えなければなりません。
ここでいう分布荷重の合計値は、wxです(xの位置で仮想的に切り離しているため)。
また、荷重幅の中央は、x/2となります。
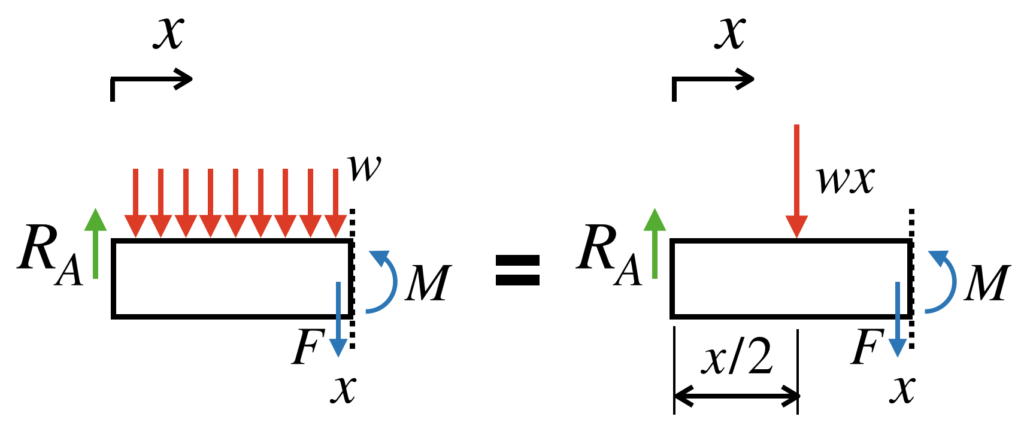
釣り合いについて考えますと、以下のとおりとなります。
$$
\begin{cases}
\begin{align}
(上下):&R_A-F-wx=0\cdots(3)\\
(回転):&wx\cdot \frac{x}{2}-M=0\cdots(4)
\end{align}
\end{cases}
$$
せん断の内力を求めますと、(2)式、(3)式より
$$
\begin{cases}
\begin{align}
&R_A=\frac{wL}{2}\cdots(2)\\
&R_A-F-wx=0\cdots(3)
\end{align}
\end{cases}
\\F=-wx+\frac{wL}{2}\cdots(5)
$$
また、モーメントの内力を求めますと、(1)式、(4)式、(5)式より
$$
\begin{cases}
\begin{align}
Fx-M=0\cdots(4)\\
F=-x+\frac{wL}{2}\cdots(5)
\end{align}
\end{cases}
\\M=-\frac{wx^2}{2}+\frac{wLx}{2}\cdots(6)
$$
となります。
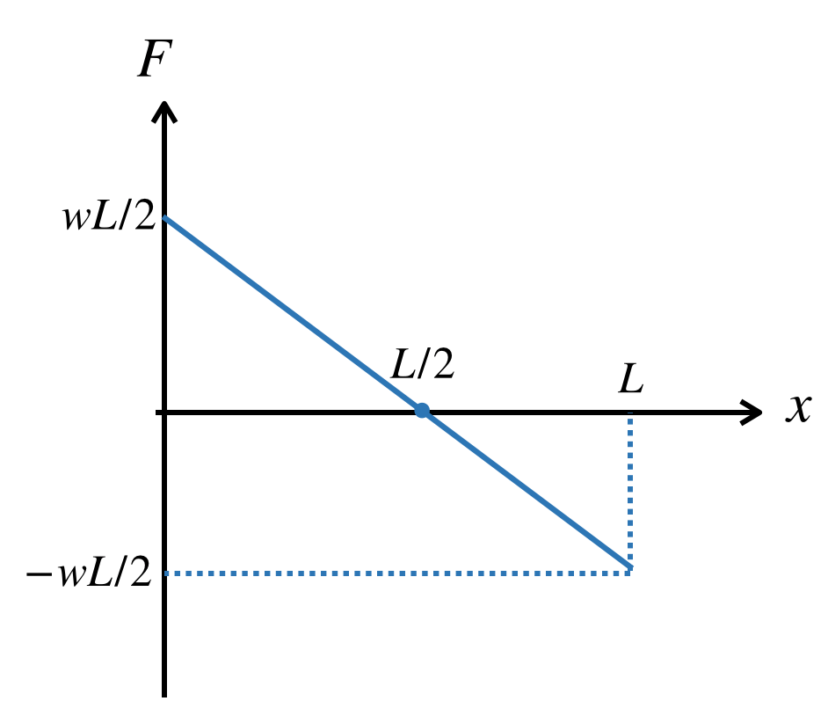
では、SFDから作図していきましょう。
せん断の内力は(5)式より、
$$F=-x+\frac{wL}{2}\cdots(5)$$
です。普通の一次関数ですので、SFDで表すと以下のとおりとなります。
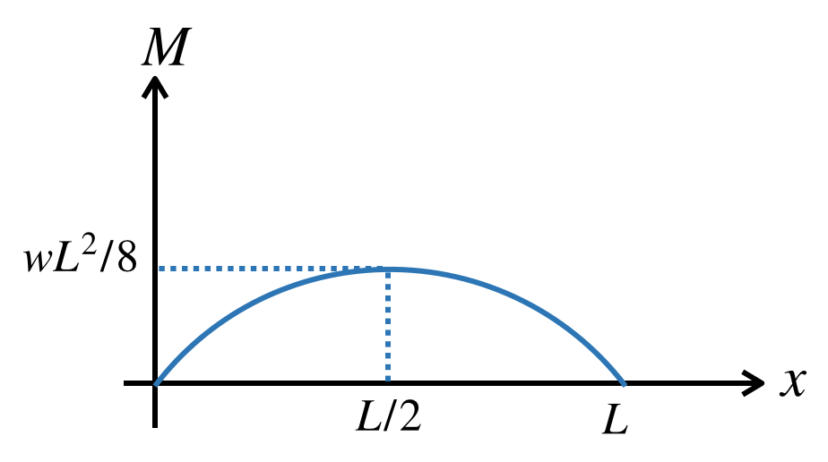
続いて、曲げモーメントの内力は(6)式より
$$M=-\frac{wx^2}{2}+\frac{wLx}{2}\cdots(6)$$
です。これは、上に凸で、頂点がx=L/2である二次関数です。よってBMDは以下のようになります。
このように、等分布荷重の場合では、かなり簡単にSFD・BMDを求めることができるのです。
分布荷重における梁の計算は複雑ですが、なぜ等分布荷重だと集中荷重とみなせるのでしょうか。
その理由について説明するために、等分布荷重での計算を、前回の分布荷重のように、積分を使って計算してみます。
等分布荷重が梁にせん断力として作用するの荷重は、大きさwの荷重をx=0からx=Lまでの区間の合計値となるので、
$$
\int_{0}^{L}wdx=wL
$$
となります。
続いては、等分布荷重が梁にモーメントとして作用する分について考えます。
例えば、x=x1の位置にかかる荷重によって発生するモーメントは、
(荷重w)×(距離x1)なのでwx1となります。
これがx=0からx=Lの区間分までを全て合計した分となります。よって、
$$
\int_{0}^{L}wxdx=\frac{wL^2}{2}=wL\cdot \frac{L}{2}
$$
となります。つまり、荷重wL、位置x=L/2に発生している集中荷重の計算モデルと同じになるのです。
分布荷重ではどうしても積分が絡んできますし、初等関数以外の分布荷重を積分するのは、困難なことが多いです。
今回の等分布荷重の場合のように、少しでも計算をラクにできる知識を知っておくと、かなり便利なので、覚えておくと良いでしょう。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

分布荷重の場合のSFD BMDの書き方
【解説】曲げ応力とは、どんな応力か?