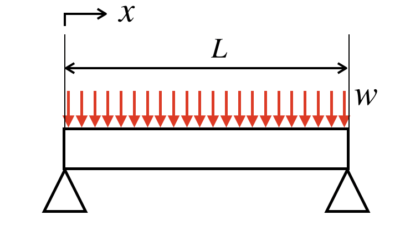
今回は、分布荷重の場合のSFD・BMDについて、お話しします。
分布荷重だからといって、SFDやBMDを書く上での基本的な流れは変わりません。
ただし、分布荷重のSFDやBMDの問題を特には、高校数学の微分・積分の知識が必要となります。
SFDやBMDのグラフが苦手という人は、おそらく分布荷重が入った途端にわからなくなる人が多いと思います。
今回は少し長くなりますが、例題を使いながらじっくりお話していきます。
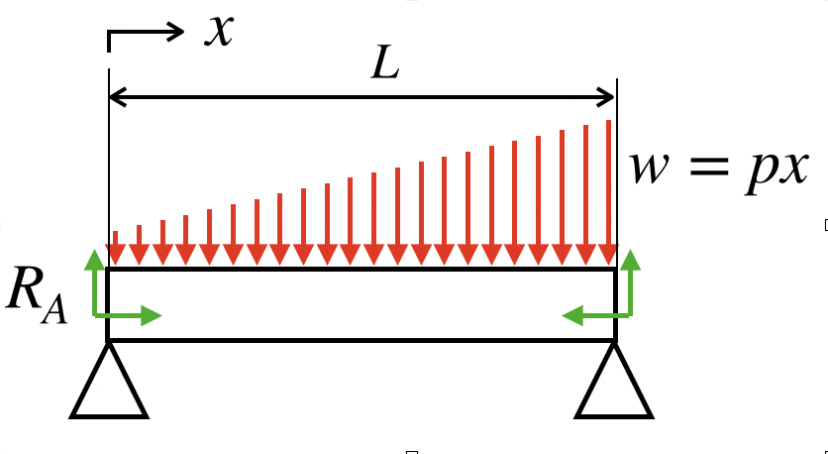
例えば、wが以下の式で与えられるような分布を持っていたとしましょう。
つまり、x=x1の位置における荷重wはpx1となり、x=x2の位置における荷重wはpx2となります。
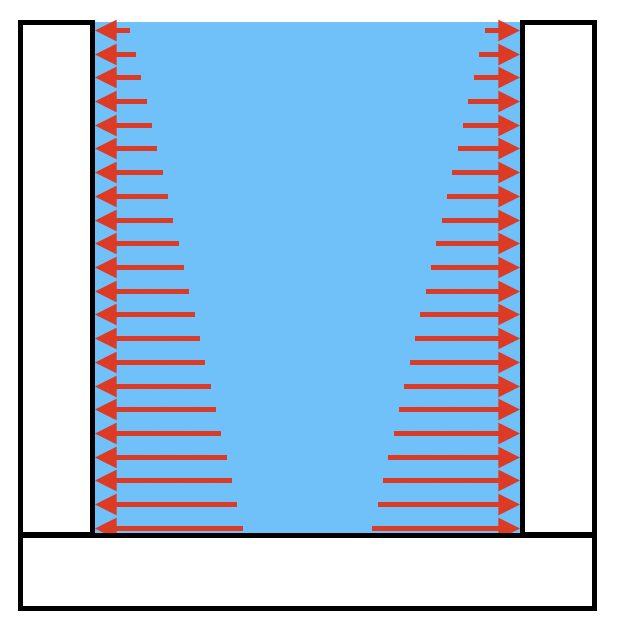
例えば、水族館の水槽の壁が受ける水圧などが、このような荷重の分布をしております。
水深が深くなるほど、水圧が大きくなるためです。
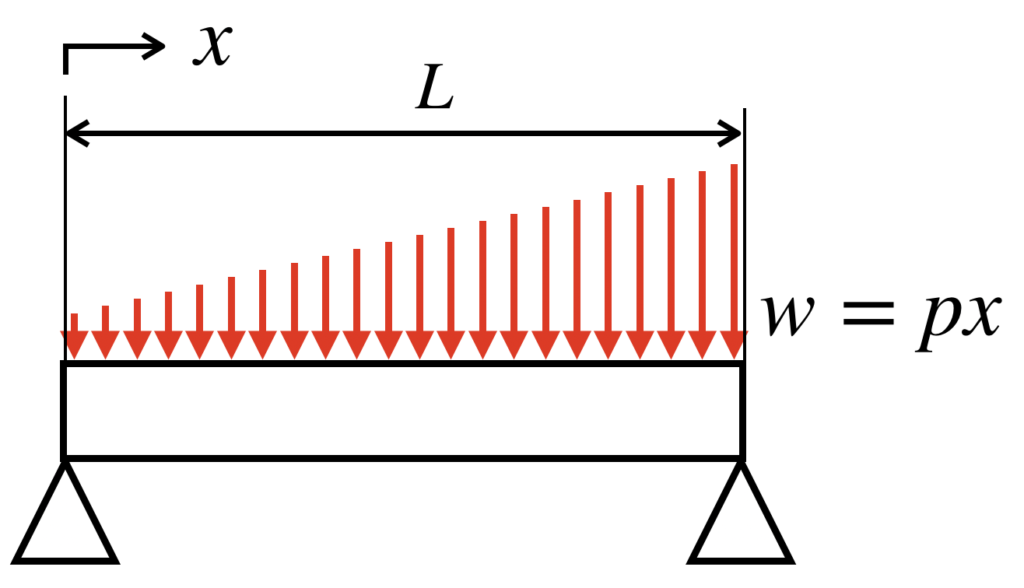
ではまず、この梁について、反力を描き足していきます。
両端支持梁なので、反力を描き足すと、以下のようになります。
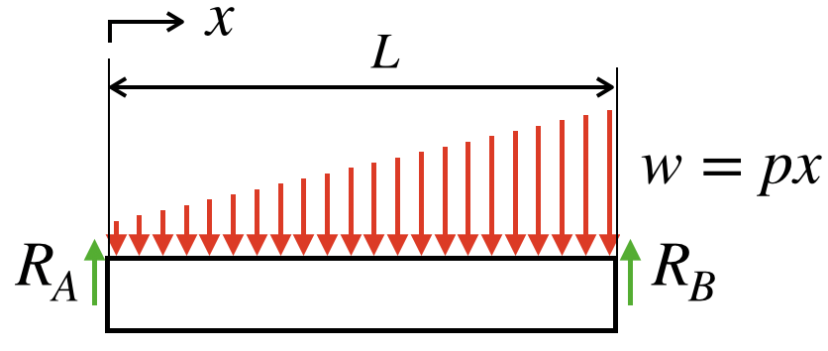
ここで、釣り合いの式を立てたいところではありますが、反力と釣り合う荷重は、どのようになるのでしょうか?
言葉でいうと、各x座標における荷重の大きさを、全て足し合わせたものになります。
つまり、積分を使います。
xの範囲は0からLまでです。よって、釣り合いの式は以下のとおりです。
[mathjax]
$$\begin{align}
(上下方向):&R_A+R_B-\int_{0}^{L}pxdx=0\\
&R_A+R_B-\frac{pL^2}{2}=0\cdots(1)
\end{align}$$
つづいて、モーメントの釣り合いの式についてです。
例えば、x=x1の位置に発生している荷重によるモーメントは、(荷重)×(距離)なので、
$$\begin{align}
px_1\cdot x_1
\end{align}$$
となります。
荷重によるモーメントは、x=0の位置で発生するモーメントから、x=Lの位置で発生するモーメントまでを全て足し合わせたものになります。
よって、モーメントの釣り合いの式は以下の通りとなります。
$$\begin{align}
(回転方向):&\int_{0}^{L}px\cdot xdx-R_BL=0\\
&\frac{pL^3}{3}-R_BL=0\cdots(2)
\end{align}$$
(1)式、(2)式を解くと、
$$
\begin{cases}
\begin{align}
R_A+R_B-\frac{pL^2}{2}=0\cdots(1)\\
\frac{pL^3}{3}-R_BL=0\cdots(2)
\end{align}
\end{cases}
\\R_B=\frac{pL^2}{3}\cdots(3)\\
R_A=\frac{pL^2}{6}\cdots(4)
$$
では続いて、梁を仮想的に切り離してきます。

釣り合いの式を立てると、以下のようになります。
$$
\begin{cases}
\begin{align}
&(上下):R_A-F-\int_{0}^{x}pxdx=0\cdots(5)\\
&(回転):Fx-M+\int_{0}^{x}px\cdot xdx=0\cdots(6)
\end{align}
\end{cases}
$$
積分のところが複雑ではありますが、
上下方向は(荷重px)について、回転方向は(荷重px)×(距離x)について、
それぞれ範囲0からxまで全て足し合わせたものです。
式を見てわからない方は、言葉で理解するのが良いです。
では、内力を求めていきましょう。(4)式と(5)式より、
$$
\begin{cases}
\begin{align}
&R_A=\frac{pL^2}{6}\cdots(4)\\
&R_A-F-\int_{0}^{x}pxdx=0\cdots(5)
\end{align}
\end{cases}
\\F=\frac{pL^2}{6}-\frac{px^2}{2}\cdots(7)$$
また、(6)式、(7)式より
$$
\begin{cases}
\begin{align}
&Fx-M+\int_{0}^{x}px\cdot xdx=0\cdots(6)\\
&F=\frac{pL^2}{6}-\frac{px^2}{2}\cdots(7)
\end{align}
\end{cases}
\\M=-\frac{px^3}{6}+\frac{pL^2}{6}x\cdots(8)\\
$$
となります。
まずはSFDを作図してきます。
縦軸をせん断の内力F、横軸をxとします。Fの式は(7)式より、
$$
F=\frac{pL^2}{6}-\frac{px^2}{2}\cdots(7)
$$
つまり、2次関数のグラフの作図です。これは
$$f(x)=-\frac{px^2}{2}$$
のグラフを、x軸方向に0、y軸方向に(PL2)/6だけ平行移動させたグラフですので、このようになります。
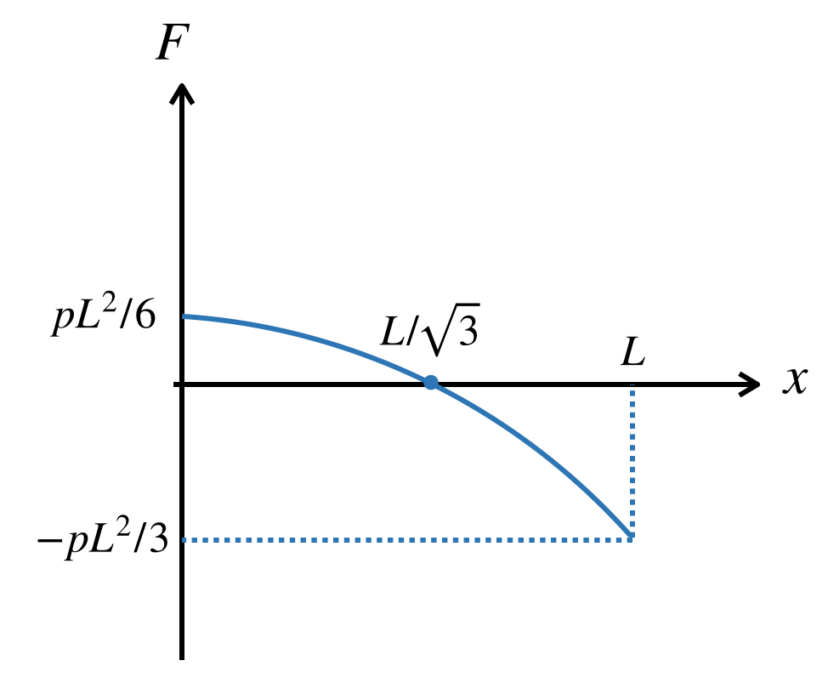
続いて、BMDを作図します。
縦軸をモーメントM、横軸をx軸とします。Mの式は(8)式より
$$
M=-\frac{px^3}{6}+\frac{pL^2}{6}x\cdots(8)
$$
これは3次関数のグラフです。
3次関数のグラフなので、変曲点を調べます。
Mをxで微分したものが0となるxの座標を求めます。
$$
\frac{dM}{dx}=-\frac{px^2}{2}+\frac{pL^2}{6}=0\cdots(9)\\
x=\pm \frac{L}{\sqrt{3}}
$$
また、変曲点でのモーメントは、
$$\begin{align}
M&=-\frac{p}{6}\cdot(\frac{L}{\sqrt{3}})^3+\frac{pL^2}{6}\cdot \frac{L}{\sqrt{3}}\\
&=\frac{pL^3}{9\sqrt{3}}\cdots (10)
\end{align}$$
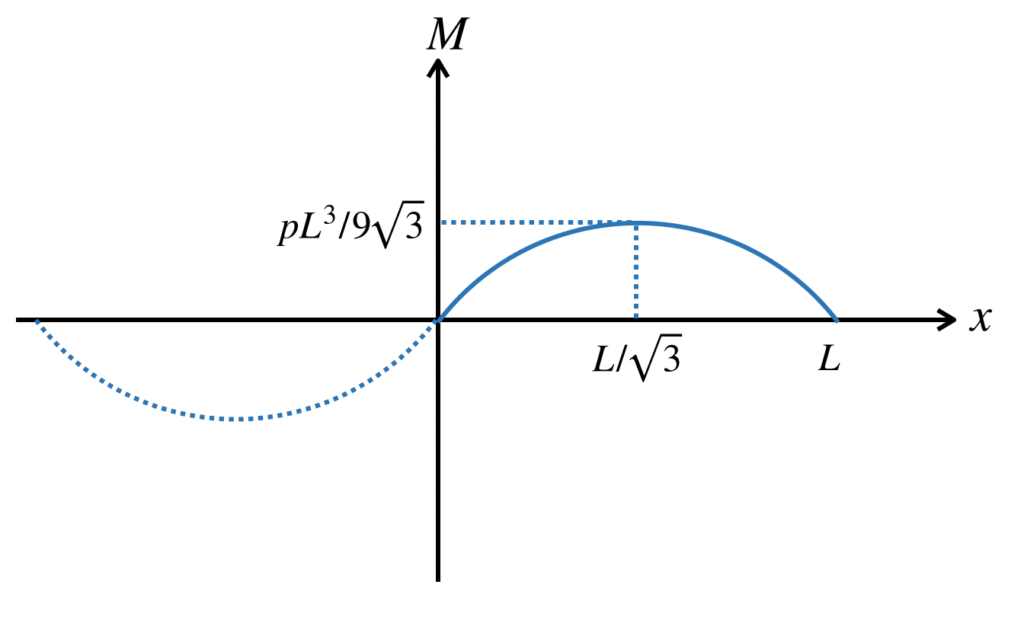
これが答えです。(グラフの左半分のものは、書かなくてもOKです)
集中荷重と分布荷重とでは、基本的な考え方自体は一緒ですが、
分布荷重の方が計算が複雑になるのです。
集中荷重のメリットを、実感できたでしょうか?
最後に、知っておくと便利なことをお教えします。
(7)式と(9)式を見比べて見てください。
$$
F=\frac{pL^2}{6}-\frac{px^2}{2}\cdots(7)\\
\frac{dM}{dx}=-\frac{px^2}{2}+\frac{pL^2}{6}\cdots(9)
$$
そうです。せん断の内力と、モーメントの微分とは同じになります。
このことを知っておくと、BMDの変曲点を求めるのにわざわざ微分しなくても済みますし、
モーメントを求めた際の計算が合っているかどうかの検算にもなります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

梁にかかる荷重と、SFD・BMDの作り方
計算を簡略化!等分布荷重のSFD・BMDの書き方