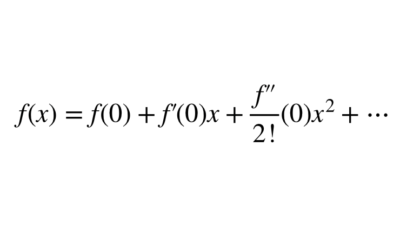
今回はラジアンをイメージする方法についてお話しします。
高校数学で、角度の表記方法として「ラジアン」が出てきますが、
日常生活で角度を表す時に、一般的には「度」を使うことが多いため、私はとても馴染みにくかったです。例えば突然「1.7ラジアン」と言われても、それがだいたいどの程度の角度なのかが想像できません。
一応、度とラジアンの変換式はあります。
正確な計算をする上ではちゃんと式を利用するべきですが、
ザックリとした角度の大きさのイメージを掴みたいだけなのに、ラジアンが出てくる度に変換式を使っていては、とても煩わしいです。
そこで今回は、ラジアンから角度をイメージできるためのコツについて、お話ししていきます。
ラジアンは、半周でπ、一周で2πです。
これを基準として覚えておくのがコツです。
私は最初にピザをイメージしています。
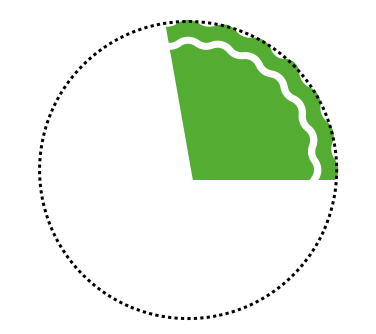
例えば「π/3」と言われた場合は、「ピザを半分に切った後に3等分する」といった具合にイメージをします。

私は3人兄弟で、子供の頃はご飯やお菓子を基本的に兄弟で分け合って食べていたので、このイメージはとても使いやすいと感じております。
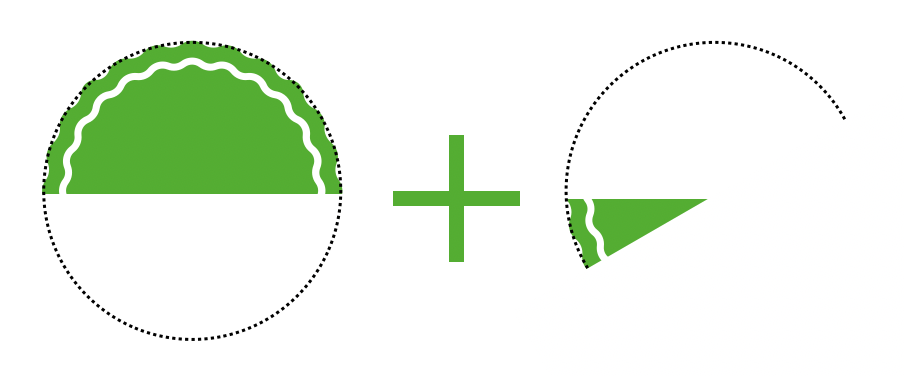
「7π/6」と言ったように、πの値を超えている場合は、「π+π/6」と言ったようにすると、
「ピザ半分」と「半分を6等分した分の角度」といった具合にイメージします。
度で表すと、180度+30度=210度
学校で習うラジアンの値は、nπ/6、nπ/4、nπ/3、nπ/2、nπの5種類です。
(それぞれ度に直した時に、n×30°、n×45°、n×60°、n×90°、n×180°となるので、扱いやすいですからね)
しかし、ピザのイメージを使えば、
例えば4π/7ラジアンと言われても、それが鋭角なのか鈍角なのかはすぐわかります。
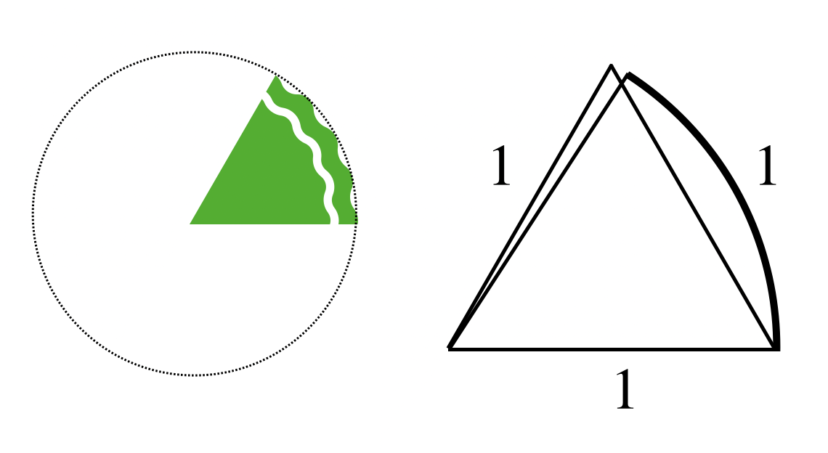
πがついていないようなラジアンの場合、正三角形をイメージするのがよいです。
例えば1ラジアンとは、半径が1の扇型の孤の長さが1という意味です。
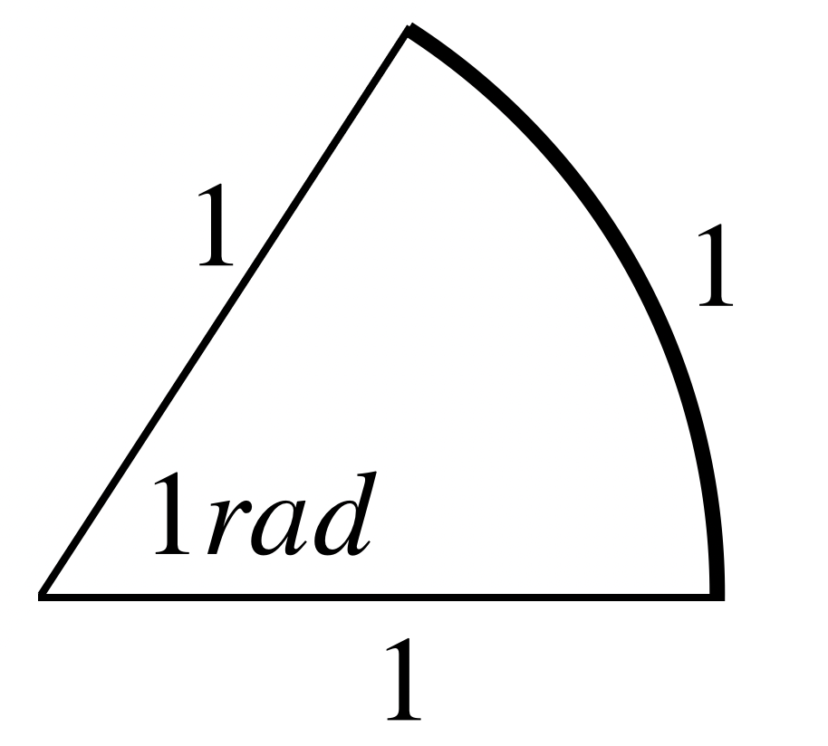
この図形と近いものが、一辺が1の正三角形となります。
1ラジアンの扇型と、正三角形との違いは、辺の1つが、円弧なのか扇型なのかの違いです。
もちろん、扇型の方が角度が浅くはなります。
(1rad=約57度、正三角形の角度=60度)
ですが、ざっくりとした角度のイメージであれば、正三角形とだいたい一緒としてもOKです。
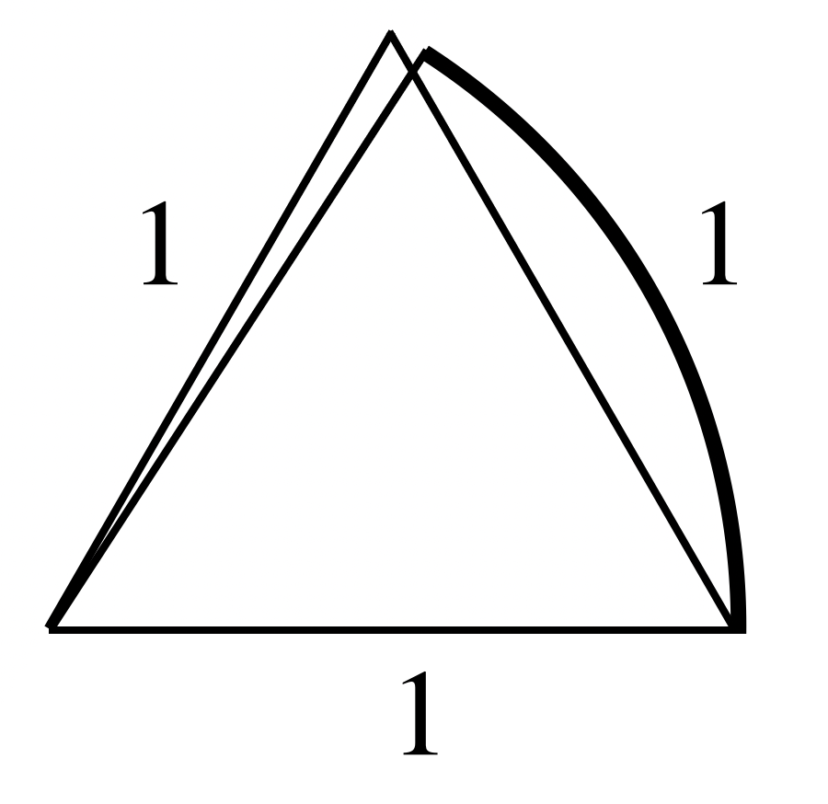
よって、
$$1rad\approx\frac{\pi}{3}rad$$
つまり、冒頭の1.7ラジアンは、鈍角になります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


Q.「ラジアン」とは何か? A.「角度」や「円弧の長さ」を表すもの
テイラー展開の公式集