テイラー展開の公式集

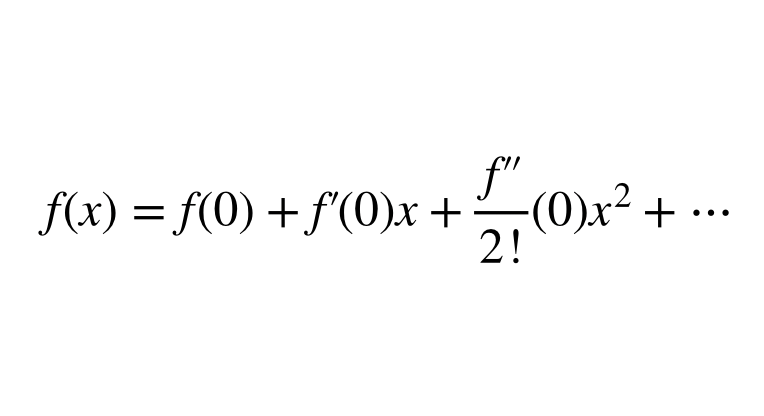
さまざまな関数についてのテイラー展開の公式を掲載します(a=0まわりの展開であるため、マクローリン展開とも言います）

しかし、できるだけ、公式の丸暗記ではなく、原理を覚えることをオススメします。

原理自体あまり難しくなく、さらにその原理さえ覚えてしまえば、一つ一つの公式について暗記をする必要がないためです。

マクローリン展開

$$f(x)=f(0)+f^{\prime}(0)x+\frac{f^{\prime\prime}(0)}{2!}x^2+\cdots+\frac{f^{k}(0)}{k!}x^k+\cdots$$

$$sinx=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\\$$

$$cosx=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots\\$$

$$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots$$

$$log(x+1)=1+x+\frac{x^2}{2}+\frac{x^3}{3}\cdots$$

ただし、-1<x≦1

$$(1+x)^n=1+nx+\frac{1}{2!}n(n-1)x^2+\cdots+\frac{1}{k!}(n(n-1)\cdots(n-(k-1))x^k\cdots$$