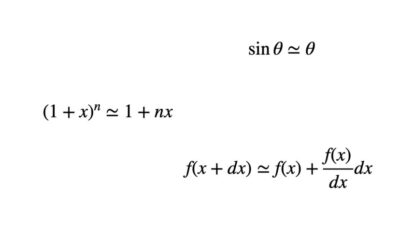変数分離とは、微分方程式を解くためのテクニック・手法のことをいいます。
大学で習うような物理の問題では、微小要素に分割し、全体を積分する方法で解くことが多いです。
その際には、式中に微分(導関数)を含む方程式である「微分方程式」を解く必要があります。
そしてその解き方としてよく見かけるのが「変数分離」と呼ばれる手法です。
変数分離自体は、大学になってから習うことがあると思いますが、高校生の人でも覚えておくと、納得をしながら物理を勉強できます。
そんな変数分離について、今回はお話ししておきます。
微分方程式にはたくさんのパターン(型)の方程式がありますが、実は多くの場合、未だに解くことができません。
しかし、解けることが証明されている微分方程式が少しだけあり、中でもよく登場するのが「1階常微分方程式」と呼ばれるパターンです。
まず「1階」というのは、微分を1回したという意味です。
数学では方程式に名前をつけるときに、式に登場する微分の項のうち、最も多く微分されているものを代表して「n階微分方程式」と呼びます。
中学校で習う1次方程式、2次方程式も、xの次数が最も多いものを代表して「n次方程式」と読んでいますね。
これと似たような呼び方をしていると思っていただくのがいいかと思います。
続いて「常微分方程式」というのは、独立変数が1つだけの微分方程式のことを言います。
独立変数というのは、関数の値を確定させるために決定させる必要がある変数のことで、
例えば「z=2y+x」という関数は、xの値と、yの値の2つを決定させないとzの値を確定させることができませんので、独立変数の数は2つということになります。
つまり、1階常微分方程式とは、
という意味になります。
変数分離での解き方は主に以下のステップとなります。
$$q(y)dy=p(x)dx\\
\int q(y)dy=\int p(x)dx+C$$
2のステップで「yの定数項は?」と 思った人もいるかもしれませんが、yの定数項とxの定数項をまとめて「C」としていると考えれば納得できるかと思います。
例題をやって見ましょう。
y'(x)=xy2を解いていきます。
y'(x)をdy/dxと書きなおして、左辺と右辺とでそれぞれ変数をわけていきます。
$$\begin{align}
y'(x)&=xy^2\\
\frac{dy}{dx}&=xy^2\\
\frac{dy}{y^2}&=xdx\cdots(1)
\end{align}$$
続いて、それぞれの変数で積分をしてきます。
$$\begin{align}
\int\frac{dy}{y^2}&=\int xdx\\
-\frac{1}{y}&=\frac{1}{2}x^2+C
\end{align}$$
これが、微分方程式の答えとなります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

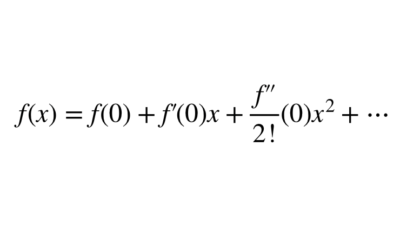
テイラー展開の公式集
【解説】機械工学系の学問でよく使う近似式