【解説】機械工学系の学問でよく使う近似式

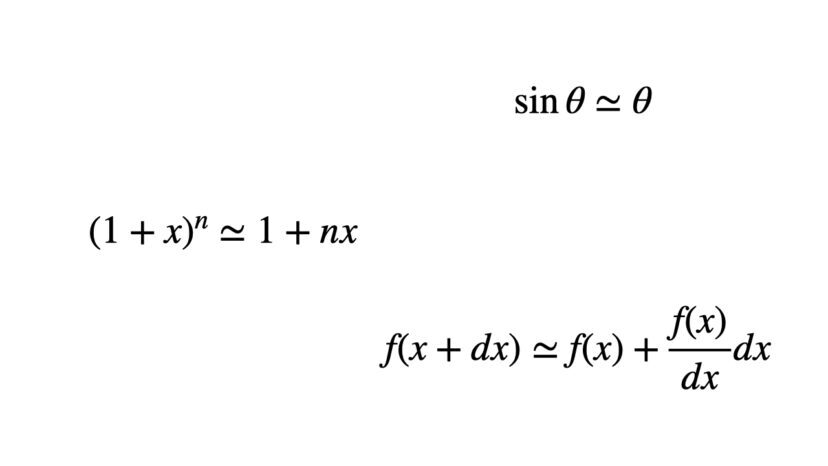
こんにちは、リヴィです！

今回は主に大学生向けの記事です。

大学で機械系の授業を受けていると、

あれ、なんか高校のときにやっていた微分・積分と雰囲気が違うぞ？急に授業についていけなくなってきた・・・

ということが起こりやすくなります。

高校までは学校の先生は丁寧に教えてくれるという感じなのですが、大学の先生は「教育のプロ」というよりも「研究のプロ」なので、「わかりやすい授業」というのは激減します。

どちらかというと、「こういうの知ってて当たり前だよね？」みたいな感じで、ガンガン授業が進んでいきますよねー笑

特に機械系の授業およびその後の研究では、新しく習う「微分方程式」をガンガン使うことが多いのですが、裏を返せば、一度置いていかれると学校の授業についていけなくなってきます。

また、微分方程式を得く上では、さまざまな近似式を使うのですが、どういった用途で使えるものなのかを知っていないと、なかなか頭に入っていきません。

そこで今回は、機械工学系の学問でよく使われる近似式について、例題も交えて解説してきます。

なお、近似式の導出の導出で使われる「テイラー展開」については、以下の記事で解説していますので、よろしければご参照ください。

力学で出てくるテイラー展開と近似【式の導出でよく使います】

大学の工学・力学の授業で、いろんな式の導出を習っているけれど、特に「微小な値」とか「十分に小さい」とか言って、いきなり式が近似されるのがイマイチ納得できない。 このような疑問・悩みを持った人へ、お答え…

https://rivi-manufacturing.com/mechanics/4584

指数

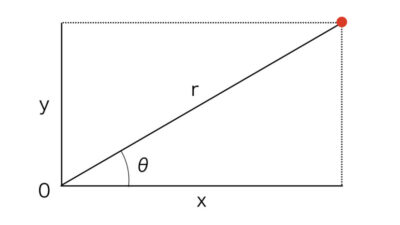
|x|<<1(xの絶対値が1より十分に小さい）のとき、

• $$1+x^2\simeq1$$
• $$1+x^3\simeq1$$
• $$\sqrt{1+x}\simeq 1+\frac{x}{2}$$
• $$(1+x)^n \simeq 1+nx$$
• $$e^x \simeq 1+x$$

例題：スライダリンクの運動

これらの式を使う上でよく目にするのは、スライダリンクの問題とかです。

【問題】

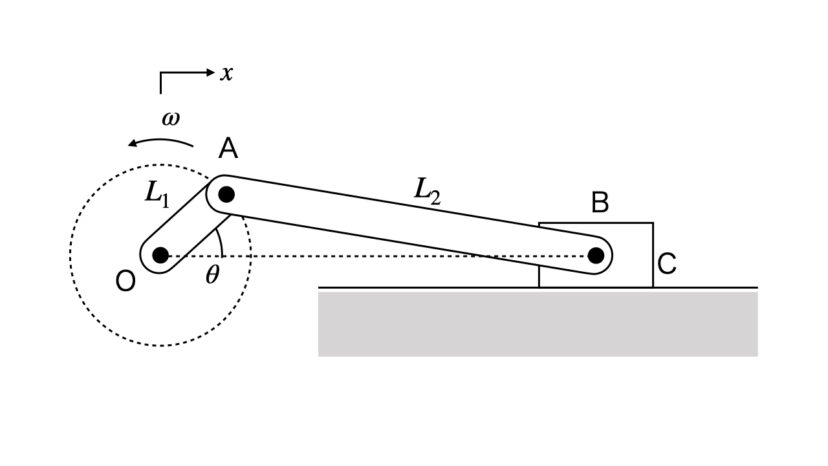
以下の図のスライダリンク機構において、OAおよびABがリンクで接続されており、BにスライダCが接続され、スライダCはOを通る直線上を動くよう拘束されている。

∠BOAをθ、OAの角速度はωで一定、OAの長さをL₁、ABの長さをL₂で、L₁ <<L₂のとき、加速度aは以下の式で求められることを示せ。

$$a=-L_1\omega^2\cos\theta-\frac{L_1^2}{L_2}\omega^2\cos2\theta$$

【解答】

問題文の「L₁<< L₂」のような記述を見た時、「あ、L₁/L₂っていう形にできたら、微小量にできそうだな！」という勘が働くと、問題をどう解けばよいかすぐわかりますね！

AからOBに垂線を引きその交点をPとします。

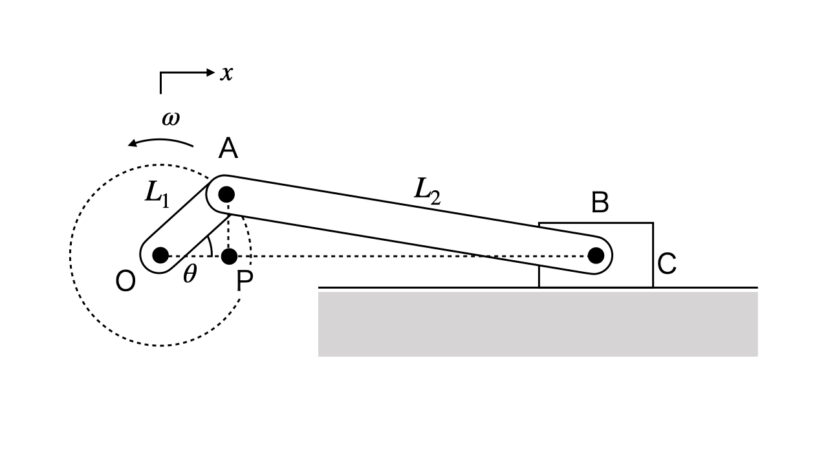
スライダCの位置xは、三角関数、三平方の定理を使って、

$$\begin{align}OB=x&=OP+PB\\
&=OA\cos\theta+\sqrt{AB^2-OA\sin^2\theta}\\
&=L_1\cos\theta+\sqrt{L_2^2-L_1^2\sin^2\theta}\end{align}$$

となります。

次にこの式をうまく整理して、「L₁/L₂」という形に持っていきたいと思います。

平方根の中を整理すると、

$$\begin{align}x&=L_1\cos\theta+\sqrt{L_2^2-L_1^2\sin^2\theta}\\
&=L_1\cos\theta+L_2\sqrt{1-\left(\frac{L_1}{L_2}\sin\theta\right)^2}\\
&=L_1\cos\theta+L_2\left(1-\left(\frac{L_1}{L_2}\sin\theta\right)^2\right)^{1/2}
\end{align}$$

ここで、

$$\sqrt{1+x}\simeq 1+\frac{x}{2}$$

を適用すると

$$\begin{align}
x&=L_1\cos\theta+L_2\left(1-\left(\frac{L_1}{L_2}\sin\theta\right)^2\right)^{1/2}\\
&\simeq L_1\cos\theta+L_2\left(1-\frac{1}{2}\left(\frac{L_1}{L_2}\sin\theta\right)^2\right)\\
&=L_1\cos\theta+L_2-L_2\frac{1}{2}\left(\frac{L_1}{L_2}\sin\theta\right)^2\cdots (1-1)
\end{align}$$

となります。

速度vは(1-1)式を時間で微分をすれば答えが導き出されます。

このとき、sinθやcosθの時間微分では合成関数の微分をするということに注意をして、

$$\begin{align}
v&=L_1\frac{d}{dt}\cos\theta-L_2\frac{1}{2}\frac{d}{dt}\left(\frac{L_1}{L_2}\sin\theta\right)^2\\
&=L_1\frac{d\cos\theta}{d\theta}\frac{d\theta}{dt}-L_2\frac{1}{2}\frac{d}{d\theta}\left(\frac{L_1}{L_2}\sin\theta\right)^2\frac{d\theta}{dt}\\
&=-L_1\omega\sin\theta-\frac{L_1^2}{2L_2}\omega2\sin\theta\cos\theta\\
&=-L_1\omega\sin\theta-\frac{L_1^2}{2L_2}\omega\sin2\theta
\cdots (1-2)
\end{align}$$

よって加速度aは(1-2)式を時間で微分して求めていきます。

$$\begin{align}
a&=\frac{d}{dt}(-L_1\omega\sin\theta)-\frac{d}{dt}\left(\frac{L_1^2}{2L_2}\omega\sin2\theta\right)\\
&=-L_1\omega^2\cos\theta-\frac{L_1^2}{L_2}\omega^2\cos2\theta
\cdots (1-3)
\end{align}$$

三角関数

θ（θはラジアン）が十分に小さい時、

• $$\sin\theta\simeq\theta$$
• $$\cos\theta\simeq1$$
• $$\tan\theta\simeq\theta$$

式の導出についてはこちらに記載しています。

例題：振り子の周期

【問題】

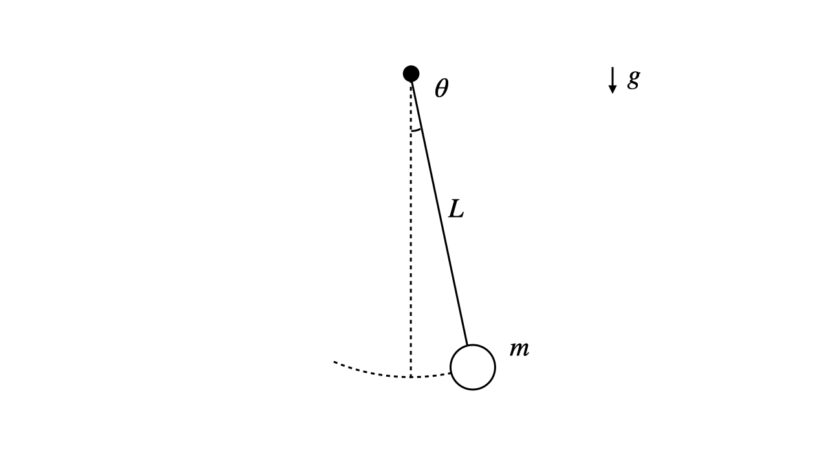
以下の図のように、長さLの伸び縮みしない糸の一端が点Oに固定され、もう一端に質量mの重りがぶら下がっている。

振れ角θ₀のときにおもりを静かに離して振り子運動をさせたとする。

鉛直下方からの振れ角θ、重力加速度をgとするとき、振り子の周期Tを求めよ。

ただし、糸の質量は無視するものとする。

【解答】

まず、以下の図のように、おもりに対して、半径方向と円周方向にr-θ座標を設置し、座標に沿って力のベクトルを分解します。

今回は振り子の周期を求めるので、θ方向の力について注目し運動方程式を立てます。

2次元極座標

$$\begin{align}m\left(r\frac{d^2\theta}{dt^2}+2\frac{dr}{dt}\frac{d\theta}{dt}\right)=-mg\sin\theta\cdots(2-1)\end{align}$$

ちなみに、半径方向の力の関係について式を立てると「糸の張力」が求まります。

(2-1)式の両辺をmで割り、r=L、糸は伸び縮みしないことを考慮すると、

$$\begin{align}\frac{d^2\theta}{dt^2}=-\frac{g}{L}\sin\theta\cdots(2-2)\end{align}$$

となります。

ここで、θが微小ならば、

$$\sin\theta\simeq\theta$$

と近似できるので、これを(2-2)式に代入すると、

$$\begin{align}\frac{d^2\theta}{dt^2}=-\frac{g}{L}\theta\cdots(2-3)\end{align}$$

ここで、

$$\omega=\sqrt{\frac{g}{L}}$$

とすると、(2-3)式は

$$\begin{align}\frac{d^2\theta}{dt^2}=-\omega^2\theta\cdots(2-4)\end{align}$$

となり、単振動と同じ式となります（ωは、単振動でいう角振動数）。

よって周期Tは

$$T=\frac{2\pi}{\omega}=\sqrt{\frac{2\pi L}{g}}$$

となります。

この問題のようにθが十分に小さい振り子の運動は単振動とみなせることから「単振り子」と呼ばれたりします。

微小要素

dx、dyが微小である時

• $$f(x+dx)\simeq f(x)+\frac{f(x+dx)}{dx}dx$$
• $$f(x+dx,y+dy)\simeq f(x,y)+\frac{\partial f(x,y)}{\partial x}dx+\frac{\partial f(x,y)}{\partial y}dy$$

【例題】

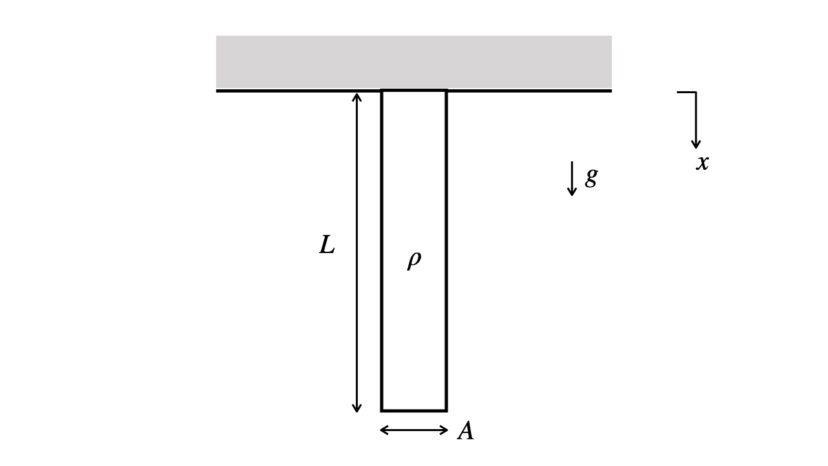
下の図のように、天井に一様な丸棒が垂直に固定されています。

丸棒の長さ・断面積・密度をそれぞれL・A・ρ、重力加速度をg、丸棒と天井との固定部を原点として鉛直下向きにx軸を設定したとき、丸棒に働く内力の大きさを求めてください。

【解答】

初級編の材料力学のように、テキトーなところで棒を仮想的に切って、力の関係から内力を求めることもできるのですが、

応用問題にも適用できるようになるために、今回解説するような「微小要素に切り分けて、微分方程式を解く方法」でもできるようにしておきましょう。

まず、丸棒を長さdxの微小な要素に切り分けていきます。

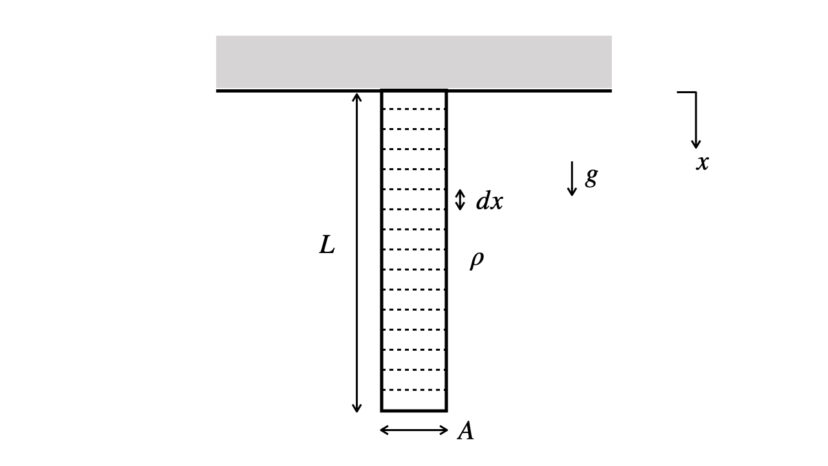
この「dx」ですが、「d×x」ではなく「dx」で1つの文字として捉えてください。

これらのうち、テキトーな位置にある微小要素を取り出して考えてみます。

微小要素の上端の座標は「x」、下端の座標は「dx」となります。

微小要素の上端・下端は、もともとは各隣の微小要素とくっついていたことから、内力Fが発生しています。

よって図で表すと

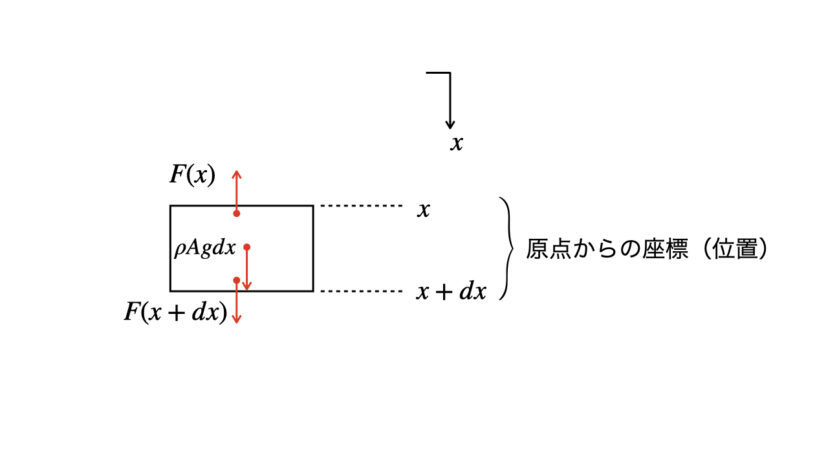
赤矢印を元にして式で表すと、以下の通りとなります。

$$F(x+dx)-F(x)+\rho A(dx)g=0\cdots(3-1)$$

ここで内力Fはxの位置によって値が変わる（xの関数である）ので、F(x)およびF(x+dx)とします。

ここで、以下の式を適用してきます。

$$F(x+dx)\simeq F(x)+\frac{dF(x)}{dx}dx$$

すると(3-2)式は、

$$F(x)+\frac{dF(x)}{dx}dx-F(x)+\rho Ag(dx)=0\\
\frac{dF(x)}{dx}dx+\rho A(dx)g=0\\
\frac{dF(x)}{dx}=-\rho Ag\cdots(3-3)$$

となります。

この形の微分方程式は、変数分離という方法で解けます。

(3-3)式の両辺にdxをかけて積分すると、

$$\begin{align}
dF(x)&=-\rho Agdx\\
F(x)&=\int(-\rho Ag)dx\\
&=-\rho Agx+C\cdots(3-4)
\end{align}$$

ここで、問題の図に注目すると、丸棒の先端には荷重が何もかかっていないことがわかります。

つまり、x=Lの場所で、F(x)=0となります（これを境界条件と言います）。

よって、この境界条件を(3-4)式に代入すると、

$$0=-\rho AgL+C\\
C=\rho AgL$$

よって内力は、

$$\begin{align}
F(x)&=-\rho Agx+\rho AgL\\
&=\rho Ag(L-x)
\end{align}$$

となります。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...