
世の中にはものの「角度」を表す方法は主に2種類あります。
1つ目は皆さんが義務教育で習う表し方で「度数法」と呼ばれているものです。
単位としたは「度」や「°」を使うものです。
もう1つは「弧度法」と呼ばれているもので、これは高校数学にて登場するもので、単位として「ラジアン」を使うものです。
この「ラジアン」というのは、高校数学で唐突に出てきますが、
日常生活をする上では、ほとんどラジアンが登場することがなく、なかなか馴染めないことが多いと思います。
実はラジアンには、以下の2つの捉え方があります。
そこで、ラジアンについて、
日本語としての理解ではなく、
頭の中で理解ができるように、今回は解説をしていきます。
ラジアンは一周を2πとして表すものです。
なぜ一周が2πなのか?
それは、円周の長さに由来します。
円周の長さを求める式は、(直径)×(円周率)です。
半径が1の円を考えると、円周は、
$$2\times1\times\pi$$
です。だから「一周=2π」となるのです。
ちなみに、ラジアンと度の変換は以下のとおりです。
[mathjax]
$$1[deg]=\frac{2\pi}{360}\\ 1[rad]=\frac{360}{2\pi}$$
ラジアンはよく、三角関数(sinやcos)で登場するため、こちらの認識を持たれている方が多いと思います。
何故、孤の長さで角度を表せるのか?
それは、半径が1だと決まっているからです。
角度を表すには、直接的に表さなくとも、
図形の形と長さを決めるだけで、その図形が作る角度を「ただ一つに」決めることができます。
例えば孤の長さがxラジアンだとすると、半径が1で孤の長さがxと決まっているので、それを満たすような扇型の中心角は1種類しか存在しません。
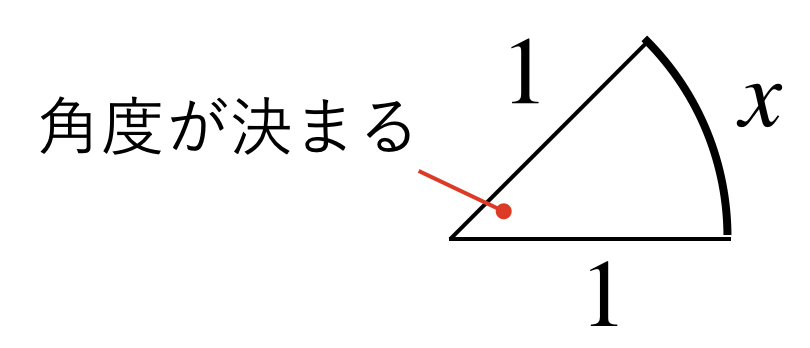
また例えば、三角形の1つの角がxラジアンという意味は、
「その角度が、半径が1で孤の長さがxである図形の中心角が作る角度に相当する角度」という意味です。
もう一つ、ラジアンの使い方として「弧の長さ」を表すというものがあります。
これは、先ほどの角度の発想とは逆です。
つまり、半径が1の扇型の角度がわかっていれば、孤の長さがわかるということです。
これは、材料力学の梁の問題でも使われる、考え方です。
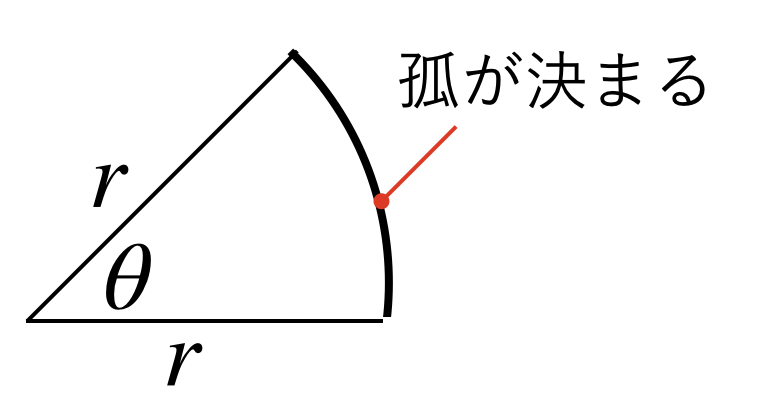
孤の長さを求めるには、半径×ラジアンで求めることができます。
また、xが微小である時、
$$\sin{x}=x$$
とすることができる。
この考え方は「度」表記ではできません。
半径が1で、角度がπ/2rad(90度)の扇型の孤の長さは、
π/2ではありますが、90ではないのは明らかです。
数学でラジアンがよく使われるのは、度に比べて使い勝手がいいというのもあります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

ラジアンをイメージする方法
