材料力学 演習問題 03【熱応力】

不静定や熱応力の問題はつまづきやすいポイントです。

特に熱応力の問題は、一見すると、教科書の説明を見る限りは大したことがなさそうなのですが、いざ問題を解こうとすると、ペンが進まないといったことがよくあります（多くの場合は不静定問題と絡んでいます）。

問題は2問だけですが、つまづきやすいがために、少しハードルは高めです。

今回の演習で、問題が解けるようにマスターしておきましょう。

問題

問1

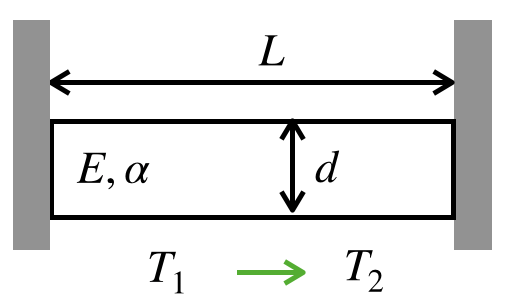
下図のように、温度T₁の環境において、直径d、長さL、ヤング率E、線膨張係数αである丸棒の両端が断熱壁に固定されており、棒材間は隙間なく接触しています。

この状態から温度をT₂へ変化させた時、棒材に発生する応力を求めてください。

答え

問2

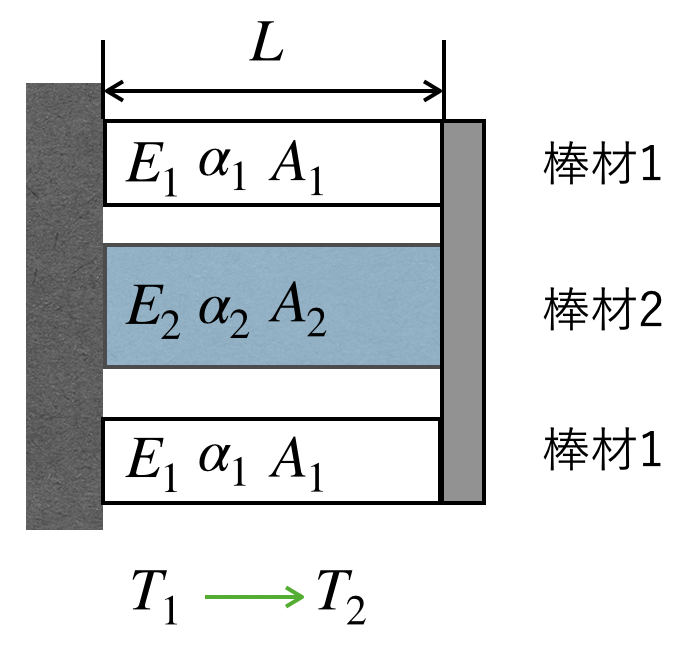
下図のように、温度T₁の環境において、断面積A₁、長さL、ヤング率E₁、線膨張係数α₁である棒材1が2本と、断面積A₂、長さL、ヤング率E₂、線膨張係数α₂である棒材2が1本の左端が断熱壁に、右端が断熱板に固定されています。

この状態から温度をT₂まで上昇させた時、各棒材に発生する応力を求めてください。

答え

答え

問1

まずこの問題を見たときに「両端が壁に固定されている＝不静定問題」と気づけるとよいですね。

では、どこから手をつけるかですが、まずは問題を別のとらえ方で見てみます。

つまり、「熱膨張するはずの棒が、壁によって拘束されているから変形できない」という発想を、「熱膨張した状態の棒が、壁の反力によって圧縮荷重を受けて変形した」という発想に変換します。

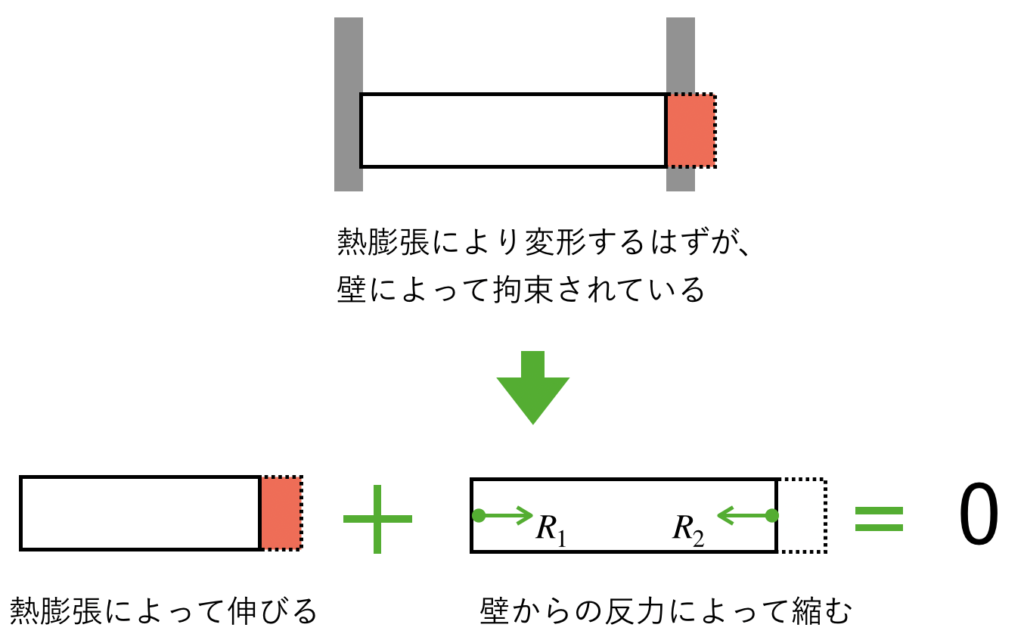
ここから、変形量に着目し「熱による変形量＋荷重による変形量」=0という式を立てます。

熱による変形量は、

$$\begin{array}{rl}\mathrm{\Delta }{L}_T& ={\epsilon }_{T}L\\ & =\alpha (T_2-T_1)L\cdots (2)\end{array}$$

荷重による変形量は次の流れで求めます。

1. 内力をFと置く（初心者はここから計算するのがオススメ）
2. 棒を仮想的に切り離し、釣り合いの式を立てる。
3. 応力を表す
4. フックの法則からひずみを求める（材料に発生する現象がイメージできる人はここから式を立ててもOK）
5. ひずみから変形量を求める

内力をFとおいて、棒を仮想的に切り離し、釣り合いの式を立てると、

$$\begin{array}{rl}{R}_1-F& =0\\ F& =R_1\end{array}$$

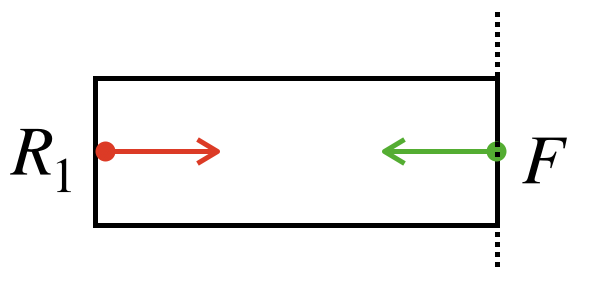
ここから、応力の定義より、

$$\begin{array}{rl}\sigma & =\frac{F}{\pi d^2/4}\\ & =\frac{R_1}{\pi d^2/4}\end{array}$$

フックの法則より、

$$\begin{array}{rl}{\epsilon }_F& =\frac{\sigma }{E}\\ & =\frac{R_1}{E\pi d^2/4}\end{array}$$

よって、荷重により変形量は、

$$\begin{array}{rl}\mathrm{\Delta }{L}_F& ={\epsilon }_{F}L\\ & =\frac{R_{1}L}{E\pi d^2/4}\cdots (3)\end{array}$$

(1)に、(2)と(3)を代入すると、

$$\begin{array}{r}\mathrm{\Delta }{L}_T+\mathrm{\Delta }{L}_F=0\\ \alpha (T_2-T_1)L+\frac{R_{1}L}{E\pi d^2/4}=0\\ R_1=-\frac{E\pi d^2}{4}\cdot \alpha (T_2-T_1)\end{array}$$

つまり、「熱膨張によって、棒はR₁に相当する圧縮荷重を受けている」ということができます。

よって、熱応力は、

$$\begin{array}{rl}\sigma & =\frac{F}{\pi d^2/4}\\ & =\frac{R_1}{\pi d^2/4}\\ & =-E\alpha (T_2-T_1)\end{array}$$

これが答えです。

補足ですがこの方法は、材料に発生してる現象をイメージできるように、「内力を求めてから、応力を求める」という説明をしております。

現象のイメージができているという人は、(3)式を

$$\mathrm{\Delta }{L}_F=\frac{\sigma L}{E}$$

とすると、手間が省けます。

問2

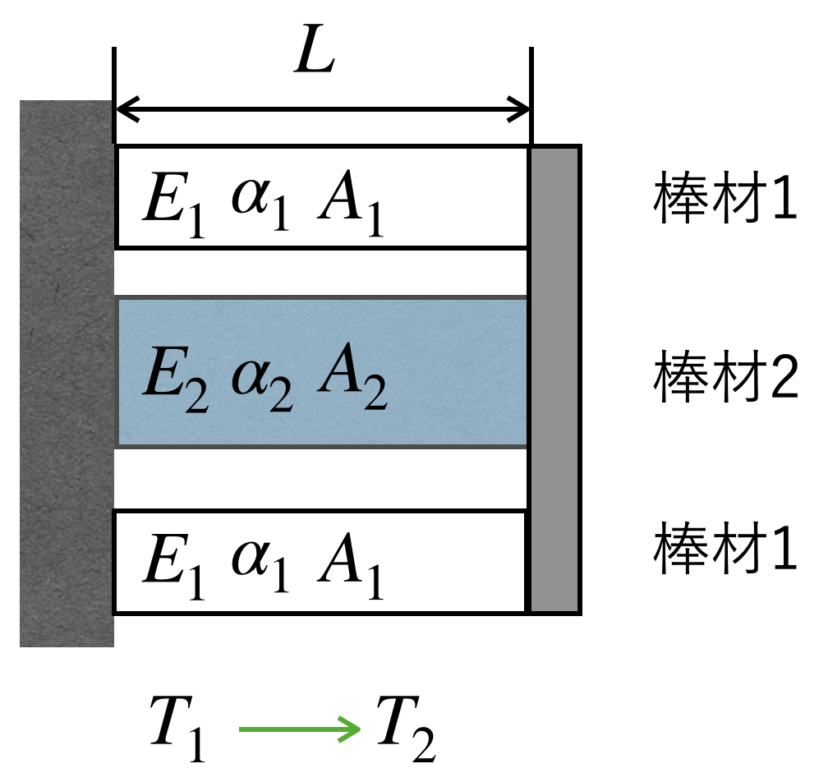
問1と違うところは、各棒材の右側は、「板」に固定されているということです。

そのため、膨張したときに棒材は多少は伸び縮みができます。しかし、棒材1と棒材2の線膨張係数が異なるため、変形量が制限されたり、引き延ばされたりします。

複雑そうには見えますが、最初に考えることは問1と同じく、熱と荷重とを分解して考えます。

温度がT₁からT₂になったときに、各棒材がΔLだけ伸びたとすると、各棒に働く現象は、以下の図のようになります。

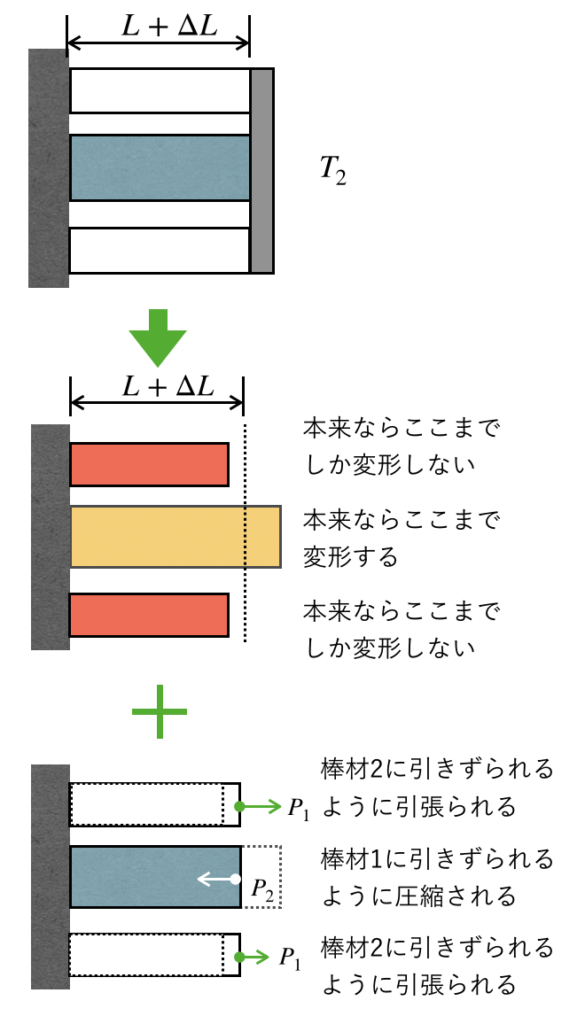
ここでは、棒材1に引張荷重が、棒材2に圧縮荷重がかかっているとしておりますが、実際にどちらの材料が圧縮荷重がかって、どちらの材料が引張荷重がかかっているかは、実際の物性値によりますので、上図の関係が逆でもOKです。

この図から、各棒材の伸びに着目すると、以下の関係式が得られます。

$$\begin{array}{rl}2{\epsilon }_1\mathrm{\Delta }L& ={\epsilon }_2\mathrm{\Delta }L\\ 2({\epsilon }_{t1}+{\epsilon }_{F1})& ={\epsilon }_{t2}+{\epsilon }_{F2}\\ 2({\alpha }_1(T_2-T_1)+\frac{{\sigma }_1}{E_1})& ={\alpha }_2(T_2-T_1)+\frac{{\sigma }_2}{E_2}\\ 2({\alpha }_1(T_2-T_1)+\frac{F_1}{A_1{E}_1})& ={\alpha }_2(T_2-T_1)+\frac{F_2}{A_2{E}_2}\cdots (1)\end{array}$$

ここで、各棒の右端に固定されている断熱板に着目すると、以下の式が得られます。

$$\begin{array}{r}2P_1-P_2=0\cdots (2)\end{array}$$

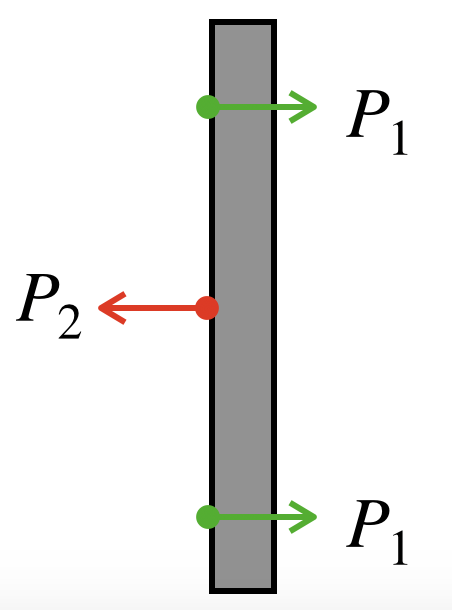
また、各棒を仮想的に切り離し、内力をF1、F2とすると

$$\begin{array}{r}{F}_1=P_1\cdots (3)\\ F_2=P_2\cdots (4)\end{array}$$

(1)に、(3)と(4)を代入すると、

$$\begin{array}{rl}2({\alpha }_1(T_2-T_1)+\frac{P_1}{A_1{E}_1})& ={\alpha }_2(T_2-T_1)+\frac{P_2}{A_2{E}_2}\cdots (5)\end{array}$$

(2)式と(5)式の連立方程式を解くと、

$$\begin{array}{r}\{\begin{array}{l}2P_1-P_2=0\\ 2({\alpha }_1(T_2-T_1)+\frac{P_1}{A_1{E}_1})={\alpha }_2(T_2-T_1)+\frac{P_2}{A_2{E}_2}\end{array}\end{array}$$

$$\begin{array}{r}{P}_1=\frac{({\alpha }_2-2{\alpha }_1)(T_2-T_1)A_1{A}_2{E}_1{E}_2}{2(A_2{E}_2-A_1{E}_1)}\\ P_2=\frac{({\alpha }_2-2{\alpha }_1)(T_2-T_1)A_1{A}_2{E}_1{E}_2}{A_2{E}_2-A_1{E}_1}\end{array}$$

よって、各棒材にかかる応力をσ₁、σ₂とすると、

$$\begin{array}{r}{\sigma }_1=\frac{({\alpha }_2-2{\alpha }_1)(T_2-T_1)A_2{E}_1{E}_2}{2(A_2{E}_2-A_1{E}_1)}\\ {\sigma }_2=\frac{({\alpha }_2-2{\alpha }_1)(T_2-T_1)A_1{E}_1{E}_2}{A_2{E}_2-A_1{E}_1}\end{array}$$

これが答えとなります。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...