演習問題 06【ねじり問題】

問題

問1

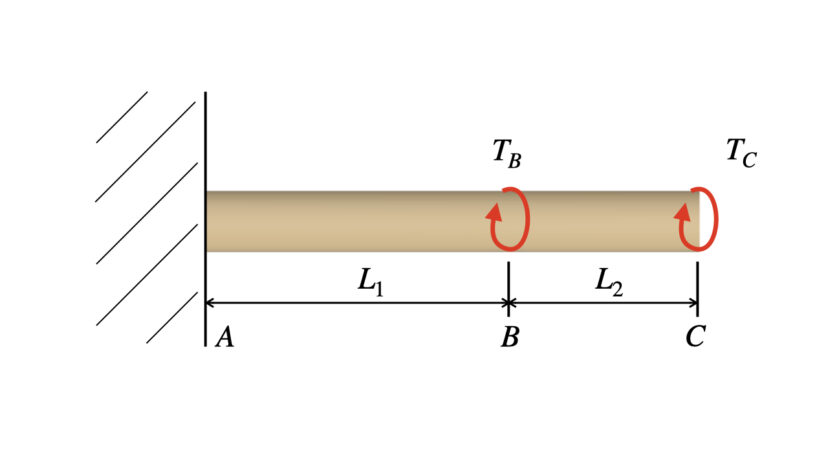
壁に固定された丸棒に、ねじり荷重を加えます。

このとき、丸棒に発生するねじり応力の最大値を求めてください。

ここで、T_B=3 N･m、T_C=4 N･m、L₁=300 mm、L₂=400 mmとします。

また丸棒はd=30 mmの中実軸とし、極断面係数は以下の式で計算できるとします。

$$Z_p=\frac{\pi d^3}{16}$$

答え

問2

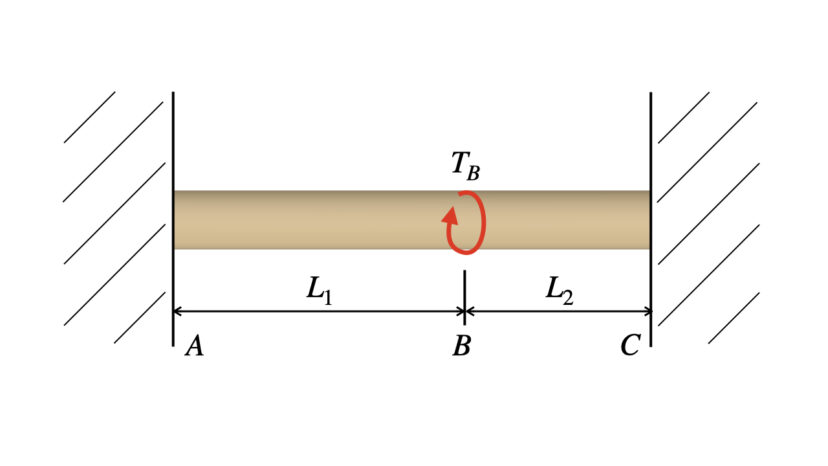
壁に固定された丸棒に、ねじり荷重を加えます。

このとき、A・Cに発生するねじり荷重T_A、T_Cを求めてください。

答え

答え

問1

ねじり荷重の問題に限らず、材料力学の問題を解く上での基本は、以下の3ステップです。

1. 荷重の釣り合いを考える。
2. 仮想的に切り離す。
3. 内力を求める。

まずは釣り合いの式を立てます。

壁に固定されておりますので、丸棒は壁から反力を受けます。壁から受ける反力をT_Aとしてモデルを書き直すと、下記のとおりとなります。

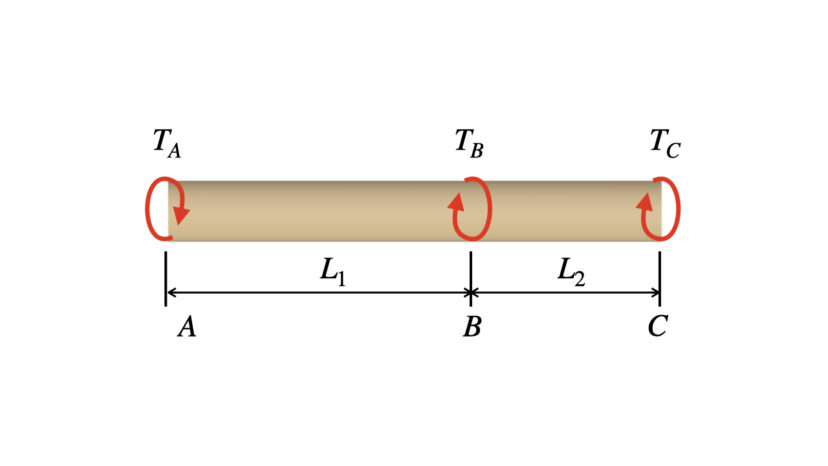
$$\begin{array}{rl}& T_A-T_B-T_C=0\\ & T_A=T_B+T_C\cdots (1-1)\end{array}$$

では続いて、丸棒を仮想的に切り離し、内力を求めていきます。

まずはAB間で仮想的に切り離し、方程式を立てます。

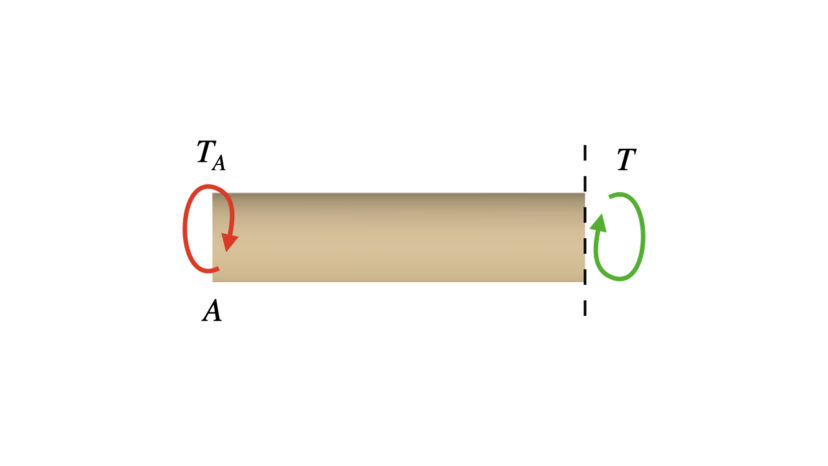
$$\begin{array}{rl}& T_A-T=0\\ & T=T_A=T_B+T_C\cdots (1-2)\end{array}$$

よって、AB間で発生するねじり応力の最大値は、

$$\begin{array}{rl}{\tau }_{AB}& =\frac{T}{Z_P}\\ & =\frac{16(T_B+T_C)}{\pi d^3}\cdots (1-3)\end{array}$$

続いて、BC間で仮想的に切り離して考えてみます。

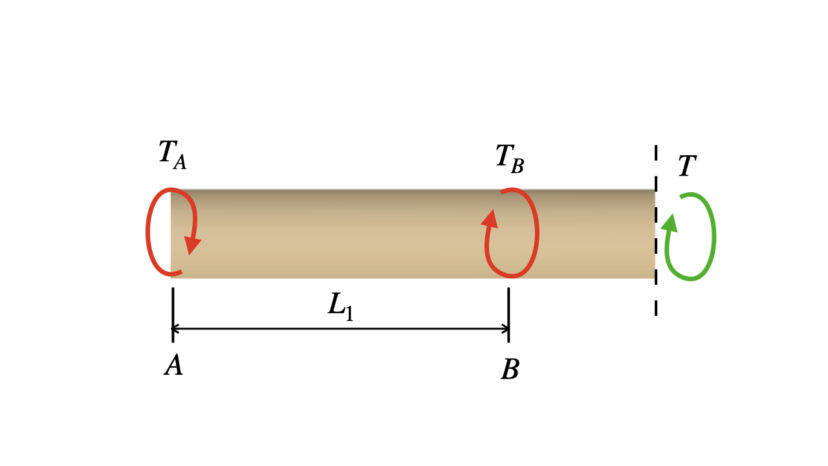
$$\begin{array}{rl}& T_A-T_B-T=0\\ T& =T_A-T_B\\ & =T_B+T_C-T_B\\ & =T_C\cdots (1-4)\end{array}$$

よって、BC間で発生するねじり応力の最大値は、

$$\begin{array}{rl}{\tau }_{BC}& =\frac{T}{Z_P}\\ & =\frac{16T_C}{\pi d^3}\cdots (1-5)\end{array}$$

ここで、(1-3)式と(1-5)式を比べてみますと、どの数値も正の値なので、区間ABで発生するτ_ABの方が値が大きいことがわかります。

そして、τ_ABの各文字部に、それぞれ値を代入して計算をします。

$$\begin{array}{rl}{\tau }_{AB}& =\frac{16(T_B+T_C)}{\pi d^3}\\ & =\frac{16(3Nm+4Nm)\times {10}^3}{\pi (30mm{)}^3}\\ & \simeq 1.32N/m{m}^2\end{array}$$

これが答えです。

問2

まずは基本に忠実に、釣り合いの式を立てていきます。

棒は壁から反力を受けるため、Aで受ける反力をT_A、Cで受ける反力をT_Cとすると、釣り合いの式は以下のとおりとなります。

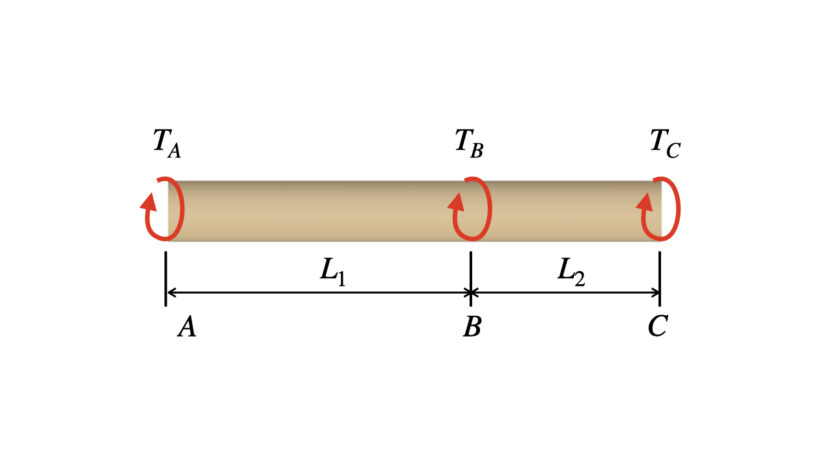
$$T_A+T_B+T_C=0\cdots (2-1)$$

しかし、(2-1)式には未知数(T_A、T_C)が2つに対して、式が1つしかなく、このままでは問題を解くことができません。

つまり、この問題は不静定問題です。

不静定問題はどのように解くか？

それは、変形量に着目をして、もう一つの式を立てます。

ねじり荷重の問題における変形量とは、ねじれ角φです。

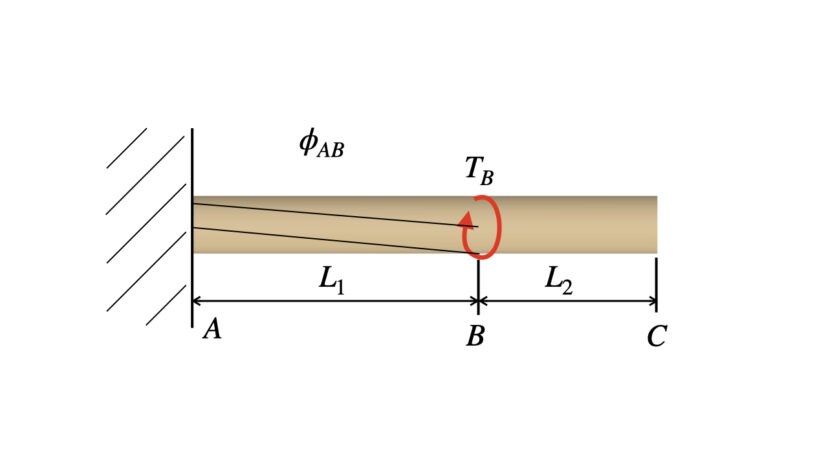
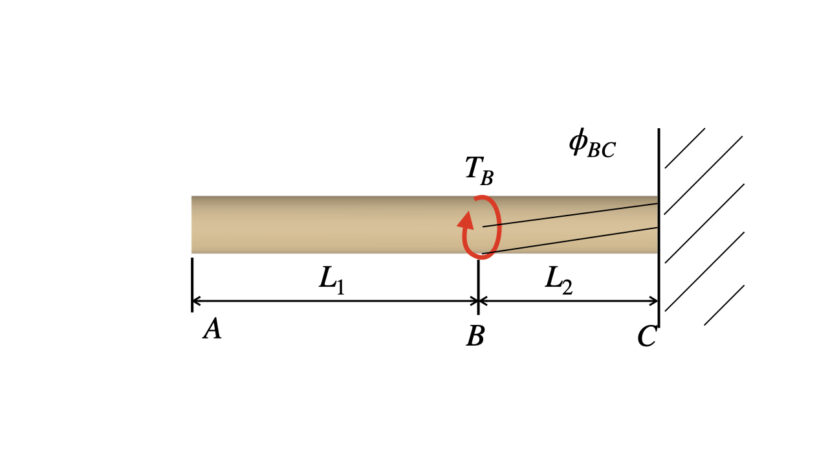
しかし、棒の両端が壁に拘束されていることから、以下の式が成り立ちます。

$${\varphi }_{AB}+{\varphi }_{BC}=0\cdots (2-2)$$

ここで、ねじれ角とひずみの関係を使うと、(2-2)式は以下のようになります。

$$\frac{L_1}{r}{\gamma }_{AB}+\frac{L_2}{r}{\gamma }_{BC}=0\cdots (2-3)$$

続いて、フックの法則を使うと(2-3)式は以下のようになります。

$$\begin{gathered} \frac{L_1}{{\tau }_{AB}G}+\frac{L_2}{{\tau }_{BC}G}=0 \\ \frac{L_1}{{\tau }_{AB}}+\frac{L_2}{{\tau }_{BC}}=0\cdots (2-4) \end{gathered}$$

そして、ねじり荷重とねじり応力との関係より、(2-4)式は以下のようになります。

$$\begin{gathered} \frac{L_1{Z}_p}{T_A}+\frac{L_2{Z}_p}{T_C}=0 \\ {\displaystyle \frac{L_1}{T_A}}+\frac{L_2}{T_C}=0\cdots (2-5) \end{gathered}$$

これで2つめの式ができました。よって、(2-1)式と(2-5)式を解くことで、答えを求めることができます。

$$\begin{array}{r}\{\begin{array}{l}{T}_A+T_B+T_C=0\cdots (2-1)\\ {\displaystyle \frac{L_1}{T_A}}+{\displaystyle \frac{L_2}{T_C}}=0\cdots (2-5)\end{array}\\ T_A=T_B\frac{L_1}{L_2-L_1}\\ T_C=-T_B\frac{L_2}{L_2-L_1}\end{array}$$

これが答えとなります。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...