ねじりの応力の導出を解説

前回、断面二次極モーメントを導入について解説をしました。

断面二次極モーメントの定義

今回はねじれ応力の導出についてお話しします。 前回、ねじれ荷重におけるひずみの話をしました。 ここで登場したのは、以下の2つの式です。 $$\gamma=r\theta\cdots(1)\\\tau=…

https://rivi-manufacturing.com/mechanics-of-materials/1679

そして、断面二次極モーメントを定義することによって、以下の関係式を得ることができました。

$$T=\frac{\tau_{max}}{a}I_p\cdots(1)$$

ここまでくれば、ねじりの応力の導出まであともう少しです。

では、ねじりの応力の求め方についてお話をしていきます。

せん断応力と、最大せん断応力の関係式の活用

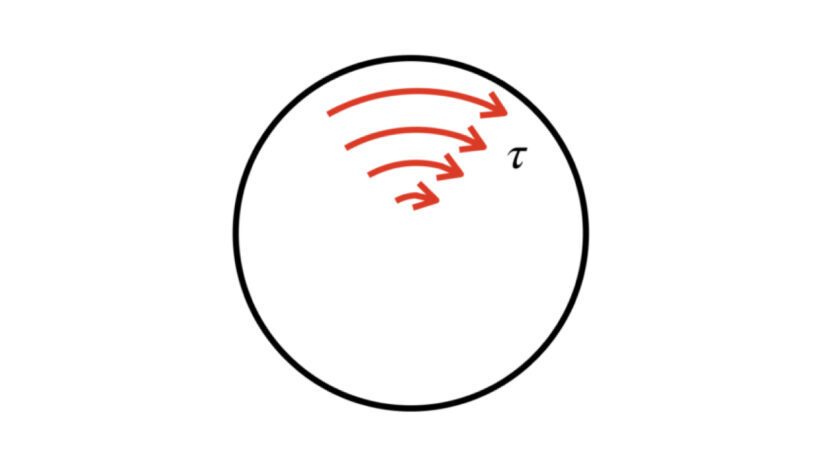
ところで、前回お話ししたように、せん断応力τと、せん断応力の最大値τ_maxの間には、以下の関係式があります。

$$\tau=\frac{r}{a}\tau_{max}\\
\frac{\tau_{max}}{a}=\frac{\tau}{r}\cdots(2)$$

よって、これを(1)式に代入すると、以下のようになります。

$$
T=\frac{\tau}{r}I_p\\
\tau=\frac{Tr}{I_p}\cdots(3)
$$

ちなみに、rが最大のとき、つまり、仮想断面の一番外側が最もねじりの応力が高いので、rは丸棒の半径が入ります。

極断面係数の導入

(3)式の、r/I_pの部分に着目してみますと、rもI_pも仮想断面の形状によって決まる値です。
なので、このr/I_pを一つの記号でまとめます。

すると、(3)式は以下のようになります。

$$\tau=\frac{T}{Z_p}$$

これが、ねじりの応力の計算式となります。

ここで、Z_pは極断面係数と呼ばれます。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...