この記事を読むべき人
こんにちは、りびぃです。
動きモノや軸ものを設計する時に必ず使うベアリングですが、ベアリングを選定する上では設計する上で重要なポイントが複数ありまして、
その中の一つ「ベアリングの寿命計算」も非常に重要な検討項目となります。
初心者の人は、
え?ベアリングって生き物でもないのに寿命なんてあるの?
と思うかもしれませんが、実はベアリングだけではなくあらゆる材料で寿命は存在します。
寿命は「材料の摩耗・劣化・破壊」のことを指していて、例えば「自転車や車のタイヤが摩耗してタイヤ溝がツルツル」になったり、「長年使っていた家電製品が突然動かなくなったり」なども寿命です。
もちろんベアリングも例ではなく、寿命を迎えたベアリングは軌道面が剥がれてしまうという現象がよく起こります。


実際にベアリングを回してみると、普通のベアリングは滑らかに回る一方で、寿命がきたベアリングを回すと「ゴリゴリ」と音がなります。ゴリゴリのベアリングを使っていると、当然機械の性能も低下しますね。
ということで、いざベアリングを選定しようと、設計者のみなさんは各ベアリングメーカを開いてみるのですが、
うわ、全く頭に入ってこないわ・・・(そっ閉じ)
となった人も多いのではないでしょうか?笑
というのも、ベアリングのカタログの中身は
なんていう光景が繰り広げられているからです。

ベアリングのカタログって、紙で見ると六法全書ぐらいの分厚さがあります笑
ただ、ベアリングについて一から丁寧に教えてくれるような職場なんて私は聞いたことがないので、ほとんどの設計者は自力でカタログにへばりついて学習するしかないのです。

マジで初心者に不親切ですからね笑
そこで今回は、ベアリングの寿命計算について、初心者にわかりやすく解説をしていきます。
難しい言い回しをなるべく押さえて、一つ一つ丁寧にわかりやすく解説していきますので、ぜひ最後まで読んでくだされば幸いです。
ベアリングの寿命計算について突っ込んだ内容を説明する前に、まずはベアリングの寿命計算には他の部品とは違う特徴があるということについて説明をしていきます。
今までちょっとでも機械を設計した人の中には、
材料や部品に「寿命」というものがあるのはわかったけど、そもそもなんでベアリングだけこんな色々と計算しているの?ここまできっちり寿命計算させられる部品ってベアリングぐらいじゃね?
って思ったかもしれません。

実は摩耗がしやすい部品はベアリング以外にもたくさんあるのですが、そういった部品に対して寿命計算することはなかなかないのです。
結論を言うと、ベアリングを部品交換する場合、メンテナンスコストが高くついてしまう傾向があるため、事前検討を十分にすることが重要となるのです。
よっぽど特殊なベアリングを使わない限りはベアリング単体はそこまで高価なものではないのですが、
問題は、ベアリングは機械の奥深くに組込まれる場合が多いということです。
ベアリングは軸とハウジングの架け橋となるように組込まれますが、「よし、ダメになったベアリングを交換しよう」としても、
なんてていう感じで、ほぼ全バラシになることが多くなります。
でもまぁ、絶対に壊れない部品なんて存在しないんだから、寿命で壊れたんだったらしょうがないじゃん?
まぁ設計者目線だとついついそうなってしまうかもしれませんが、お客さん(特に生産現場を受け持っている人たち)の目線に立つと、
というように、非常に困る事態であるのです。

例えば、火力発電で使われるガスタービンなんか、設備が止まると電力の供給がストップしますからね・・・。身近な例でも、例えば洗濯機が壊れて洗濯できなくなると困りますよね?
なので寿命計算をして、想定した期間でベアリングが問題なく使えるかを検討したり、事前にベアリングの交換時期を予測したりすることが大切なのです。
ではここからは、具体的にどのようにしてベアリングの寿命を計算するのかについて解説していきたいと思います。
ベアリングやリニアガイドの寿命を計算するときには、定格寿命と呼ばれる指標が用いられます。

ベアリングなどのカタログを読んでいると、このへんからこの辺から若干話が複雑になるので、丁寧に説明していきますね!
この定格寿命というのは、「ある一定の荷重がかかった状態でベアリングを回転させ続けたときに、何回転までならベアリングがもつか?」を表すものです。
これは、内輪回転・外輪回転のどちらのケースでもOKです。

資料によっては「回転数」と書かれていますが、これは「回転回数」のことであり、「回転速度(rpm)」のことではないので要注意です。でも普通は「回転数」て書いてあったらrpmを指すので、日本語がややこしいんですよね・・・
ただたとえ科学のちからを使っても「ちょうど53万回転まで!」などのように正確に寿命を当てることはできません。
そこで、定格寿命では「53万回転までもつ確率が90%」などのように確率を使って表現されます。
この確率の数字は一般的に90%が用いられ(「信頼度90%」という風に表現されます)、これを基本定格寿命と呼ぶのですが、
これは裏を返すと「10%の確率で壊れる」ということになることからL10という記号が用いられます。

より厳しい条件を求めるとなると95とか99.9%とかという値を設定することもあるのですが、それぞれL5やL0.1の記号が使われますね!
ではここからはこのL10について、もう少し考えていきましょう。
このL10は、例えば荷重F1ならば53万回転までもつ確率が90%といった感じになりますが、仮に荷重がF2になると80万回転ぐらいになったりというように、「荷重」と「回転回数」の組み合わせが無限にあります。
そのためそのままの状態では、設計でベアリングを選定するときの指標としては非常に扱いにくいのです。
使いやすい指標となるためには、
のいずれかであることが望ましいです。
更にはその表現方法が、どのベアリングメーカでも共通であると、より扱いやすくなります。

そうすることによって、わざわざ計算をしなくとも、単純に「AベアリングとBベアリングとを比べると、Aの方がいいね!」などのように比較しやすくなります。
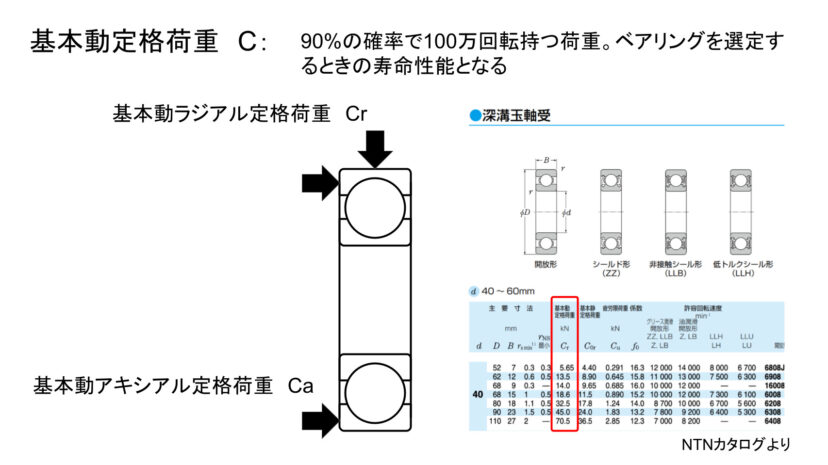
そこでJISでは、「回転回数の値を100万(106)回転と固定し、ベアリングが100万回転したときに、90%の確率でベアリングがもつ荷重は何kNか?」というふうにベアリングの寿命を表現することというふうに定められています。
このように「L10が100万回転となるような荷重」のことを「基本動定格荷重 C」と言います。
もう少し細かく述べると、ベアリングの荷重はラジアル(半径)方向と、アキシアル(軸)方向とに分けられますので、
カタログによっては「ラジアル基本動定格荷重 Cr」「アキシアル基本動定格荷重 Ca」などと分けて表記されていたりします。

100万という数字は、材料の疲労計算のところでもよく登場しますよね!100万回の繰返し荷重で破壊が起こるような荷重を疲労強度と呼び、設計ではよく「100万回もては十分だろ!」なんて判断することが多いです!
ここまで理解できるとベアリングのカタログがちょっと読めるようになってきますが、
うーん、なんだかよくわかんないや・・・
となる人も多いかと思います。

専門用語が続くと、頭がパンクしますよね笑
そんな人はとりあえず「基本動定格荷重 = ベアリングの寿命性能」と考えてもらえればOKです。
ここまででベアリングの寿命については富士山の8合目ぐらいまで来ているので、頂上までもうちょい頑張りましょー笑
では、ここまでの「基本定格寿命 L10」や「基本定格荷重 C」をどのように設計に活かせばいいのかについて説明します。
これら「基本定格〇〇」というのは、あくまで「xxだと仮定したときの〇〇」という指標ですから、
いやいや、ウチが設計している機械はそんな都合のいい条件で動かないんだけど・・・
って思いますよね。
なので、「設計する機械のベアリングが実際に受ける荷重がかかった状態で、90%の確率でもつ回転回数L10はいくつか?」を計算します。
計算式は以下の通りとなります。
$$L_{10}=(\frac{C}{P})^3\cdots(玉軸受の場合)$$
$$L_{10}=(\frac{C}{P})^{10/3}\cdots(ころ軸受の場合)$$
| $$L_{10}$$ | 定格寿命 [×106回転] |
| $$C$$ | 基本動定格荷重 [kN] |
| $$P$$ | 動等価荷重 [kN] |
「玉軸受」と「ころ軸受」とで使う計算式が変わるのですが、「ころ軸受の方が寿命が長くなる」というのは覚えておきましょう。
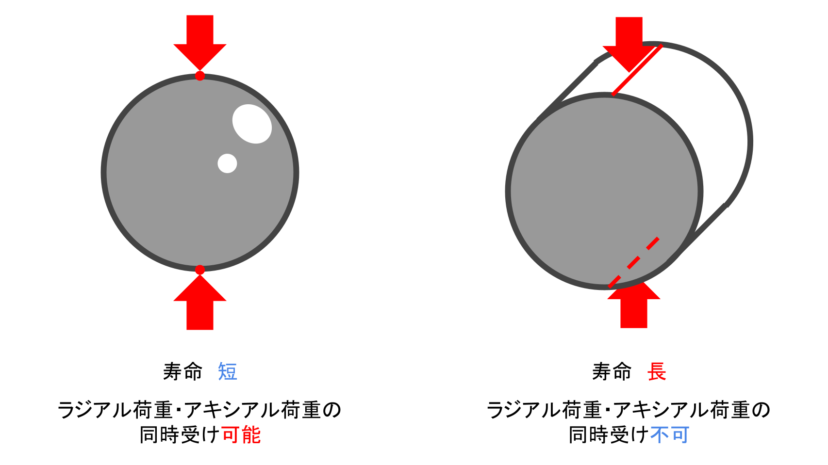
軸受にかかる荷重は玉やころももちろん受けることになるのですが、「玉は点接触で荷重を受ける」のに対して「ころは線接触で荷重を受ける」ので、応力が低くなるのです。

式中のn乗のところを見てみても、玉軸受は「3」に対して、ころ軸受は「10/3 = 3.33…」となっているので、ころ軸受の方が大きな値が得られるようになっていますね!
ただ、玉軸受には「ラジアル荷重・アキシアル荷重の同時受けが可能」という大きなメリットがあることから、玉軸受の方が使用頻度が高いです。
続いて数式の中身を見てみましょう。
まず、ここで初めて出てきた「動等価荷重」ですが、これは「実際のベアリングが受ける荷重に関する値」が代入されます。
実際に代入される値は、
を使って計算をし、求めていきます(具体的な計算方法はカタログをご参照ください)。
ただ、ここで押さえておきたいのは「式の意味」です。
右辺を見ると、基本動定格荷重と動等価荷重の比になっていることから、「100万回転してももつ確率が90%となる荷重(ベアリングの寿命性能を表現ときの基準)Cに対して、実際にベアリングが受ける荷重Pがどの程度の大きさか」を表しています。
ここで例えば、P=C、つまり実際のベアリングが受ける荷重が基本動定格荷重に等しいとすると、計算結果はL10=1となります。
ただし、L10の単位は×106回転ですから、L10=1は「100万回転」を意味することになります。

基本定格荷重のそもそもの定義は「100万回転で壊れる確率が90%となる荷重」でしたが、これで実際の計算でもそのとおりになっているということが明らかになったと思います。
最後にべき乗の部分が気になるところですが、これはおそらく「経験則」によって決められた数値だと思われます。
なので「そういうものなのだ」というふうに割り切ってしまってオッケーです。

摩耗などを扱った学問のことを「トライボロジー」といいます。ただベアリングだけに限らず「材料の摩耗についての高精度な計算・解析」は非常に難しいので、機械設計をする範囲であればこれ以上の深追いは不要です。どうしても詳細が気になる方は、日本トライボロジー学会 転がり軸受寿命研究会をご参照ください。
先程までで基本的な寿命計算の話題については終わりですが、最後の最後でちょっとした問題があります。
それは、L10の単位である「×106 回転」が直感的に分かりづらいのです。
例えば、家電製品の保証期間などでは「○年」などのように時間で表現されていますし、自動車の寿命だと走行距離を見て「あー、10万km超えたから、そろそろ寿命かなー」なんて判断することが多いです。

例えば、「L10=0.9でした!」と言われても「要するにいつまで使えそうなの?」ってなりますよね笑 時間や走行距離で表現したほうがみんなに馴染みがあります。
そのため、一般的な装置・機械については「時間」で、台車や自動車などは「走行距離」で寿命を表現してあげるのが親切です。
単位変換は以下の通りとなります。
【寿命時間】
$$L_{10h}=\frac{10^6}{60n}\left(\frac{C}{P}\right)^3=\frac{10^6}{60n}L_{10}\cdots(玉軸受)$$
$$L_{10h}=\frac{10^6}{60n}\left(\frac{C}{P}\right)^{10/3}=\frac{10^6}{60n}L_{10}\cdots(ころ軸受)$$
| $$L_{10h}$$ | 定格寿命 [hr] |
| $$n$$ | 回転速度 [rpm] |
【寿命走行時間】
$$L_{10s}=\pi D \left(\frac{C}{P}\right)^3=\pi D L_{10}\cdot(玉軸受)$$
$$L_{10s}=\pi D \left(\frac{C}{P}\right)^{10/3}=\pi D L_{10}\cdot(ころ軸受)$$
| $$L_{10s}$$ | 定格走行距離 [km] |
| $$D$$ | 車輪・タイヤの直径 [mm] |
以上、理論的にベアリングの寿命が計算できたわけですが、実はいくつかの注意点があります。
これをちゃんと押さえていないと、
え、壊れた!?いやいや、計算した寿命計算の結果とぜんぜん違うじゃん!ベアリングが不良品だったじゃね?
なんて考えにすぐなってしまう人が多いので、しっかり確認しましょう。
ベアリングの寿命計算では、以下の内容が計算の前提となっています。
もし、上記のような状況でベアリングを適応できない場合、まずはなにか設計の工夫で対策をするのが一般的となります。

例えば、「異物混入が問題になりそうなら、そもそも異物が入りにくいような構造にする」とかですね!
それも難しい場合は、L10にさらに補正係数を掛けて寿命計算をすることで、より確からしい寿命を見積ります。

このように補正係数を掛けて再計算した定格寿命のことを修正定格寿命と言ったりします(覚えなくても大丈夫です)。
具体的な計算方法は割と複雑なので、ここでは割愛します。
詳しくはJIS B 1518をご参照ください。
今回の記事は初心者向けにわかりやすいことを重視したので、実際に寿命計算をしていくためにはベアリングメーカーのカタログを読み解く必要があります。
ですが、この記事を読んだ上でカタログを開くと、内容がスラスラ頭に入ってくるようになっているかと思います。
なので特に、用語の意味についてはゆっくり本記事を読みながら理解を深めていただければ、有効的に活用できるかと思います。
なお、しぶちょー技術研究所というブログでも、初心者向けにわかりやすく解説していますので、合わせてご覧になるとより理解が深まるかと思います。
また、ベアリングは「寿命」以外にも着目するべき選定のポイントがいくつかあります。
ベアリング選定に関する全体感を掴みたいという方は、以下の記事が参考になりますので、よろしければご参照ください。
今回は以上となります。ご一読ありがとうございました。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

【解説】軸設計で検討するべき内容について