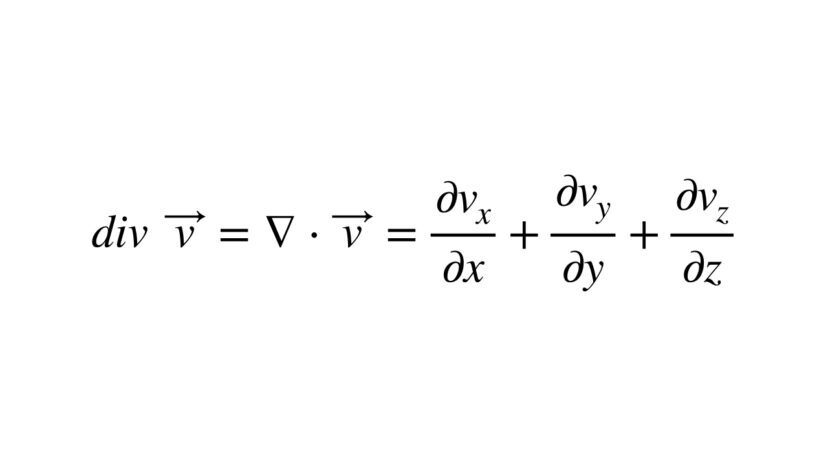
div(発散)の意味がよくわからない。一体、何の計算しているんだろ。流体の「湧き出し」とか「吸い込み」とかって聞くけれども、突然流体が湧き出したり、吸い込まれたりって、どういうこと?
このような疑問・悩みを持った人へお答えしていきます。
div(発散)というのは、ベクトル解析の勉強をしていくと登場する演算子(+とか×とかみたいな、計算の方法)の一種です。
ベクトル解析の勉強というと「数学者になる人だけが勉強するもの」という印象を持つ人もいるかと思いますが、流体力学や電磁気学などでもよく使用します。
発散は、例えば$$\vec{v}$$というベクトルに対して「発散」を計算するということを表したいときには、
$$div\ \vec{v}\ または\ \nabla\cdot\vec{v}$$
といったように表記をします(∇はナブラと読みます)。
そしてdiv(発散)定義を式で表すと、以下のようになります(xyzの3次元の場合)。
$$div\ \vec{v}=\nabla\cdot\vec{v}=\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}$$
ただ、この計算や計算式を見るだけでは「いまいちどんなイメージを持てばよいのか」「何のために計算をしているのか」が非常にわかりにくいと思います。
そこで今回は、このdiv(発散)の意味について、わかりやすくお話をしていきます。
発散は流体力学でもよく使用するということで、ここでは「流体」を使って解説をしていきたいと思います。
ここでいう流体は「空気」でも「水」でも、どちらでも構いません。
ここで、冒頭でもお話したように「発散」は「ベクトル」に対して使うものでした。
では、流体力学で登場する「ベクトル(大きさと方向の両方の概念を持つもの)」とは何かというと、代表的なのは「流体の速度(流速)」です。
そのため、流体が動いている様子、例えば「風が吹いている様子」とか「洗濯機を回している様子」とかをイメージすると良いです。
発散の話に行く前準備として、ここで「ベクトル場」を理解しましょう(発散は、ベクトルを扱うものですからね)。
ベクトルに「場」という単語がついておりますが、この「場」というのは「位置や時間の情報を入れることによって量(速度とか力とか)が取り出せるもの」です。
位置というのは「x,y,z」のこと、時間というのは「t」のことです。
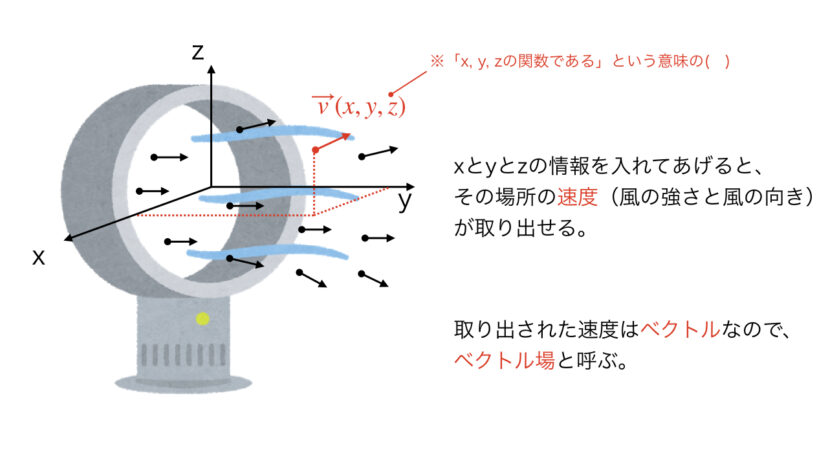
例えば、扇風機の周りを流れる空気の流速について考えてみましょう。
シンプルにするため、今回は「位置」だけを考え「時間」は無視します。
扇風機の周りの流速は、場所によって「風の強さ」や「風の向き」が異なります。
そのため「x座標」「y座標」「z座標」という位置情報をそれぞれ入れてあげると、その場所の「風の強さ」や「風の向き」を取り出すことができます。
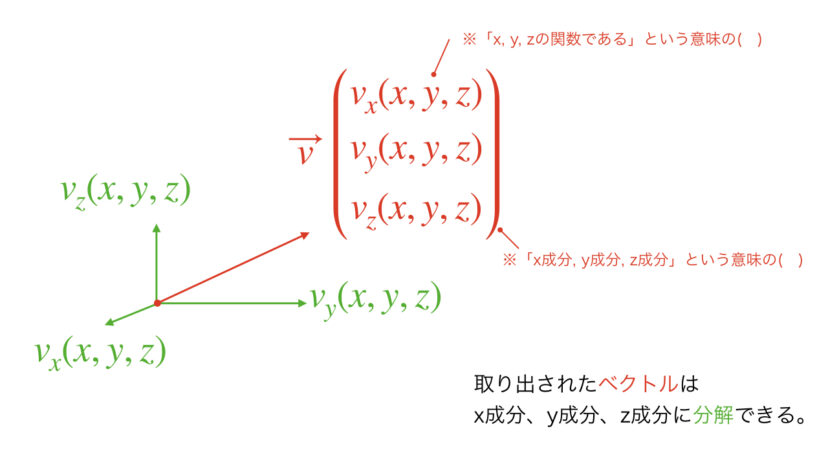
このようなものを「場」と言いますが、特に取り出される量はベクトルですので「ベクトル場」と呼ばれます。
ちなみに、取り出されたベクトルが速度の場合は「速度場」、応力の場合は「応力場」とか言ったりもします。
高校の数学などで習った「関数」は、取り出されるのがただの「値」でしたが、ベクトル場の場合は取り出されるのが「ベクトル」です。
そのため、取り出されたベクトルはx成分、y成分、z成分にそれぞれ分解することができます。
ここでは、取り出したベクトルの各成分を「vx」「vy」「vz」とすることとします。
このように分解できるというところが、高校数学で習うような関数と違うところであり、ベクトル場のわかりにくい部分の一つであると思われます。
「発散」とは何かというと、結論「単位体積あたりの(流出量)-(流入量)」のことを言います。
では、なぜ発散が「単位体積あたりの(流出量)-(流入量)」となるのか
これについて、式を導出しながら解説をしていきます。
まずは下の図のように、ベクトル場から取り出した流速vと、それを囲うように体積が「Δx × Δy × Δz」である直方体を置きます。(Δx、Δy、Δzは微小な長さとします)
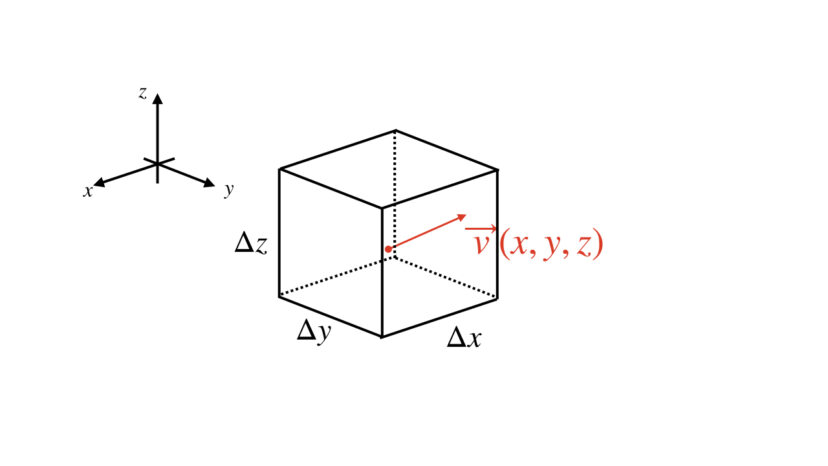
ここから、この直方体への流体の「流入量」と「流出量」を考えていきます。
最初はx軸方向のみに注目をして考えていきます
下の図で言うと、青の面から流入し、緑の面から流出していきます(流入面、流出面は逆でも構いませんが、ここでは青が流入、緑が流出とします)。
「流入量」や「流出量」を求めるためには、「流体の速度 [m/s] × 流体が出入りする面積 [m2]」で求められますが、x軸方向の「流体が出入りする面積」は、下の図から「Δy × Δz」だとわかるので、あとは「青の面」および「緑の面」から出入りする流速を求めていきます。
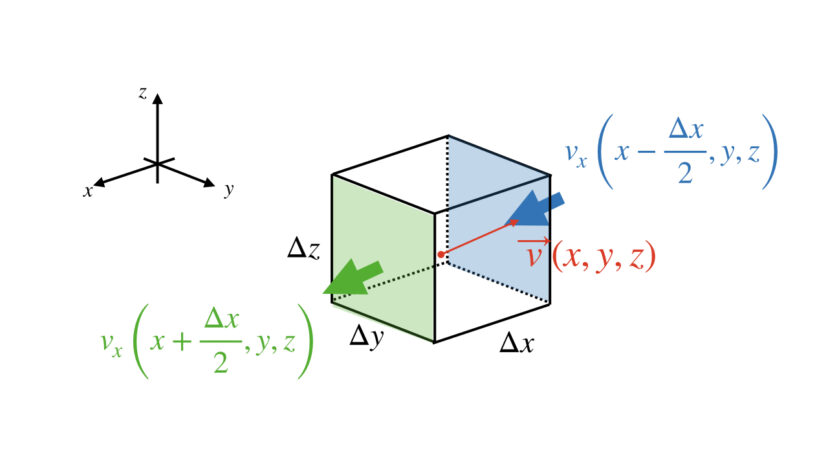
青の面から入る分の流速は以下のようになります。
$$v_x\left(x-\frac{\Delta x}{2},y,z\right)\ \left(※\vec{v}\left(x-\frac{\Delta x}{2},y,z\right)のうちのx成分\right)$$
青の面のy成分vy、z成分vzは、直方体への流入とは関係ないので無視します。
続いて、緑の面から出る分の流速は
$$v_x\left(x+\frac{\Delta x}{2},y,z\right)\ \left(※\vec{v}\left(x+\frac{\Delta x}{2},y,z\right)のうちのx成分\right)$$
緑の面のy成分vy、z成分vzは、直方体からの流出とは関係ないので無視します。
流量は「流体の速度 × 流体が出入りする面積」でしたので、x軸方向の「(流出量)-(流入量)」は以下のようになります。
$$\begin{align}&v_x\left(x+\frac{\Delta x}{2},y,z\right)\Delta y\Delta z-v_x\left(x-\frac{\Delta x}{2},y,z\right)\Delta y\Delta z\ \cdots(1)\end{align}$$
先ほど求めた(1)式ですが、このままでは扱いので「x=x」まわりでテイラー展開をします。
すると、(1)式は以下のように表すことができます。
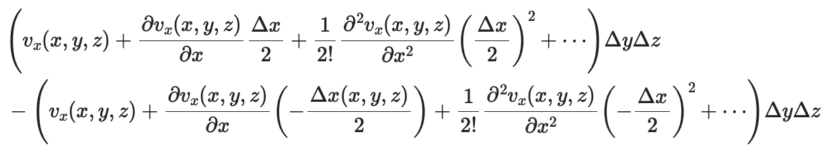
ここで、Δxが微小な長さであると仮定しているので、Δx2、Δx3・・・の項は「0」とみなします。
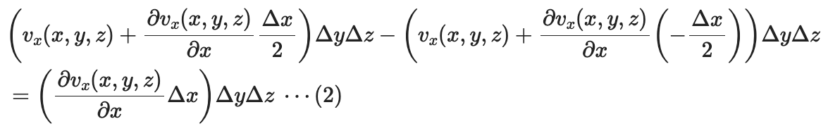
これでだいぶシンプルな形になりました。
ただ、多くの参考書等では「vx(x,y,z)」は「vxなどと省略して書かれますので、
$$\left(\frac{\partial v_x}{\partial x}\Delta x\right)\Delta y\Delta z$$
という表記になっていることがあります。
テイラー展開についてわからないという人は、こちらの記事をご覧ください。
x軸方向についての要領で、y軸方向、z軸方向の(流出量)-(流入量)について考えてみましょう。
詳しい解説は省きますが、結果は以下のようになります。
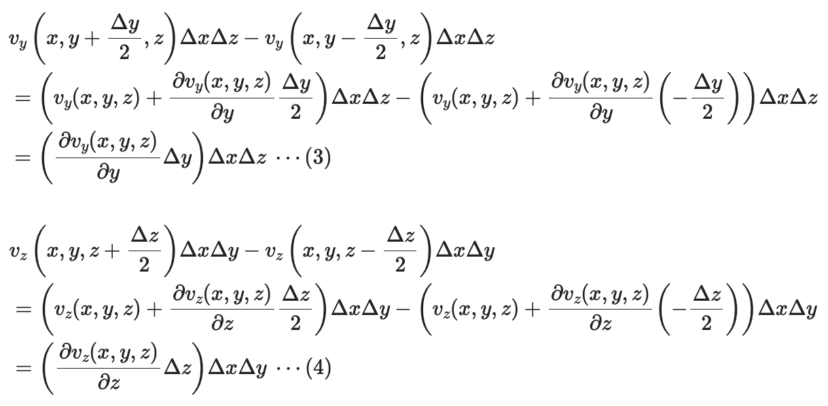
(2)と(3)と(4)を全て足し合わせると、体積が「Δx × Δy × Δz」である直方体への(流出量)-(流入量)を求めることができます。
$$\left(\frac{\partial v_x(x, y, z)}{\partial x}+\frac{\partial v_y(x, y, z)}{\partial y}+\frac{\partial v_z(x, y, z)}{\partial z}\right)\Delta x\Delta y \Delta z\ \cdots(5)$$
ここで「単位体積あたり」の(流出量)-(流入量)を求めるために、(5)式を体積で割ります。
$$\begin{align}&\left(\frac{\partial v_x(x, y, z)}{\partial x}+\frac{\partial v_y(x, y, z)}{\partial y}+\frac{\partial v_z(x, y, z)}{\partial z}\right)\Delta x\Delta y \Delta z\cdot\frac{1}{\Delta x\Delta y \Delta z}\\&=\frac{\partial v_x(x, y, z)}{\partial x}+\frac{\partial v_y(x, y, z)}{\partial y}+\frac{\partial v_z(x, y, z)}{\partial z}\\&=\nabla\cdot\vec{v}=div\ \vec{v}\end{align}$$
よって「発散」は「単位体積あたりの(流出量)-(流入量)」を表していると言うことができます。
発散が「(流出量)-(流入量)を表している」という説明だけでは「それを計算して何になるの?」と思うかもしれませんので、もう少し噛み砕いて説明します。
発散は何を表すのかをわかりやすく言うと「その流体はどこからやってきたのか?どこへ行ったのか?」ということになります。
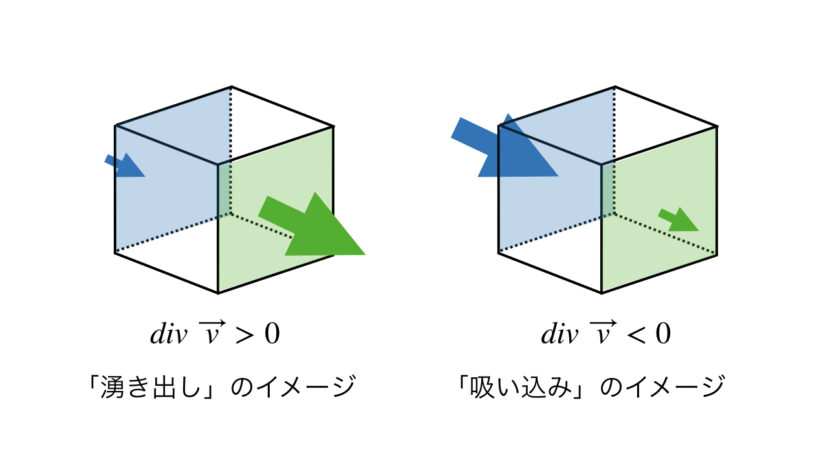
発散を計算した結果の符号についてまとめると以下の通りとなります。
発散が0の場合はイメージがしやすいかと思いますが、+やーの場合はイメージがしにくいかと思います。
これについて解説をしていきます。
まず発散が+の場合は、「流入した量以上が、流出してきた」ということになりますが、流入量+αの「+α」は一体どこからやってきたのかという疑問がわきます。
これは、「直方体の中から、湧き水のように流体が湧き出してきた」ということになります。
このことから、発散が+の場合は「湧き出し」と言われたりします。
一方で、発散がーの場合は、「流入した量未満しか、流出してこなかった」ということになりますが、流出してこなかった分は一体どこへ行ったのか?という疑問がわきます。
これは、「直方体の中へ、ブラックホールのように流体が吸い込まれていった」という意味になります。
このことから、発散がーの場合は「吸い込み」と言われたりします。
ですが冷静に考えてみると、「流体が別空間から現れたり、別空間へ出ていったりする状況」というのはありません。
流体の「湧き出し」や「吸い込み」というのはあくまでイメージの話であることを頭に入れていただき、実際のところは次のような状況で使われるということを覚えておいてください。
流体は収縮したり、膨張したりする性質があります。
多くのケースでは計算簡略化のため「流体は膨張も収縮もしないもの」として取り扱いますが、特定の条件下では「膨張や収縮」が生じるものとして取り扱います。
この性質のことを「圧縮性」といいます。
直方体の中へ流入した流体が、直方体の中で膨張や収縮が起こると、流体の体積が変化します。
そうすると、流入量と流出量とが釣り合わなくなります。
直方体の中で膨張したケースは「まるで流体が直方体の中から湧き出した」ようになるので発散が「+」の符号になります。
一方で、直方体の中で収縮した「まるで流体が直方体の中のどこかへ吸い込まれていった」ようになるので、発散が「ー」の符号になります。
流体の圧縮性についての詳しい解説はこちらをご覧ください。
多くの物質は、温まると膨張し、冷えると収縮するという性質があります。
そのため、直方体の中へ流入した流体が、直方体の中で温度変化すると、流体の体積が変化し、流出量と釣り合わなくなります。
直方体の中で膨張したケースは発散が「+」の符号に、直方体の中で収縮したケースが「ー」の符号になります。
今回のポイントについてまとめると、以下の通りとなります。
ベクトルの話は、なかなかとっつきにくい部分が多いので、今回の記事で知識を整理整頓していただければ幸いです。
今回の話は、大学時代に読んでいた下の教科書にも詳しく掲載されております。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


流体の圧縮性・非圧縮性【紙くずとダイヤモンドというイメージです】