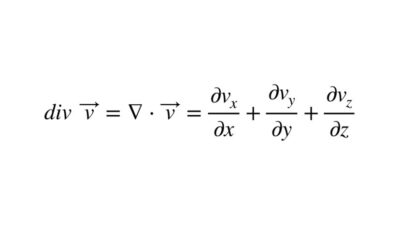
流体力学を勉強していて、「非圧縮」だとか「圧縮」だとかってよく耳にするけれども、なんかイメージできない。色んな分類が出てきて混乱するし、そもそもそういうふうに分類して何の役に立つの?
このような疑問・悩みを持った人へお答えしていきます。
「圧縮性・非圧縮性」というのは、「流体力学」という学問で登場する、流体の性質を表す用語です。
「流体力学」は流体の流れについて学ぶ学問で、機械系を専攻する学生にとっては、必須科目の一つになっているほど重要な学問です。流体は、空気や水蒸気などの「気体」と、水や油などの「液体」とを含み、これらの速度や圧力といった流れの挙動を計算・解析をしたりします。流体の流れに関する知識は、大学の研究などに使われたりしますが、最近では「水の流れをリアルに再現した映像の製作」などにも活用されています。
この「非圧縮性」を前提とした方程式や式展開は授業でたくさん出てくるのですが、大学の授業を一回聞くだけでは一体何のことを言っているのかがよくわからないという人も多いのでしょうか。
事実、私は慶應義塾大学の理工学部を卒業しているのですが、「流体力学」の単位を落とす学生は毎年ある程度の割合おり、さらに私はその中の一人でした。
みなさんには私のような苦い思い出をしてほしくないので、今回は流体の「圧縮性・非圧縮性」についてわかりやすく解説したいと思います。
目次
圧縮性を一言でいうと「縮んだり、膨らんだりする」、非圧縮性を一言で言うと「縮んだり、膨らんだりしない」という意味になります。
これは、紙くずをイメージしてもらうとわかりやすいです。
紙くずを「ぐしゃっ」と潰すと紙くずは縮みますし、紙くずを少しほぐしてあげると紙くずは膨らみますよね。
これは紙くずはもちろん、空気や水でも同様のことが起こり、これが「圧縮性」です。
一方で、「非圧縮性」とはダイヤモンドのようなイメージです。
ダイヤモンドは力を加えても縮んだり、膨らんだりはしませんよね。
そんなイメージを持っていただければよいです。

厳密に言いますと、世の中の全ての流体は「圧縮性」です。
流体によって、ちょっとの力で縮んでしまう流体とか、かなりの力をかけないと縮まない流体とかという程度の違いはあるのですが、「力をかければ縮む、圧縮する」という現象そのものは共通です。
この「圧縮性」に関してキーワードになるのが「密度」です。
密度というのは、単位体積あたりの重量のことを言い、「g/cm3」とか「kg/m3」という単位で表します。
なぜ「密度」がキーワードになるかというと、「圧縮するということは、密度が変化する」ということだからです。
この密度が変化するということについて、もう少し詳しくお話していきます。
密度を計算するには、「g/cm3」という単位から見てもわかるとおり、「重量を体積で割る」ことで計算できます。
このことから、「密度が変化する」ということは、次の3つのうちのいずれかが発生しているということになります。
このうち、流体が圧縮するときに発生するのは2番目の内容です。
さきほどの紙くずの例を思い出してほしいのですが、紙くずをグシャグシャに丸めたとしても、紙くずが重くなることはありません。
ただし、紙くずをグシャグシャにしたことによって、紙くずは縮みます。
つまり、紙くずのような流体を圧縮をすると、「重量÷体積」のうち「体積」の値が小さくなるので、密度は大きくなるのです。
先ほど、世の中の全ての流体は「圧縮性」だという話をしましたが、実は流体力学において特殊なケースを除き、ほとんどで流体を「非圧縮性」とみなします。
なぜ「流体は圧縮性をもつ」という真理に反して、ダイヤモンドのように縮みも膨らみもしない「非圧縮性」とみなすのか。
それは、「非圧縮性」とみなすことによって、大きなメリットを得ることができるからです。
「非圧縮性とみなす」とどんないいことがあるのかというと、「計算が簡単になる」のです。
流体力学ってめちゃくちゃ複雑で、厳密に計算や解析をしようとすると、高性能のコンピュータを使っても、数日〜数週間かかってしまうレベルです。
そのため、計算が簡略化できる、つまり「簡略化しても現実に則した現象を知る事ができる」というのは、めちゃくちゃメリットが大きいのです。
ここで、そもそも人間やコンピュータにとっても「計算が簡単」とはどんな計算なのかという説明をすると、それは以下の2つのような式のことを言います
例えば、「〇〇の項を無視する」「項を打ち消す」「計算すると0になることを証明する」などの方法によって、式そのものがシンプルになれば計算が簡単になりますし、
xyz軸の3次元計算よりも、xy軸の2次元計算、さらにx軸の1次元計算の方が計算は簡単です。
流体を「非圧縮性とみなす」と、この2つのことを実現することができるから、計算が簡単になるのです。
流体力学の中で手てくる最も大切の方程式の一つである「ナビエ・ストークス方程式」という式を見ていきましょう。
ナビエ・ストークス方程式の内容は、以下のとおりです。
$$\rho\left(\frac{\partial \vec{v}}{\partial t}+(\vec{v}\cdot\nabla)\vec{v}\right)=-\nabla p+\nu\nabla^2\vec{v}+\vec{f}+\frac{mu}{3}\nabla(\nabla\cdot\vec{v})$$
ここでは密度を記号ρで表していますが、圧縮性の場合は密度が変化するので、ρが変数となります。
ここで「非圧縮性」とみなすことによってこの方程式は以下のようになります。
$$\rho\left(\frac{\partial \vec{v}}{\partial t}+(\vec{v}\cdot\nabla)\vec{v}\right)=-\nabla p+\mu\nabla^2\vec{v}+\rho\vec{f}$$
項が1つ減ってシンプルになってのはもちろんですが、非圧縮性のナビエ・ストークス方程式の場合、密度は変化しないので「定数」として取り扱うことができます。
いくら計算が簡単になるからと言って、ほんとに「非圧縮性」という「真理に反した仮定」をしてしまってもいいのか、と疑問に持たれる人もいるかと思います。
実はご察しの通り、何でもかんでも非圧縮性とみなすことはできません。
非圧縮性とみなすための条件は、以下の2つです。
一つ目の温度変化の影響ですが、物体は一般的に「温度が上がると膨張する(熱膨張)」という性質があります。
「温度が上がれば、紙くずが膨らむように密度が減少する」という現象そのものはあるのですが、それもほんのわずかであれば「ダイヤモンドのように非圧縮性」とみなしても問題ないということです。
ここで、式を使って考えてみましょう。
ここで流体が気体の場合について考えてみます。
気体でかつ、温度変化とか密度とかの議論をする際には、高校物理の熱の分野ででてきた「気体の状態方程式」を使うと便利です。
$$pM=\rho RT$$
pは圧力、Mは分子量、ρは密度、Rは気体定数、Tは温度です。
この式を、以下のように変形してみます。
$$\frac{p}{\rho }=\frac{RT}{M}$$
ここで、流体に化学反応が起こったりすることがなく、Mを一定だとすると、温度の変化というは、結局のところ、圧力や密度を変化させるということがわかります。
続いて二つ目の圧力変化の影響は、冒頭の紙くずの例でいうと「紙くずがグシャグシャになったとしても、密度がほとんど変化していないとみなせる程度」ということです。
「紙くずのように流体は圧縮される」という現象そのものがあったとしても、それがほんのわずかであれば「ダイヤモンドのように非圧縮性」とみなしても問題ないということです。
ここで登場するのが、「マッハ数」という値です。
マッハ数の定義を式で表すと、以下の通りとなります。
$$Ma=\frac{v}{a}$$
ここで、Maはマッハ数、vは流体の速度、aは音速を表します。
マッハ数の意味は式を見てもわかるように「音速に対する速度」ですが、別の見方として「流体の弾性力(圧縮のしにくさ)に対する慣性力(圧縮する力)の比」としても見ることができます。
このマッハ数に対して、どうなっていれば「非圧縮性」とみなせるのかという説明をします。
これには、おおよその数値が決まっており、「マッハ数が0.3以下の場合」つまり「流体の速度が音速の0.3倍を以下の領域を扱う場合」では、非圧縮性とみなすことができます。
この0.3という値は、密度変化の影響が5%未満とみなせるということから由来しております。
非圧縮性とみなすことで、確かに計算誤差が生じるのですが、その影響が小さければ別に構わないということになるのです。
ちなみに、流体の圧縮・非圧縮に重要な「音速」ですが、状況によって値が異なることに注意してください。
例えば「気温15℃の空気中を伝わる場合は」は「音速340m/s」というのはよく聞きますが、
「気温15℃の水中を伝わる場合」となると「音速1,466m/s」にまで跳ね上がります。
このことから、「流体が何であるか」によって、非圧縮性・圧縮性の判断に使われる速度が異なるのです。
もちろん、空気の方が低い速度(100m/s強)で圧縮性とみなすことになり、逆に水の場合は99.9%ぐらいのケースで非圧縮性です。
今回のポイントについてまとめると、以下の通りとなります。
今回の話について、より詳細に知りたいという人は、こちらの書籍が参考になるかと思います。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

div(発散)の意味【流体の流れでイメージするといいです】