材料力学で出てくる熱応力の問題って、教科書だと内容が薄いのに、実際に解こうとすると難しくてうまく解けない。わかりやすく解説してほしい。
このような疑問・悩みを持った人へ、お答えしていきます。
結論から言うと、熱応力の問題は「ひずみから考える」のがポイントとなります。
大学で習う4力(機械・流体・熱・材料)の中で、最も仕事で使うのは材料力学で、この材料力学の知識なくして設計をすることはできません。
機械の設計として最も取り扱いが多いのは、金属材料ではありますが、ちょっとしたところに樹脂材料を使ったりもします。
そういったときに問題になりやすいのが、この熱応力です。
金属と樹脂とを組み合わせた装置では熱応力の知識がないと、部品が曲がったり、割れたりするなどの不具合が生じ、設計ミスへ繋がります。
ですがこの熱応力の問題は、教科書や参考書を見ると、かなり内容が薄いにも関わらず、実際に計算をしようとすると意外と解くのが難しかったりします。
大学の授業でも、熱応力の問題を苦手とする人は割と多いです。
今回はそんな熱応力に関する話の中から、実際の設計でもよく登場する「接合された2つの平板に発生する熱応力」についてお話をしていきます。
材料は、温度が上がると膨張し、温度が下がると収縮します。この材料の変形が、材料の拘束などによって妨げられると、それに相応する応力が材料に発生します。
この応力のことを熱応力と呼びます。
特に実際のものづくりにおいても、熱応力が問題となるのは、以下のようなケースです。
2つの平板間に働く熱応力の計算では、いきなり応力について考えるのではなく、まずはひずみから考えていきます。
そしてこのひずみは、「熱ひずみ」と「拘束によるひずみ」とに分けて考えるのがポイントです。
ここで例題を紹介します。
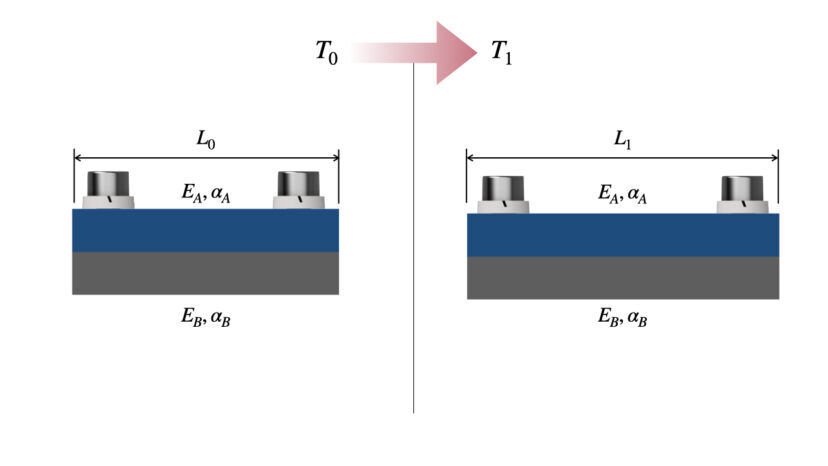
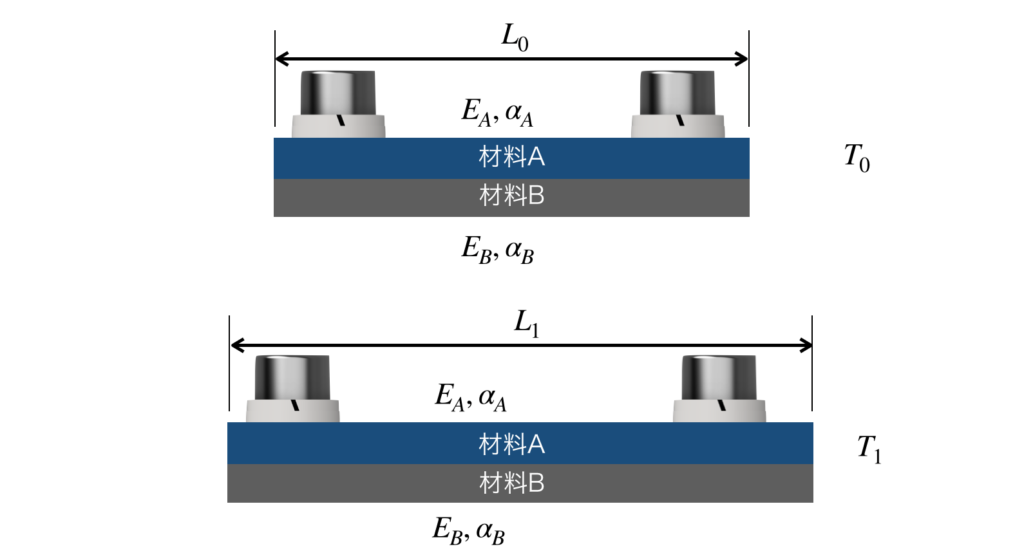
下の図のように、板の断面積SA、ヤング率EA、線膨張係数αAである材料Aと、板の断面積SBヤング率EB、線膨張係数αBである材料Bとを、温度T0の環境においてボルトで接合します。このとき、2つの材料の長さはL0とし、2つの材料の間に応力は発生していないものとします。
この状態から温度T1まで加熱をしたときの、熱応力について求めていきます。
まずは、2つの平板が接合されていなかったら、どうなっていたかについて考えます。
温度T1の時の、材料1の長さをL1A、材料2の長さをL1Bとします。仮に線膨張係数の値が、材料Aの方が大きいとすると、ぞれぞれの材料は膨張によって、以下の図のようになります(逆でも構いません)。
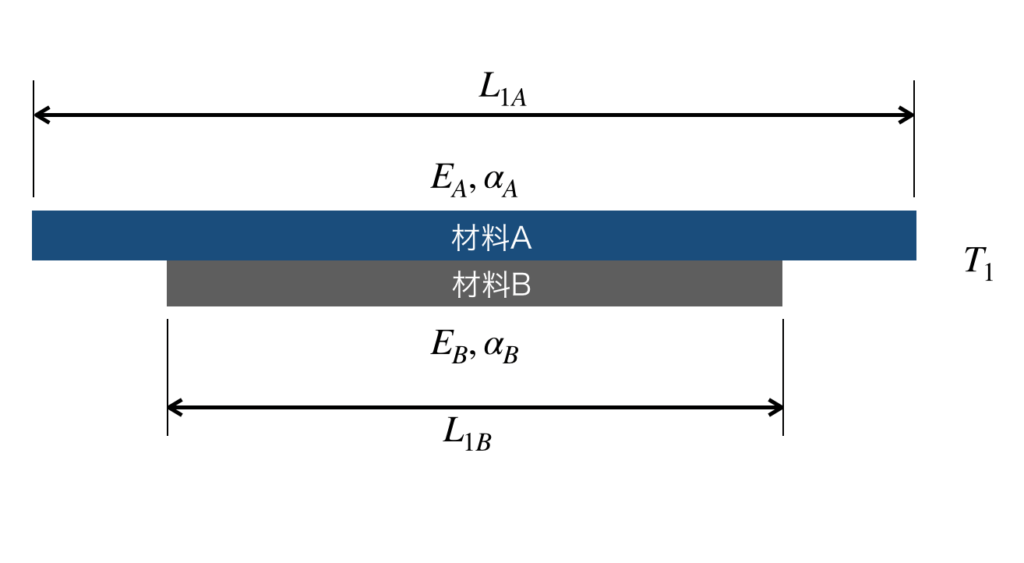
このように、材料の温度変化によって発生するひずみのことを、熱ひずみと呼び、以下のような式で表されます。
$$\begin{align}
\varepsilon_T=\alpha\Delta T
\end{align}$$
| $$\varepsilon_T$$ | :熱ひずみ |
| $$\alpha$$ | :線膨張係数 |
| $$\Delta T$$ | :温度変化 |
よって、材料A・材料Bそれぞれに発生する熱ひずみの大きさは、以下のように表されます。
$$\begin{cases}
\varepsilon_{TA}=\alpha_A(T_1-T_0)\cdots(1)\\
\varepsilon_{TB}=\alpha_B(T_1-T_0)\cdots(2)
\end{cases}$$
続いては、ボルト接合によって材料が受ける拘束について考えていきます。
しかし実際には、2つの平板はボルトで接合されているので、変形が妨げられます。
材料Aにとっては、本来ならばL1Aまで膨張できたのですが、材料Bに引きずられていることで、長さL1まで縮められています。
逆に材料Bにとっては、本来ならばL1Bまでしか膨張しないのですが、材料Aに引きずられていることで、長さL1まで伸ばされてしまっています。
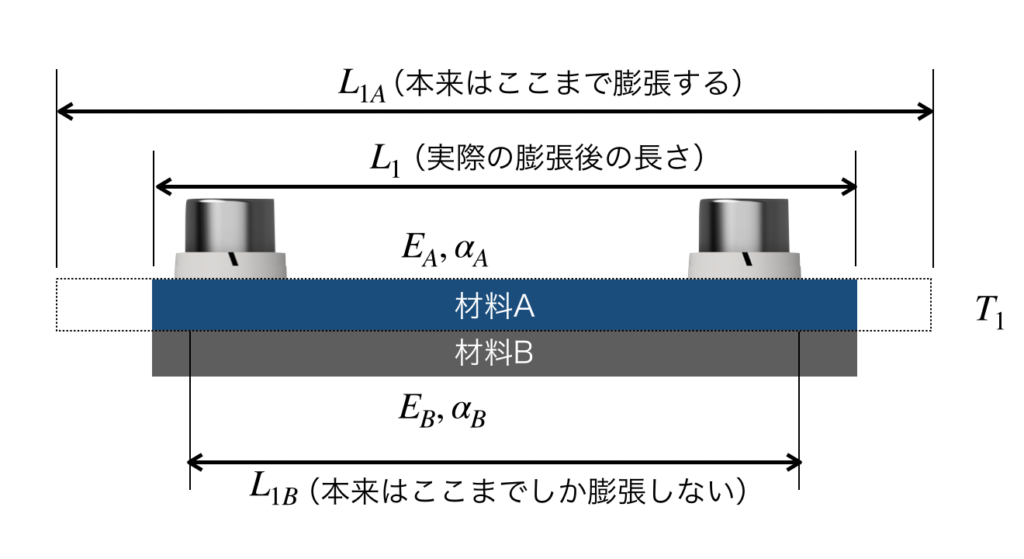
実はこの現象は、以下のように言い換えることができます(ここでいう〇〇荷重を、見かけの力と言うこととします)。
これを式で表すと、以下のとおりとなります。
$$\begin{align}
\varepsilon_{PA}=\frac{\sigma_A}{E_A}\cdots(3)\\
\varepsilon_{PB}=\frac{\sigma_B}{E_B}\cdots(4)
\end{align}$$
| $$\varepsilon_P$$ | :見かけの力によるひずみ |
| $$\sigma$$ | :材料が受ける応力 |
材料A・材料Bそれぞれについて、「熱ひずみ」および「見かけの力によるひずみ」が発生するのですが、最終的な変形量はL1となり等しくなるという条件を使います。
「ひずみ」に「変形前の寸法」を掛け算すると、変形量が求められることを利用すると、変形量は以下のように表すことができます。
$$(\varepsilon_{TA}+\varepsilon_{PA})\cdot L_{0}=(\varepsilon_{TB}+\varepsilon_{PB})\cdot L_{0}\\
\alpha_A(T_1-T_0)+\frac{\sigma_A}{E_A}=\alpha_B(T_1-T_0)+\frac{\sigma_B}{E_B}\cdots(5)$$
ただし、(5)式は、未知数が2つ(σA、σB)に対して、式が1つしかないため、式を解くためにはもう一つ関係式が必要となります。
もう一つの関係式が必要であるため、ここで材料が受ける力の釣り合いから式を立てていきます。
接合された2種類の材料が膨張するときに、それぞれの材料が受ける見かけの力をPA、PBとします。
すると、力の釣り合いより以下の関係式が成り立ちます。
$$-P_A+P_B=0\cdots(6)$$
また応力の定義より、(5)式は以下のように書き換えることができます。
$$\alpha_A(T_1-T_0)-\frac{P_A}{S_AE_A}=\alpha_B(T_1-T_0)+\frac{P_B}{S_BE_B}\cdots(7)$$
(6)式、(7)式を解くことによって、PA、PBは以下のようになります。
$$P_A=P_B=\frac{S_AS_BE_AE_B}{S_AE_A+S_BE_B}(\alpha_A-\alpha_B)(T_1-T_0)\cdots(8)$$
よって、各材料に発生する応力は、各材料の断面積で割って以下のように求められます。
$$\begin{align}
\sigma_A=\frac{S_BE_AE_B}{S_AE_A+S_BE_B}(\alpha_A-\alpha_B)(T_1-T_0)\\
\sigma_B=\frac{S_AE_AE_B}{S_AE_A+S_BE_B}(\alpha_A-\alpha_B)(T_1-T_0)
\end{align}$$
大学の材料力学において、多くの人が問題を解くことができないのが、この熱応力の問題です。
なぜ、解くことができないかというと、式の丸暗記だけでは解けないことが多いからです。
教科書によく載っている熱応力の計算式は、以下のとおりです。
$$\begin{align}
\sigma_T=E\alpha\Delta T\cdots(1)
\end{align}$$
| $$\sigma_T$$ | :熱応力 |
| $$E$$ | :ヤング率 |
| $$\alpha T$$ | :線膨張係数 |
| $$\Delta T$$ | :温度変化 |
しかし、この式の考え方等を初めから理解できる人は、なかなか少ないです。
以下の内容は、よく勘違いされやすいポイントです。
材料は温度が変化すれば、膨張・収縮を起こしますが、だからと言って必ず熱応力が発生するわけではありません。
熱応力が発生する条件は「膨張・収縮が妨げられたとき」です。
例えば下のように、長さがL0の材料の左端を壁に固定し、そこから材料の温度がT0からT1になるように熱を加えたとしましょう。

熱を加えられた材料は膨張するため、長さがL0からL1へ変化しますが、膨張自体が妨げられているわけではないので、熱応力は発生しません。
教科書に載っている(1)式が使えるのは、割と限定的です。
そのため、拘束される条件が異なれば、(1)式はそのまま使うことができません。
(1)式が使えるのは、材料と断熱壁との間に隙間がなく、材料の両端が断熱壁に挟まれているような状況です。
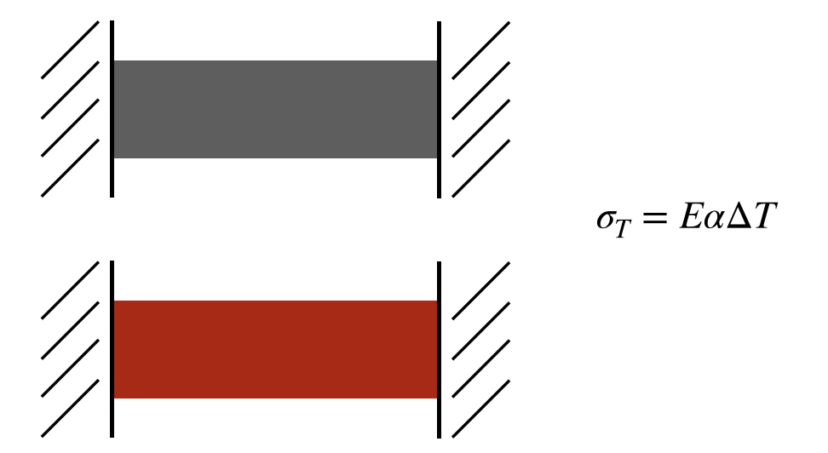
このように見なせない場合は、ひずみから熱応力を計算していくことになります。
今回のポイントをまとめると、以下のとおりとなります。
今回の記事が、熱応力の問題の克服に役立てていただければ嬉しいです。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

遠心力を受ける物体の伸びの計算方法【材料力学】
【解説】ヘルツの接触応力 | 公式集