応力ひずみ線図の読み方のポイント

材料力学の本質である
「どの程度変形するか」「どの程度の力で壊れるのか」
という性質をグラフで表したのが「応力-ひずみ線図」です。

材料力学の本質：応力とひずみの関係

材料は荷重を受けると、材料に応力が発生し、さらにひずみが発生します。つまり、「応力」と「ひずみ」には関係性があります。 これらの関係についてグラフで表したものを、応力-ひずみ線図と呼びます。 応力-ひ…

ものづくりのススメ

この応力-ひずみ線図ですが、材料力学の本質を表しているだけあって、様々な情報が表されております。

これは、中学校の数学で習う、比例・反比例のような、
「x=〇〇であるとき、y=△△となる」
という単純な情報だけではありません。

では、
応力-ひずみ線図にはどのような情報が載っているのか？
このグラフをどのように解釈したら良いのか？
について、今回はお話しします。

材料の硬さ

中学の比例・反比例的な読み方をすると、
ひずみがxのときに、材料にはyの応力が発生するという読み方ができます。
逆に、材料にyの応力が発生している時、材料はxひずむという読み方もできます。

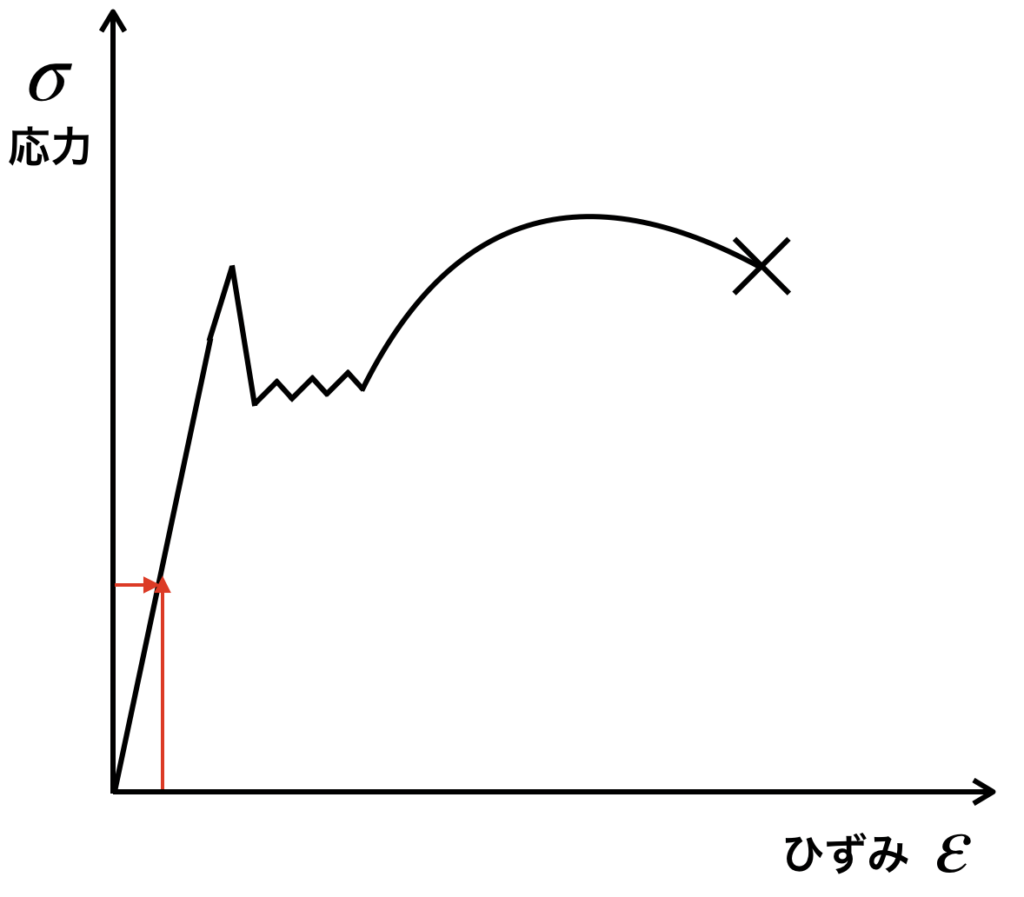
そして、グラフの傾きが大きい（ヤング率が高い）ほど、
材料はひずみにくい、つまり材料が硬いことを意味します。

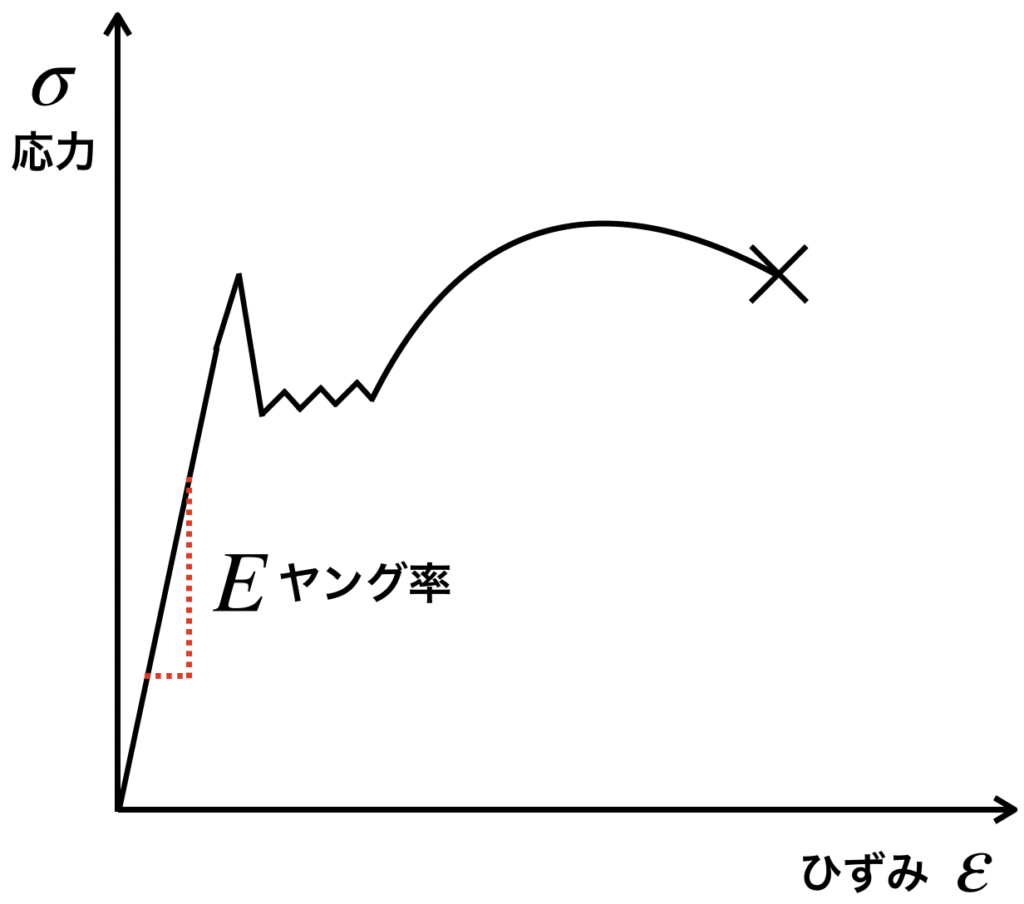
さらに、
ひずみがxの状態から、さらにx+x’の状態までひずませるために、
線図が右肩上がりであれば今より大きい応力が必要で、
右肩下がりであれば今より小さい応力しか必要がないという風に読めます。

ただ実際には、右肩下がりの場合は、どんどんひずみが進行することを意味するので、
右肩下がりの途中でひずみがキープされることはありません。

永久ひずみ（残留ひずみ）の量

応力-ひずみ線図の弾性限界を超えると、材料は塑性変形し、荷重を0にしても元の形状には戻らない永久ひずみ（残留ひずみ）が発生します。

では、どの程度永久ひずみが発生するのでしょうか？

それは、応力-ひずみ線図から作図をして求めることができます。

たとえば、ひずみが10%(0.1)のときの永久ひずみ量はどうなるかを作図すると、

1. ひずみ=0.1の位置に点を打つ。(点Pとする）
2. 点Pを通り、ヤング率と同じ傾きの直線を引く。(直線Lとする）
3. 直線Lと、x軸との交点が永久ひずみ量

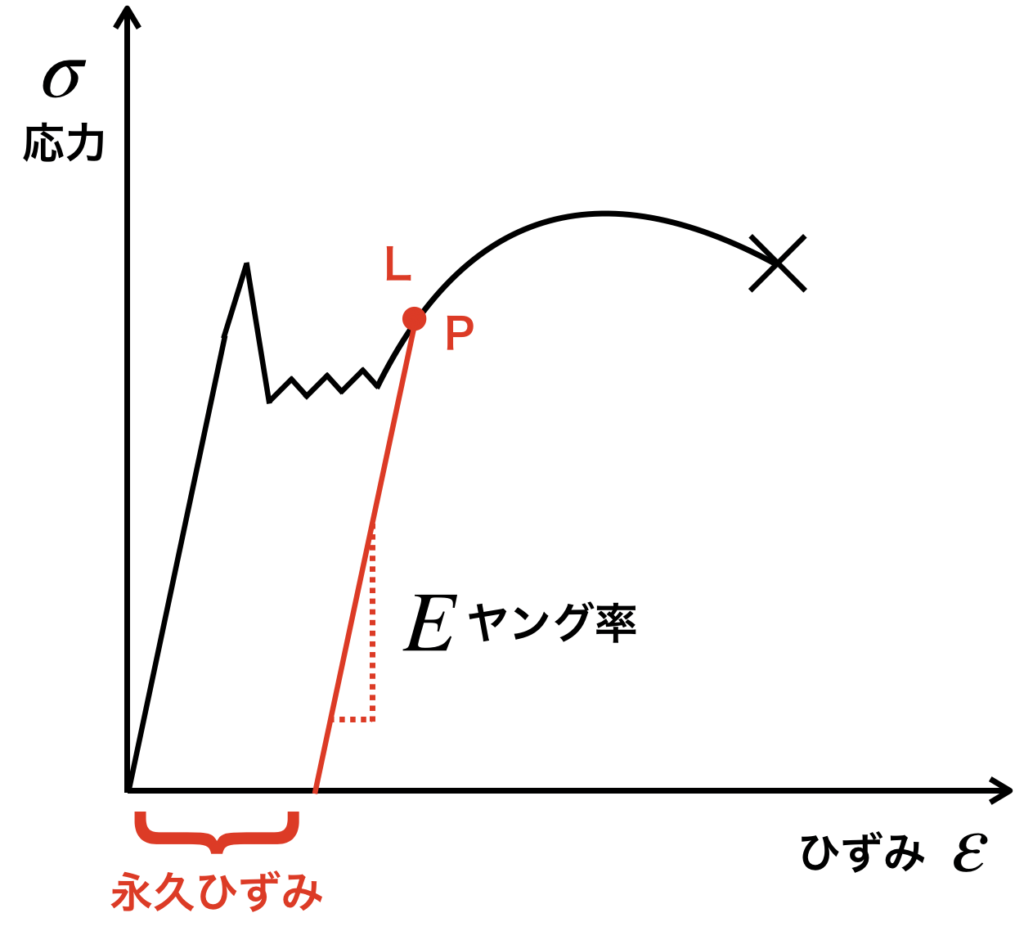
なぜ、これで永久ひずみ量が求められるのでしょうか？

材料を塑性領域の状態まで持って行き、荷重を0にしたとしても、
材料はその状態をキープするのではなく「元に戻れる範囲まで元に戻ろうとする」ためです。

どの程度元に戻ろうとするかは、弾性領域のグラフ形状が表しております。

そのため、この方法で永久ひずみがわかるのです。

降伏するかどうか

応力-ひずみ線図を見ることで、降伏するかどうかがわかります。

材料が降伏すると、まるで堤防が決壊したかのように、材料のひずみ及び永久ひずみが一気に進行します。

丈夫な部品を作る上で、材料が降伏する＝とても危険な状態なので、弾性領域内で範囲で設計をするのが一般的です。

しかし、実際には弾性限度の応力の測定は難しいため、その代わりに測定がしやすい降伏点（降伏応力）を測定し、
「降伏応力0.xx倍の応力を上限とする」ことが多いです。

このように、設計をする上で、材料に発生しても問題ないとする応力の上限のことを許容応力といいます。

しかし、材料の中には、そもそも降伏しない材料があります。
代表的なのは「アルミ」や「ステンレス」です。

これらの応力・ひずみ線図は、以下のような形状をしております。

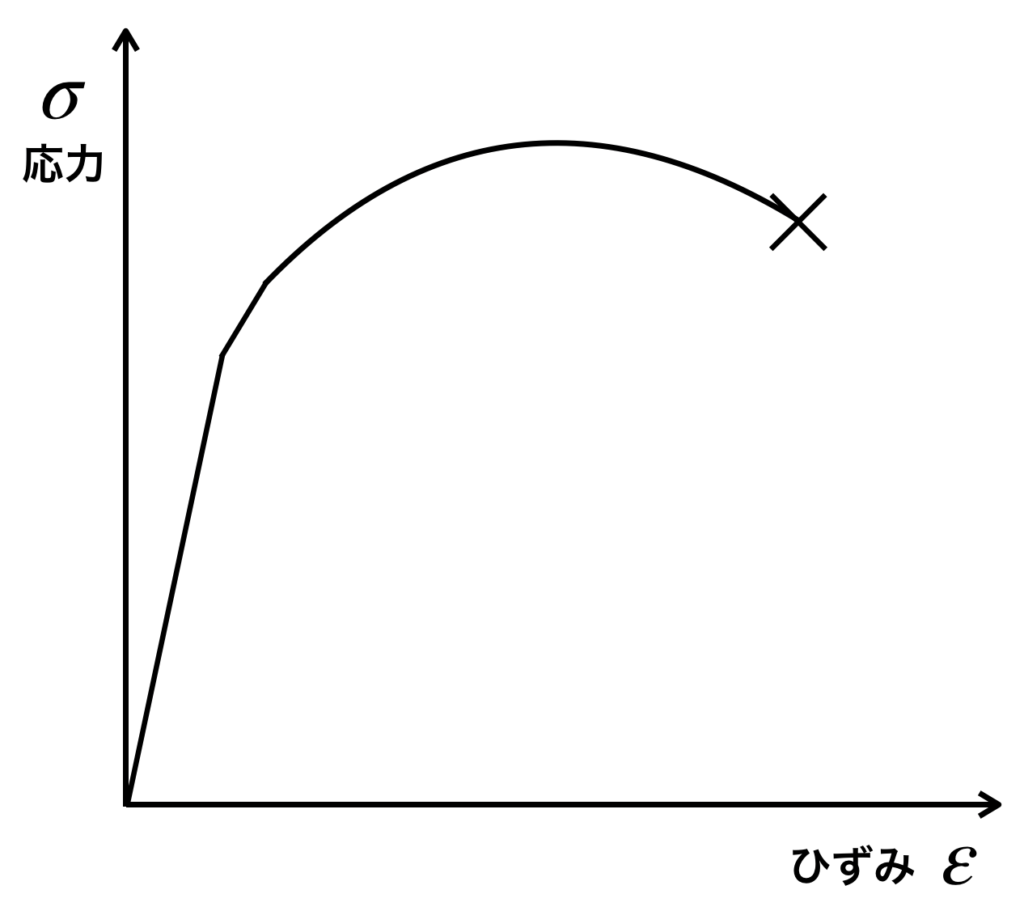
このような場合、どのように許容応力を決定すれば良いのでしょうか？

答えは、「永久ひずみが0.2%(0.002)となる時の応力＝降伏応力相当」とするのが、一般的です。
この応力を0.2%耐力といいます。

「設計の際は、0.2%耐力の0.xx倍を許容応力とする」といったように、ものづくりでは使われます。

「なぜ0.2%という数字がでてきたのか」というのは、明確な理由がないのですが、

一説では「降伏する材料の降伏点が、だいたい永久ひずみ0.2%の場所に位置するから」と言われているようです。

ちなみに、降伏しない材料の許容応力を、中には0.5%にしているものもあるようですが、
日本国内では、「耐力＝0.2%の永久ひずみ」が一般的です。

材料の壊れ方

軟鋼の応力-ひずみ線図と、ガラスの応力-ひずみ線図を比べてみましょう。

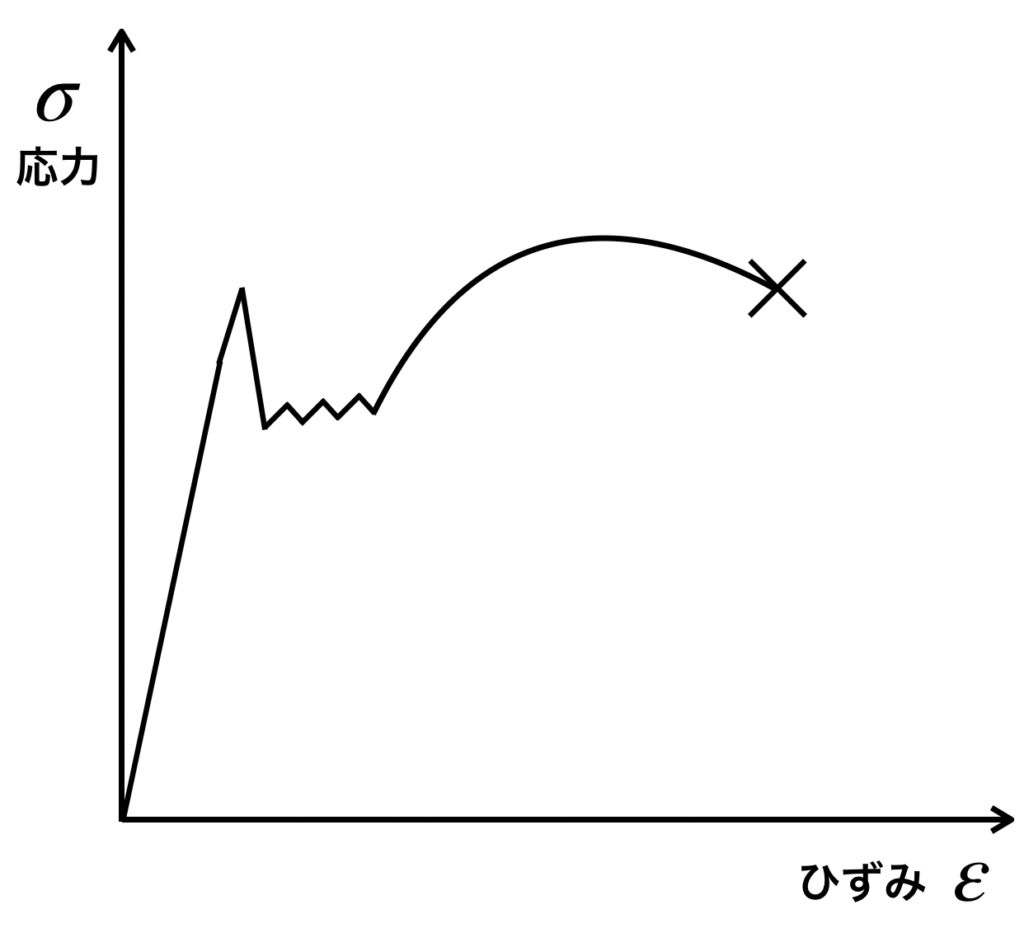
ここで注目してほしいのは、引張強さ（最大応力）を超えてから、破断点までの線図です。

軟鋼では、引張強さを超えると材料が大きくひずんでいることがわかります。
つまり、材料が伸びながら壊れることを意味します。

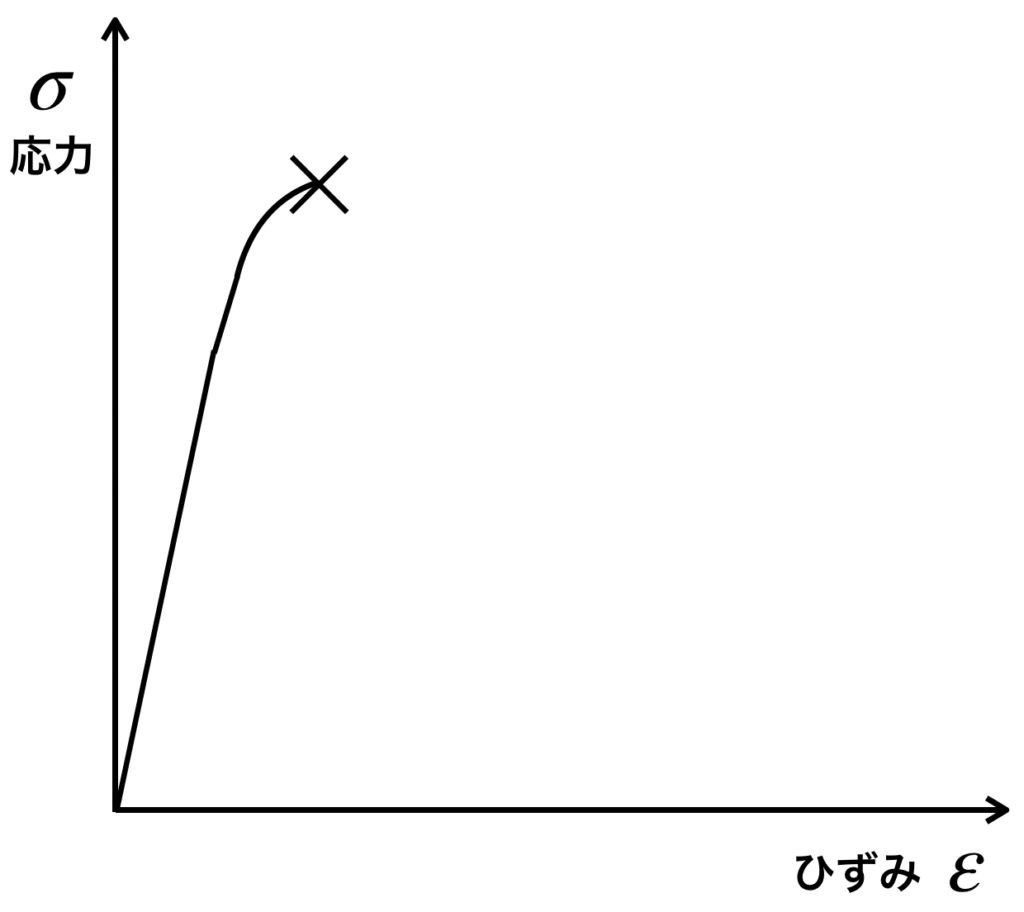
一方ガラスでは、引張強さと破断点がほぼ同じ点です。
つまり、ほとんど伸びることなくパキっと壊れることを意味します。

このような情報は、たとえば部品が壊れた時に、それがなぜ壊れたのかを分析するのに役に立ちます。

そもそも、グラフに使われる「応力」や「ひずみ」の種類って何？

そもそも、応力-ひずみ線図に使われている応力やひずみの種類は何でしょうか？

作ろうと思えば、どのような種類の応力-ひずみについての線図も作れますが、世の中にある線図の99%は「引張応力-引張ひずみの線図」です。

これはJISという日本の規格で定められた方法で測定をして線図を得るのですが、この試験のことを引張試験と呼びます。

ちなみに、圧縮応力やせん断応力の場合は、引張試験によって得られた線図をそのまま適用することはできません。

適用をするには、引張試験のデータに係数をかけた値を使用することが多いです。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...