図面に描かれた形状・寸法とおりに部品が製作されているかどうかを確かめる工程が検査です。
「ものづくりといえば設計」で、「検査はおまけのようなもの」、といったような考えをお持ちの人もたまに見かけますが、この「検査」の知識は、実はとても奥が深いのです。
検査の知識を知っているかどうかで、設計の質が左右されることも、多くあります。
例として、モーターを使った装置によく使われる軸(シャフト)について考えてみましょう。
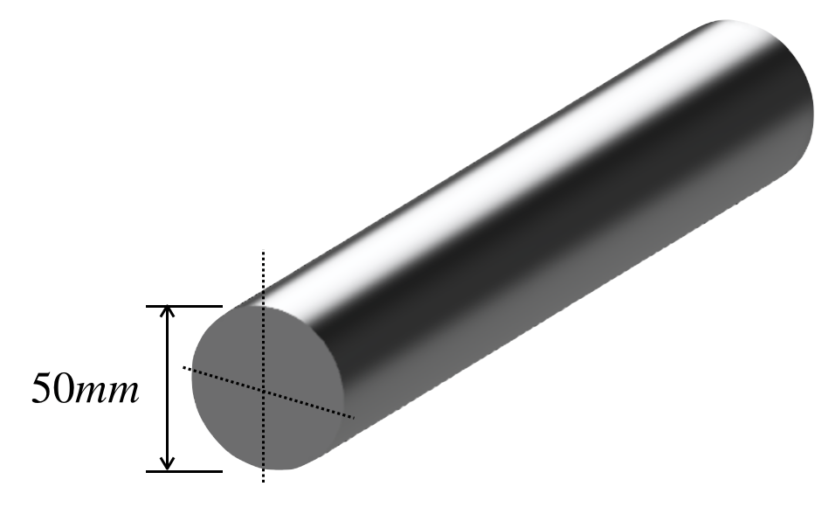
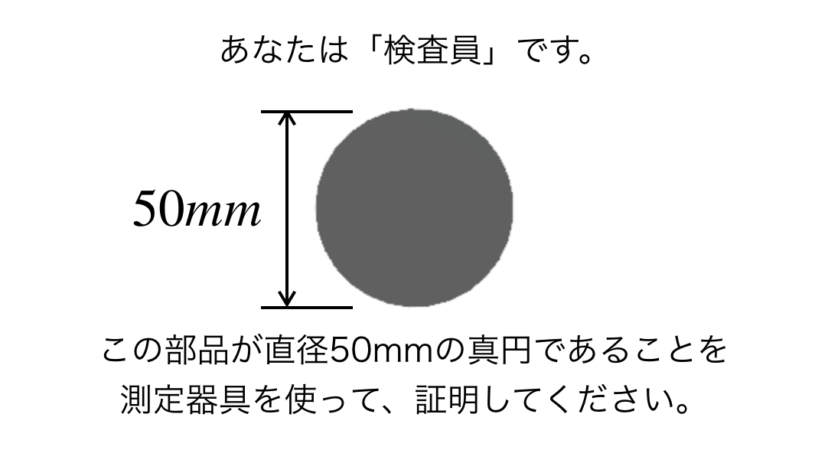
図面には、「直径50mmで真円の円柱形状」のシャフトが描かれています(この例では、シャフトの長さは任意とします)。
そして、製作メーカーに依頼して、この部品を作ってもらいました。
さて、部品ができあがりましたが、この部品が「直径50mmで真円の円柱形状」になっているかどうかを、あなたはどのように確かめますか?
この例を使って、今回はものづくりの検査の一部についてお話ししていきます。
手軽に寸法を測れる測定工具であるノギスを使ってみましょう。
では、ノギスでシャフトの直径を1回測定し、それが50mmであった場合、果たしてこの部品は直径50mmで真円の円柱形状のシャフトになっていると言えるでしょうか?
答えはNoです。
なぜなら、シャフトが楕円形状になっている可能性を否定できていないためです。
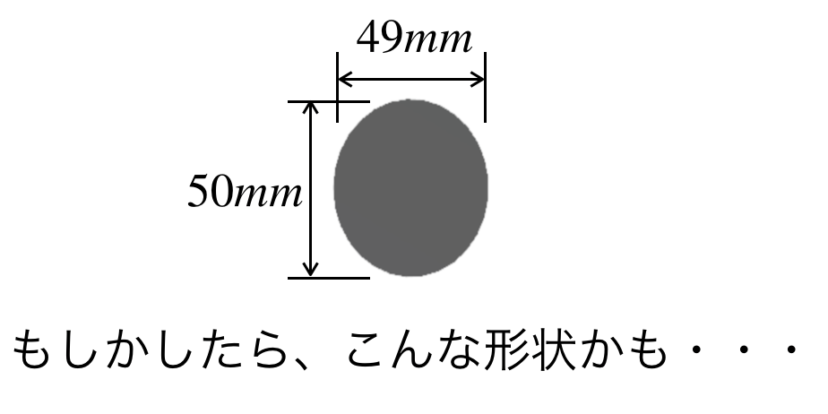
今度は、ノギスを当てる角度が異なる2箇所で、シャフトの直径を測定します。
これで2回とも測定結果が50mmであった場合、果たしてこの部品は、直径50mmで真円の円筒形状のシャフトであると言えるでしょうか?
答えはNoです。
なぜならば、シャフトが定幅図形になっている可能性を否定できないからです。
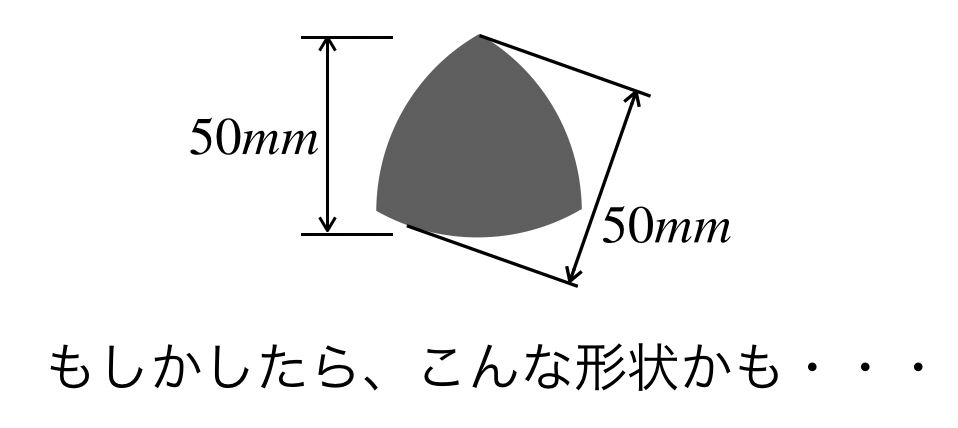
定幅図形とは、どの方向から測定しても、幅が一定である図形のことを言います。
円も定幅図形ではありますが、もう一つ有名な定幅図形として「ルーローの三角形」が挙げられます。
ルーローの三角形は、三角形の頂点同士が曲線で結ばれており、その曲線の中心が、向かい合う頂点となっているのが特徴です。
Panasonic製お掃除ロボットの「ルーロ」は、このルーローの三角形から商品名がつけられております。
また、マツダのロータリーエンジンのローターにも、このルーローの三角形が利用されております。
幅が一定なので、2本の平行線の間を、円と同様に転がることができます。
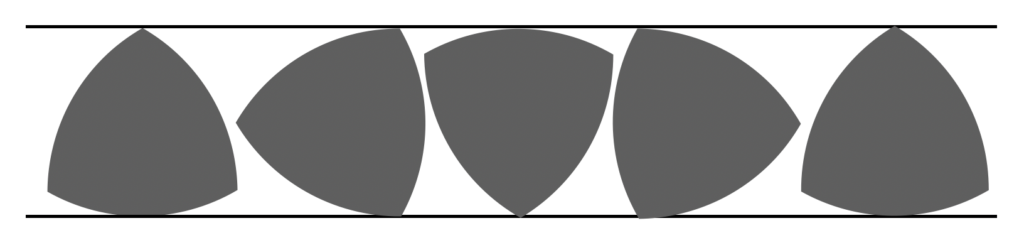
つまり、どの方向から測定しても幅が一定であることから、たとえ10回測定した結果がすべて50mmであったとしても、真円を証明することはできません。
ルーローの三角形であれば、見分けがつくかもしれませんが、このような図形は「2n+1角形(奇数角形)」ごとに存在するため、2n+1の数値が大きいものほど、円との見分けがつきにくくなります。
では、どうすれば真円が証明できるでしょうか?
最も簡単なのは、V字ブロックとダイヤルゲージを利用する方法です。
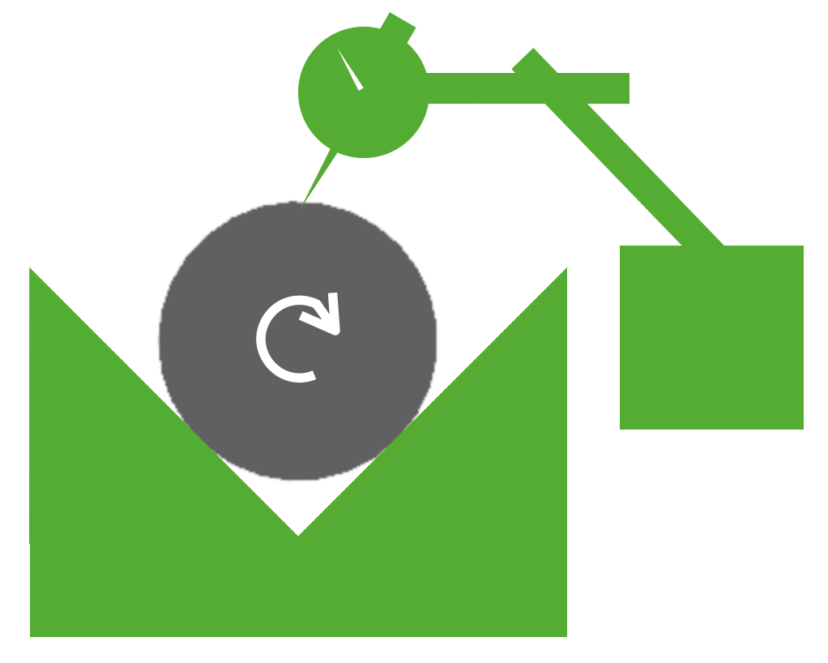
V字ブロックとは、その名の通り、V字の溝が設けられているブロックです。
また、ダイヤルゲージとは、ばねにより出戻りする針の変動を検知する測定器具で、1/100mm程度の細かい変動も検知できるものです。
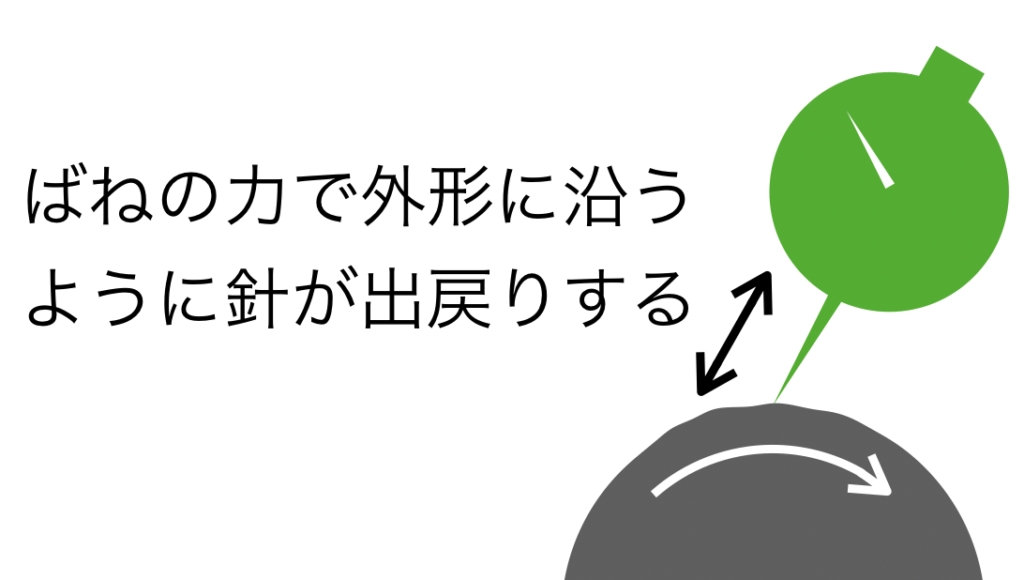
ダイヤルゲージを当てながら部品を回して行った時に、ダイヤルゲージの変動がなければ、真円であることが証明されます。
(実際には変動がまったく0ということはあり得ないので、変動が許容値以内であればOKという判断になります)
なぜこの方法で真円が証明できるか?
それは「測定基準の違い」です。
ノギスでの測定ですと、部品の外形を基準としてしまうので、円とルーローの三角形との違いを識別できません。
一方V字ブロックに部品を乗せると、V字ブロックと部品との接点を基準とすることができます。
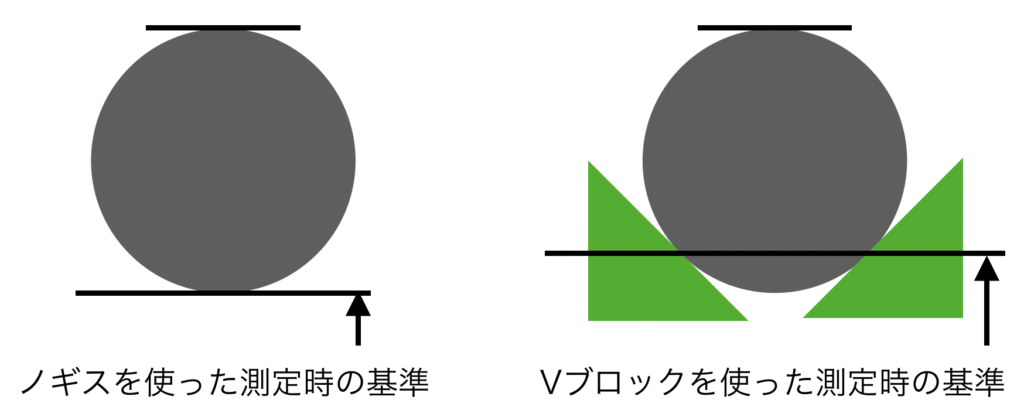
円の場合はV字ブロックに乗せて回転させても高さ変わりませんが、ルーローの三角形の場合は、回転角によって高さが変動します。
ただし、この方法単体では「真円の検査」はできますが、「直径が50mmかどうか」という検査はできません。
そのため、ノギスなどによる外径の測定器具と併用する必要があります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

アッべの原理と誤差【その測定結果を信用しても大丈夫ですか?】