
今までは、材料に直接的に力を与えるという議論をしてきましたが、
今回は、材料に「熱」を加わったときの、材料の状態について考えていきます。
材料は熱を加えると膨張し、冷却をすると収縮します。
材料が、膨張や収縮をしようとしているにも関わらず、
材料が伸び縮みできないよう拘束されていると、
そこには応力が発生します。

これを熱応力と呼びます。
そんな熱応力について、今回はお話しします。
温度変化1℃あたり、どの程度ひずみが発生するかを表したのが、線膨張係数という値です。通常αという記号で表し、単位は[1/℃]です。
ひずみに単位がないため、単位の分子は「1」です。
この線膨張係数と、ひずみには以下のような関係式があります。
$$
\varepsilon_T=\alpha\Delta T
$$
εT:温度変化によるひずみ [-]
α:線膨張係数 [1/℃]
ΔT:温度変化 [℃]
ここで、ひずみが出てきておりますが、特に荷重が加わっていない場合は、材料に応力は発生しません(材料が伸びるだけです)。
この式の両辺に、材料の元の寸法をかけると、伸びの量を求めることができます。
$$\begin{align}
\varepsilon_TL=\Delta L =\alpha\cdot \Delta T L
\end{align}$$
$$\varepsilon=\frac{\Delta L}{L},\quad \varepsilon L=\Delta L$$
一方で、温度変化によって材料に外力が加わった場合、
例えば、棒の両端が断熱の壁に固定されている状態で、棒に熱が加わった場合には、
棒は膨張しようとしているにも関わらず、壁によって拘束されているので、棒には熱応力が発生します。

熱応力の問題は、不静定問題によく出てきますので、合わせて習得できるようにしておきたいですね。
ものづくりにおいて、熱応力による不具合は、たまに聞く話ではありますが、不具合が生じる根本的な原因は、線膨張係数の「差」です。
線膨張係数は、材質によって値が異なるのです。
例えば以下のように、軟鋼でできた板Aと、軟鋼でできた板Bとをボルトで固定します。
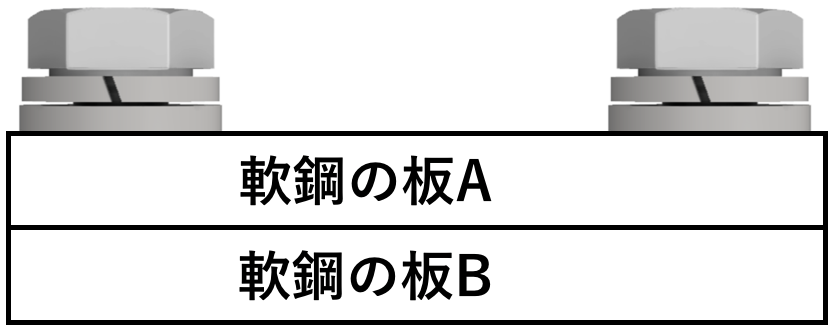

この状態で高温状態にさせると、軟鋼の板Aも軟鋼の板Bも膨張をします。
しかし、どちらの板も線膨張係数が同じであるため、どちらも同じように膨張し、応力は発生しません。
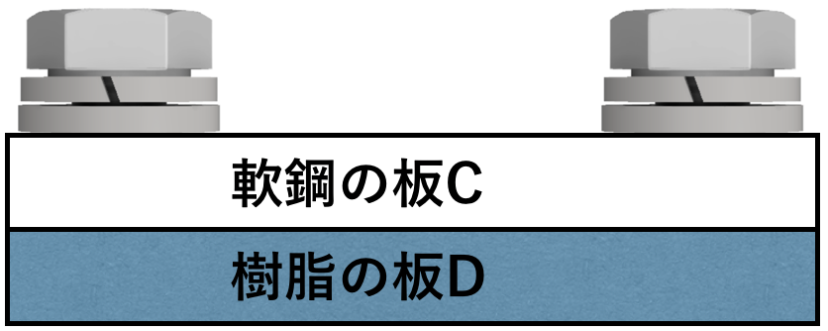
一方で、線膨張係数の小さい軟鋼の板Cと、線膨張係数の大きい樹脂の板Dとを、ボルトで固定したものを考えます。
この状態から、何らかの要因(炎天下や寒波)で温度変化が発生すると、
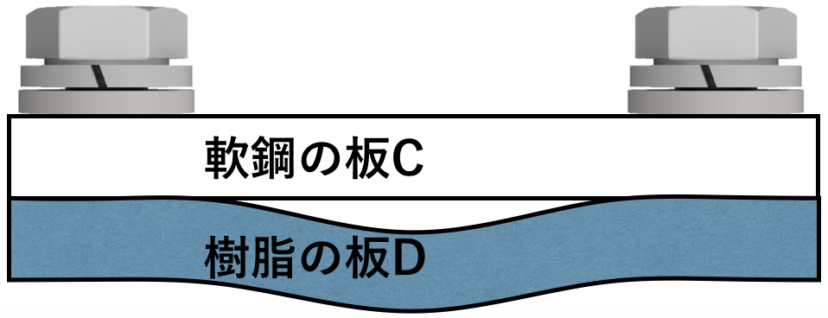
樹脂の板Dは大きく膨張しようとしますが、軟鋼の板Cはあまり膨張しようとしませんから、
板Dには圧縮応力が、板Cには引張応力が発生します。
一般的に樹脂の方がヤング率が低いわけですから、樹脂の板Dの方が曲がったり、割れたりします。
対策をするには、
あたりを検討することが多いです。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


材料力学 演習問題 02【棒の応力とひずみ】
釣り合いの式だけでは解けない、不静定問題の解き方
