|
|
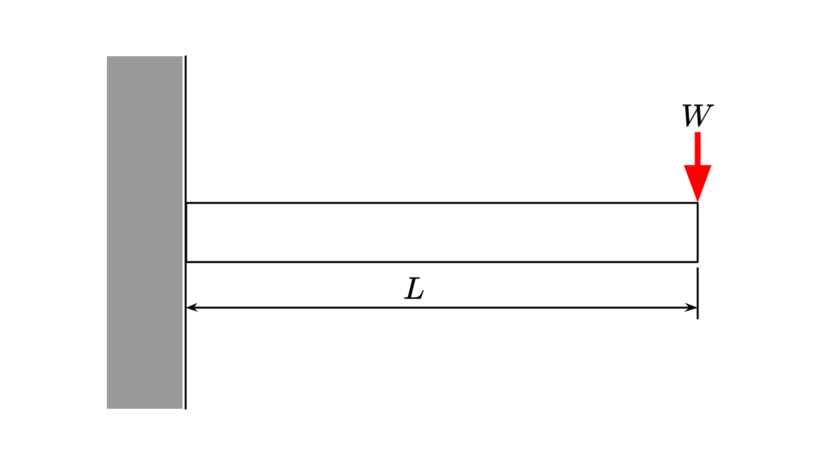
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
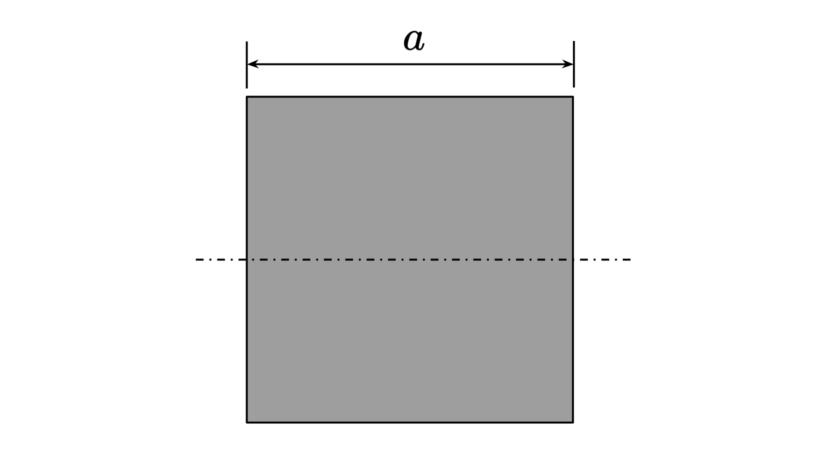
| 一辺の長さ | $$a$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4}{12}\\Z=\frac{a^3}{6}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|
|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
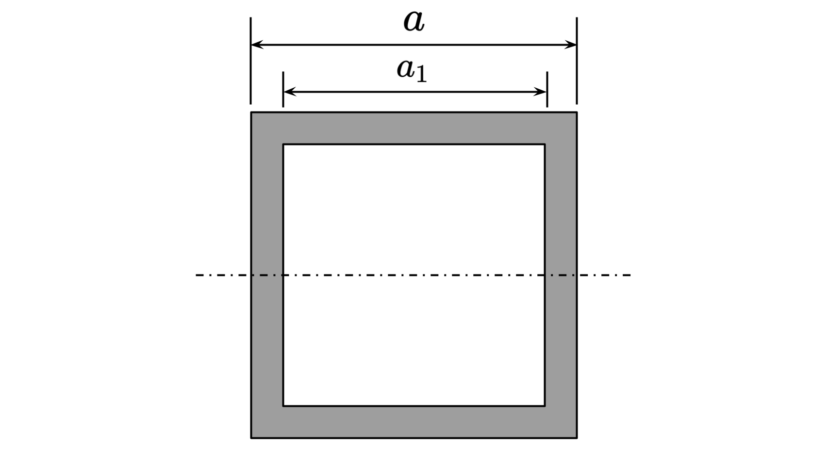
| 外幅 内幅 |
$$\begin{align}a\\a_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4-a_1^4}{12}\\Z=\frac{a^4-a_1^4}{6a}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3}{12}\\Z=\frac{bh^2}{6}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|
|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
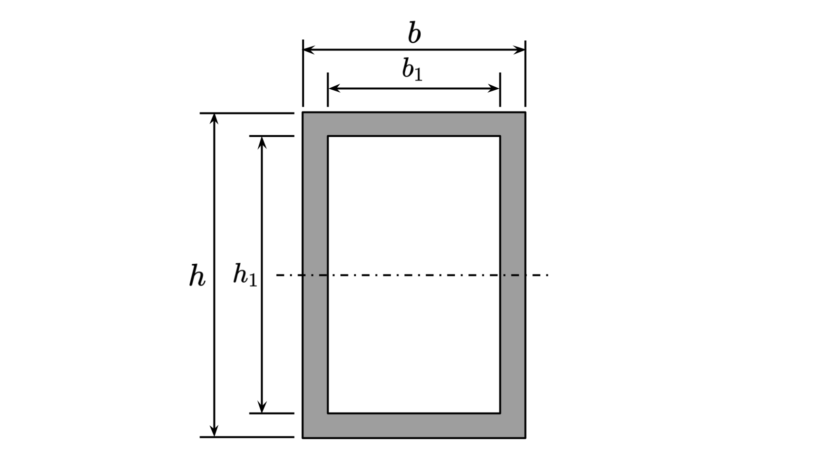
| 外幅 内幅 外高さ 内高さ |
$$\begin{align}b\\b_1\\h\\h_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-b_1h_1^3}{12}\\Z=\frac{bh^3-b_1h_1^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|
|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
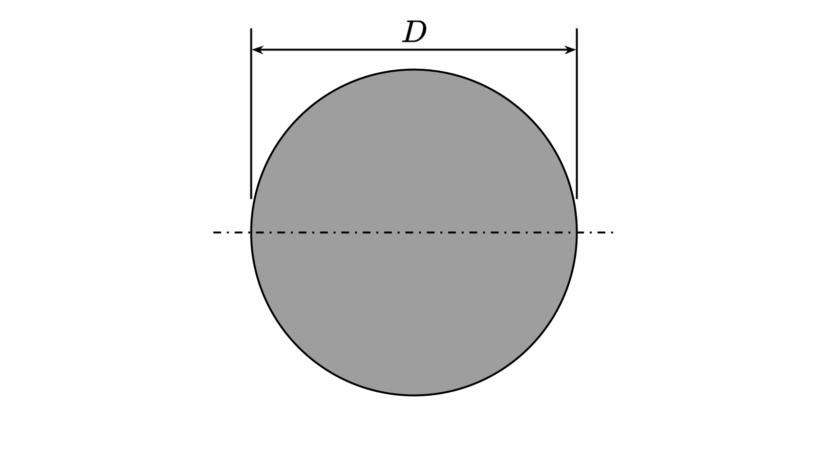
| 径 | $$D$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi D^4}{64}\\Z=\frac{\pi D^3}{32}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|
|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
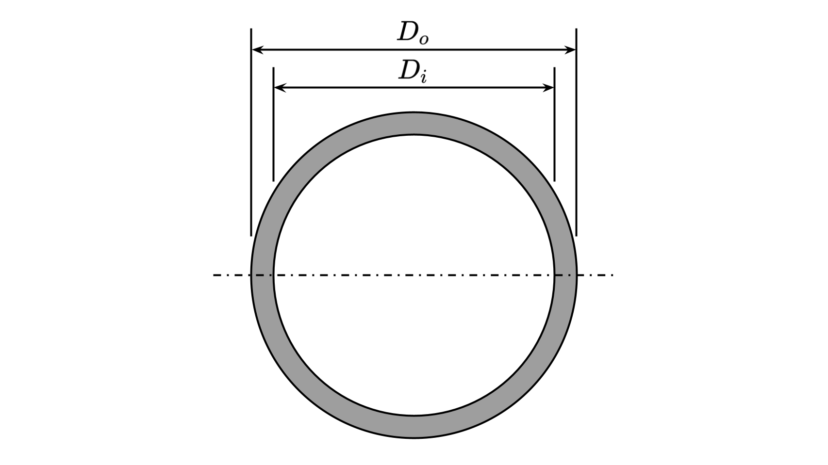
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi(D_o^4-D_i^4)}{64}\\Z=\frac{\pi(D_o^4-D_i^4)}{32D_o}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|
|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
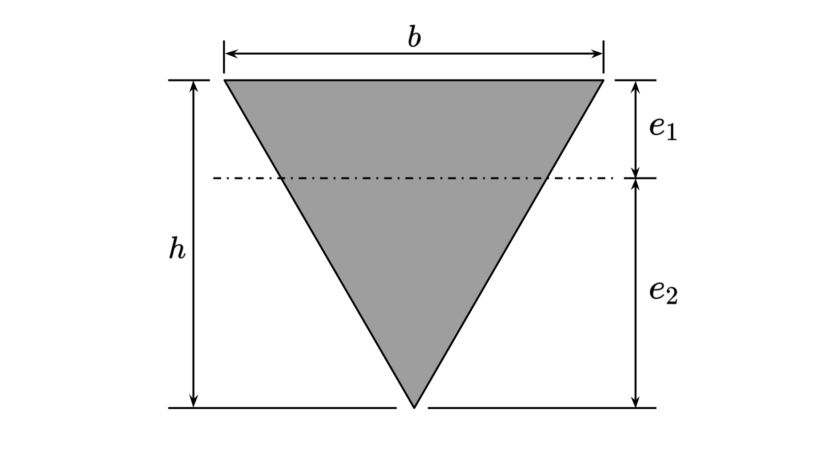
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{1}{3}h\\e_2&=\frac{2}{3}h\\I&=\frac{bh^3}{36}\\Z_1&=\frac{I}{e_1}=\frac{bh^2}{12}\\Z_2&=\frac{I}{e_2}=\frac{bh^2}{24}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_2}$$ |

|
|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
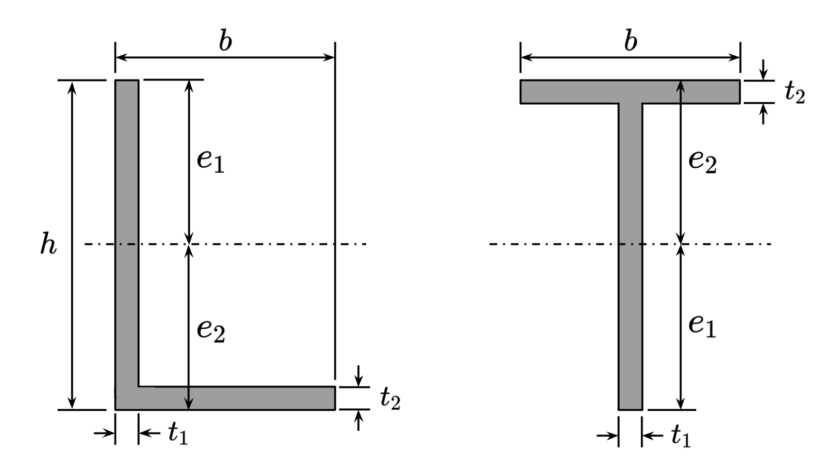
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{t_1h^2+2(b-t_1)t_2h-(b-t_1)t_2^2}{2(b-t_1)t_2+t_1h}\\e_2&=\frac{(b-t_1)t_2^2+t_1h^2}{2(b-t_1)t_2+t_1h}\\I&=\frac{1}{3}(be_2^3-(b-t_1)(e_2-t_2)^3+t_2e_1^3)\\Z_1&=\frac{I}{e_1}\\Z_2&=\frac{I}{e_2}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_1}$$ |

|
|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
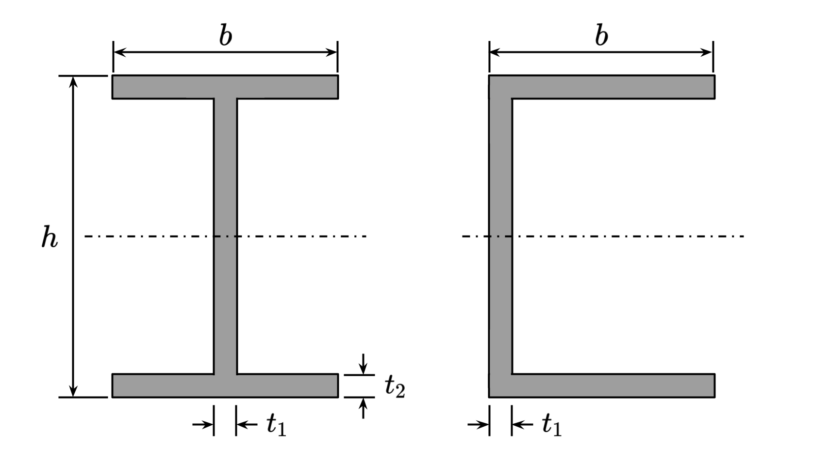
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-t_1)(h-2t_2)^3}{12}\\Z=\frac{bh^3-(b-t_1)(h-2t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|
|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
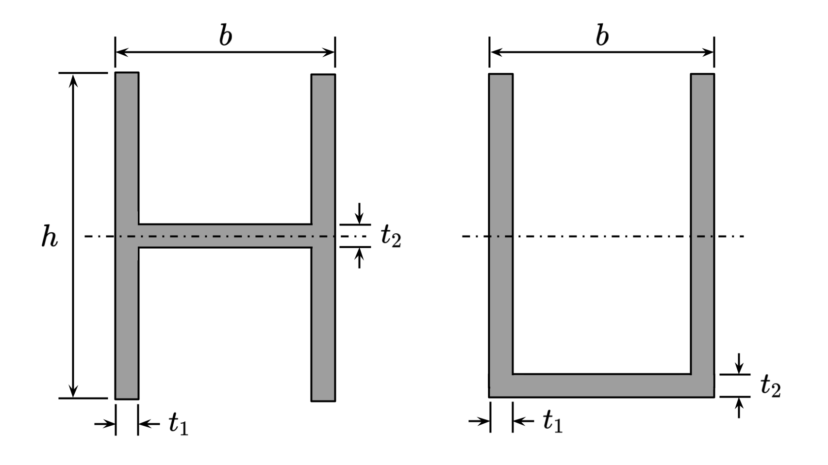
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-2t_1)(h-t_2)^3}{12}\\Z=\frac{bh^3-(b-2t_1)(h-t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 断面二次モーメント 断面係数 |
$$\begin{align}I\\Z\end{align}$$ | |
| 反力 | $$R=W$$ | ||
| 最大曲げモーメント | $$M=WL$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{3EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |
|

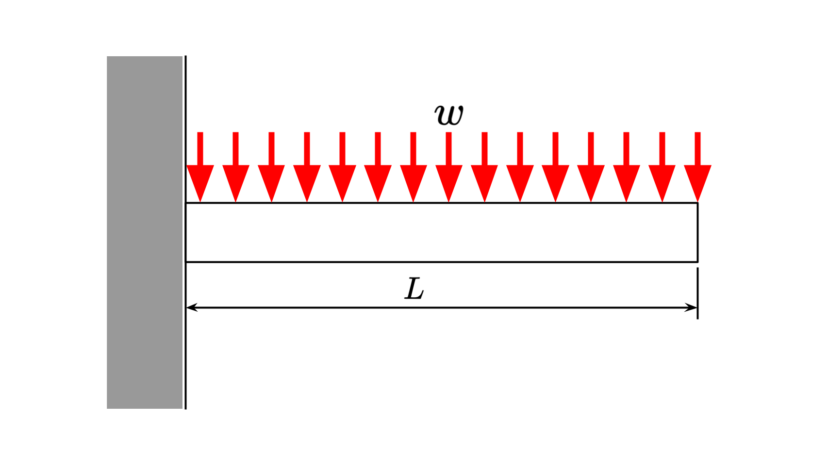
|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 一辺の長さ | $$a$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4}{12}\\Z=\frac{a^3}{6}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 |
$$\begin{align}a\\a_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4-a_1^4}{12}\\Z=\frac{a^4-a_1^4}{6a}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3}{12}\\Z=\frac{bh^2}{6}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 外高さ 内高さ |
$$\begin{align}b\\b_1\\h\\h_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-b_1h_1^3}{12}\\Z=\frac{bh^3-b_1h_1^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 径 | $$D$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi D^4}{64}\\Z=\frac{\pi D^3}{32}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi(D_o^4-D_i^4)}{64}\\Z=\frac{\pi(D_o^4-D_i^4)}{32D_o}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{1}{3}h\\e_2&=\frac{2}{3}h\\I&=\frac{bh^3}{36}\\Z_1&=\frac{I}{e_1}=\frac{bh^2}{12}\\Z_2&=\frac{I}{e_2}=\frac{bh^2}{24}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_2}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{t_1h^2+2(b-t_1)t_2h-(b-t_1)t_2^2}{2(b-t_1)t_2+t_1h}\\e_2&=\frac{(b-t_1)t_2^2+t_1h^2}{2(b-t_1)t_2+t_1h}\\I&=\frac{1}{3}(be_2^3-(b-t_1)(e_2-t_2)^3+t_2e_1^3)\\Z_1&=\frac{I}{e_1}\\Z_2&=\frac{I}{e_2}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_1}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-t_1)(h-2t_2)^3}{12}\\Z=\frac{bh^3-(b-t_1)(h-2t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-2t_1)(h-t_2)^3}{12}\\Z=\frac{bh^3-(b-2t_1)(h-t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 断面二次モーメント 断面係数 |
$$\begin{align}I\\Z\end{align}$$ | |
| 反力 | $$R=wL$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |
|

|
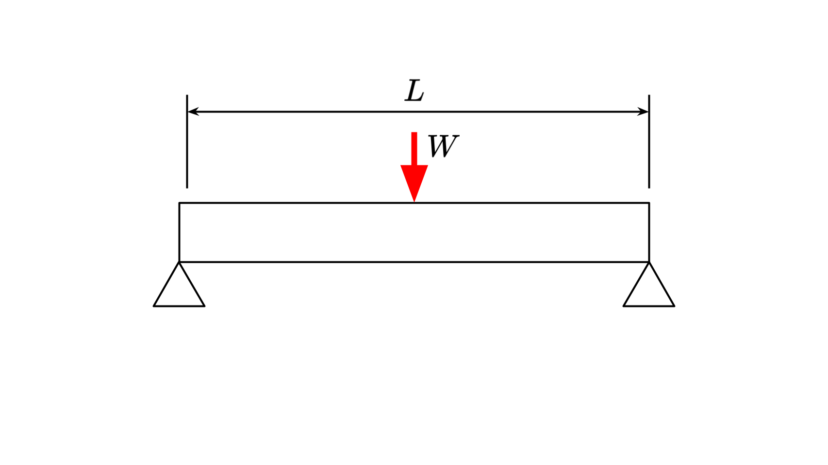
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 一辺の長さ | $$a$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4}{12}\\Z=\frac{a^3}{6}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 |
$$\begin{align}a\\a_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4-a_1^4}{12}\\Z=\frac{a^4-a_1^4}{6a}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3}{12}\\Z=\frac{bh^2}{6}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 外高さ 内高さ |
$$\begin{align}b\\b_1\\h\\h_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-b_1h_1^3}{12}\\Z=\frac{bh^3-b_1h_1^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 径 | $$D$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi D^4}{64}\\Z=\frac{\pi D^3}{32}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi(D_o^4-D_i^4)}{64}\\Z=\frac{\pi(D_o^4-D_i^4)}{32D_o}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{1}{3}h\\e_2&=\frac{2}{3}h\\I&=\frac{bh^3}{36}\\Z_1&=\frac{I}{e_1}=\frac{bh^2}{12}\\Z_2&=\frac{I}{e_2}=\frac{bh^2}{24}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_2}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{t_1h^2+2(b-t_1)t_2h-(b-t_1)t_2^2}{2(b-t_1)t_2+t_1h}\\e_2&=\frac{(b-t_1)t_2^2+t_1h^2}{2(b-t_1)t_2+t_1h}\\I&=\frac{1}{3}(be_2^3-(b-t_1)(e_2-t_2)^3+t_2e_1^3)\\Z_1&=\frac{I}{e_1}\\Z_2&=\frac{I}{e_2}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_1}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-t_1)(h-2t_2)^3}{12}\\Z=\frac{bh^3-(b-t_1)(h-2t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-2t_1)(h-t_2)^3}{12}\\Z=\frac{bh^3-(b-2t_1)(h-t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 断面二次モーメント 断面係数 |
$$\begin{align}I\\Z\end{align}$$ | |
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{4}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |
|

|
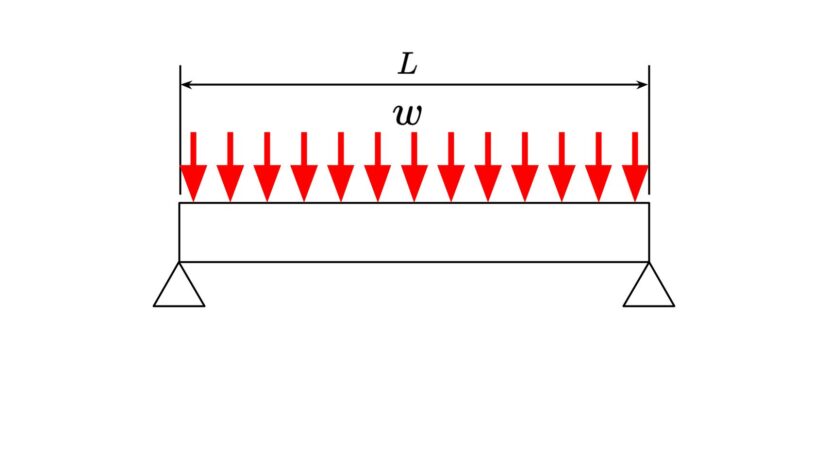
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 一辺の長さ | $$a$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4}{12}\\Z=\frac{a^3}{6}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 |
$$\begin{align}a\\a_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4-a_1^4}{12}\\Z=\frac{a^4-a_1^4}{6a}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3}{12}\\Z=\frac{bh^2}{6}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 外高さ 内高さ |
$$\begin{align}b\\b_1\\h\\h_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-b_1h_1^3}{12}\\Z=\frac{bh^3-b_1h_1^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 径 | $$D$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi D^4}{64}\\Z=\frac{\pi D^3}{32}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi(D_o^4-D_i^4)}{64}\\Z=\frac{\pi(D_o^4-D_i^4)}{32D_o}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{1}{3}h\\e_2&=\frac{2}{3}h\\I&=\frac{bh^3}{36}\\Z_1&=\frac{I}{e_1}=\frac{bh^2}{12}\\Z_2&=\frac{I}{e_2}=\frac{bh^2}{24}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_2}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{t_1h^2+2(b-t_1)t_2h-(b-t_1)t_2^2}{2(b-t_1)t_2+t_1h}\\e_2&=\frac{(b-t_1)t_2^2+t_1h^2}{2(b-t_1)t_2+t_1h}\\I&=\frac{1}{3}(be_2^3-(b-t_1)(e_2-t_2)^3+t_2e_1^3)\\Z_1&=\frac{I}{e_1}\\Z_2&=\frac{I}{e_2}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_1}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-t_1)(h-2t_2)^3}{12}\\Z=\frac{bh^3-(b-t_1)(h-2t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-2t_1)(h-t_2)^3}{12}\\Z=\frac{bh^3-(b-2t_1)(h-t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 断面二次モーメント 断面係数 |
$$\begin{align}I\\Z\end{align}$$ | |
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{wL^2}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{5wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |
|

|
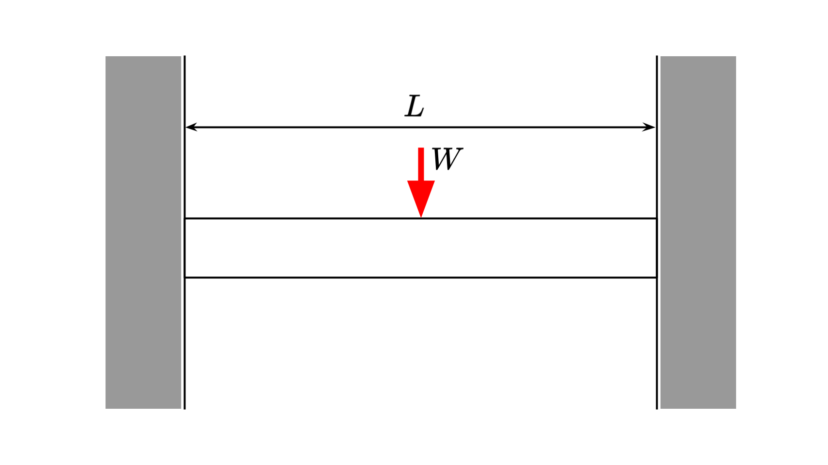
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 一辺の長さ | $$a$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4}{12}\\Z=\frac{a^3}{6}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 |
$$\begin{align}a\\a_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4-a_1^4}{12}\\Z=\frac{a^4-a_1^4}{6a}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3}{12}\\Z=\frac{bh^2}{6}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 外高さ 内高さ |
$$\begin{align}b\\b_1\\h\\h_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-b_1h_1^3}{12}\\Z=\frac{bh^3-b_1h_1^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 径 | $$D$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi D^4}{64}\\Z=\frac{\pi D^3}{32}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi(D_o^4-D_i^4)}{64}\\Z=\frac{\pi(D_o^4-D_i^4)}{32D_o}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{1}{3}h\\e_2&=\frac{2}{3}h\\I&=\frac{bh^3}{36}\\Z_1&=\frac{I}{e_1}=\frac{bh^2}{12}\\Z_2&=\frac{I}{e_2}=\frac{bh^2}{24}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_2}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{t_1h^2+2(b-t_1)t_2h-(b-t_1)t_2^2}{2(b-t_1)t_2+t_1h}\\e_2&=\frac{(b-t_1)t_2^2+t_1h^2}{2(b-t_1)t_2+t_1h}\\I&=\frac{1}{3}(be_2^3-(b-t_1)(e_2-t_2)^3+t_2e_1^3)\\Z_1&=\frac{I}{e_1}\\Z_2&=\frac{I}{e_2}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_1}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-t_1)(h-2t_2)^3}{12}\\Z=\frac{bh^3-(b-t_1)(h-2t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-2t_1)(h-t_2)^3}{12}\\Z=\frac{bh^3-(b-2t_1)(h-t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 断面二次モーメント 断面係数 |
$$\begin{align}I\\Z\end{align}$$ | |
| 反力 | $$R=\frac{W}{2}$$ | ||
| 最大曲げモーメント | $$M=\frac{WL}{8}$$ | ||
| 最大たわみ | $$\delta=\frac{WL^3}{192EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |
|

|
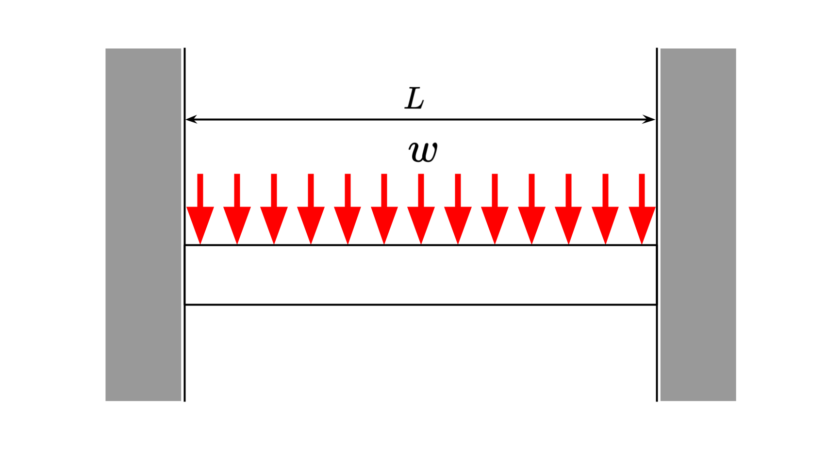
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 一辺の長さ | $$a$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4}{12}\\Z=\frac{a^3}{6}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 |
$$\begin{align}a\\a_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4-a_1^4}{12}\\Z=\frac{a^4-a_1^4}{6a}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3}{12}\\Z=\frac{bh^2}{6}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 外高さ 内高さ |
$$\begin{align}b\\b_1\\h\\h_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-b_1h_1^3}{12}\\Z=\frac{bh^3-b_1h_1^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 径 | $$D$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi D^4}{64}\\Z=\frac{\pi D^3}{32}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi(D_o^4-D_i^4)}{64}\\Z=\frac{\pi(D_o^4-D_i^4)}{32D_o}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{1}{3}h\\e_2&=\frac{2}{3}h\\I&=\frac{bh^3}{36}\\Z_1&=\frac{I}{e_1}=\frac{bh^2}{12}\\Z_2&=\frac{I}{e_2}=\frac{bh^2}{24}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_2}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{t_1h^2+2(b-t_1)t_2h-(b-t_1)t_2^2}{2(b-t_1)t_2+t_1h}\\e_2&=\frac{(b-t_1)t_2^2+t_1h^2}{2(b-t_1)t_2+t_1h}\\I&=\frac{1}{3}(be_2^3-(b-t_1)(e_2-t_2)^3+t_2e_1^3)\\Z_1&=\frac{I}{e_1}\\Z_2&=\frac{I}{e_2}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_1}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-t_1)(h-2t_2)^3}{12}\\Z=\frac{bh^3-(b-t_1)(h-2t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-2t_1)(h-t_2)^3}{12}\\Z=\frac{bh^3-(b-2t_1)(h-t_2)^3}{6h}\end{align}$$ | |
|
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 断面二次モーメント 断面係数 |
$$\begin{align}I\\Z\end{align}$$ | |
| 反力 | $$R=\frac{wL}{2}$$ | ||
| 最大曲げモーメント | $$M=-\frac{wL^2}{12}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{384EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |
|

|
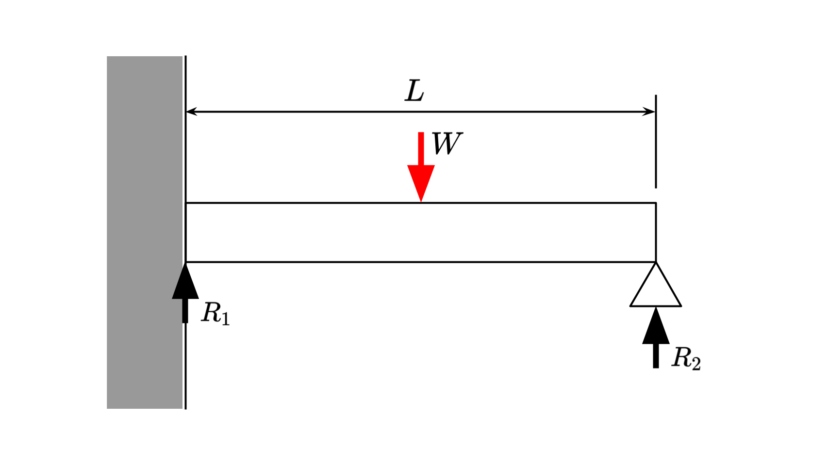
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 一辺の長さ | $$a$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4}{12}\\Z=\frac{a^3}{6}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | ||
| 反力2 | $$R_2=\frac{5W}{16}$$ | ||
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 |
$$\begin{align}a\\a_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4-a_1^4}{12}\\Z=\frac{a^4-a_1^4}{6a}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3}{12}\\Z=\frac{bh^2}{6}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 外高さ 内高さ |
$$\begin{align}b\\b_1\\h\\h_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-b_1h_1^3}{12}\\Z=\frac{bh^3-b_1h_1^3}{6h}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 径 | $$D$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi D^4}{64}\\Z=\frac{\pi D^3}{32}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi(D_o^4-D_i^4)}{64}\\Z=\frac{\pi(D_o^4-D_i^4)}{32D_o}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{1}{3}h\\e_2&=\frac{2}{3}h\\I&=\frac{bh^3}{36}\\Z_1&=\frac{I}{e_1}=\frac{bh^2}{12}\\Z_2&=\frac{I}{e_2}=\frac{bh^2}{24}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_2}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{t_1h^2+2(b-t_1)t_2h-(b-t_1)t_2^2}{2(b-t_1)t_2+t_1h}\\e_2&=\frac{(b-t_1)t_2^2+t_1h^2}{2(b-t_1)t_2+t_1h}\\I&=\frac{1}{3}(be_2^3-(b-t_1)(e_2-t_2)^3+t_2e_1^3)\\Z_1&=\frac{I}{e_1}\\Z_2&=\frac{I}{e_2}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_1}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-t_1)(h-2t_2)^3}{12}\\Z=\frac{bh^3-(b-t_1)(h-2t_2)^3}{6h}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-2t_1)(h-t_2)^3}{12}\\Z=\frac{bh^3-(b-2t_1)(h-t_2)^3}{6h}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

| 集中荷重 | $$W$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 断面二次モーメント 断面係数 |
$$\begin{align}I\\Z\end{align}$$ | |
| 反力1 反力2 |
$$\begin{align}R_1=\frac{11W}{16}\\R_2=\frac{5W}{16}\end{align}$$ | |
|
| 最大曲げモーメント | $$M=-\frac{3WL}{16}$$ | ||
| 最大たわみ | $$\delta=\sqrt{\frac{1}{5}}\frac{WL^3}{48EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |
|

|
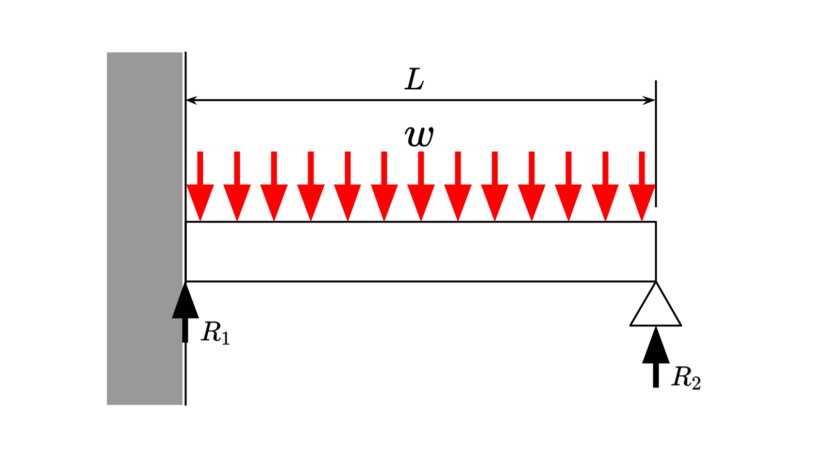
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 一辺の長さ | $$a$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4}{12}\\Z=\frac{a^3}{6}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 |
$$\begin{align}a\\a_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{a^4-a_1^4}{12}\\Z=\frac{a^4-a_1^4}{6a}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3}{12}\\Z=\frac{bh^2}{6}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外幅 内幅 外高さ 内高さ |
$$\begin{align}b\\b_1\\h\\h_1\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-b_1h_1^3}{12}\\Z=\frac{bh^3-b_1h_1^3}{6h}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 径 | $$D$$ |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi D^4}{64}\\Z=\frac{\pi D^3}{32}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 外径 内径 |
$$\begin{align}D_o\\D_i\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{\pi(D_o^4-D_i^4)}{64}\\Z=\frac{\pi(D_o^4-D_i^4)}{32D_o}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ |
$$\begin{align}b\\h\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{1}{3}h\\e_2&=\frac{2}{3}h\\I&=\frac{bh^3}{36}\\Z_1&=\frac{I}{e_1}=\frac{bh^2}{12}\\Z_2&=\frac{I}{e_2}=\frac{bh^2}{24}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_2}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 重心の距離 断面二次モーメント 断面係数 |
$$\begin{align}e_1&=\frac{t_1h^2+2(b-t_1)t_2h-(b-t_1)t_2^2}{2(b-t_1)t_2+t_1h}\\e_2&=\frac{(b-t_1)t_2^2+t_1h^2}{2(b-t_1)t_2+t_1h}\\I&=\frac{1}{3}(be_2^3-(b-t_1)(e_2-t_2)^3+t_2e_1^3)\\Z_1&=\frac{I}{e_1}\\Z_2&=\frac{I}{e_2}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z_1}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-t_1)(h-2t_2)^3}{12}\\Z=\frac{bh^3-(b-t_1)(h-2t_2)^3}{6h}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

|

|
| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 幅 高さ ウェブ厚さ フランジ厚さ |
$$\begin{align}b\\h\\t_1\\t_2\end{align}$$ | |
| 断面二次モーメント 断面係数 |
$$\begin{align}I=\frac{bh^3-(b-2t_1)(h-t_2)^3}{12}\\Z=\frac{bh^3-(b-2t_1)(h-t_2)^3}{6h}\end{align}$$ | |
|
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |

| 分布荷重 | $$w$$ | ||
| 梁の長さ | $$L$$ | ||
| ヤング率 | $$E$$ | ||
| 断面二次モーメント 断面係数 |
$$\begin{align}I\\Z\end{align}$$ | |
| 反力1 反力2 |
$$\begin{align}R_1=\frac{5}{8}wL\\R_2=\frac{3}{8}wL\end{align}$$ | |
|
| 最大曲げモーメント | $$M=\frac{wL^2}{2}$$ | ||
| 最大たわみ | $$\delta=\frac{wL^4}{8EI}$$ | ||
| 最大曲げ応力 | $$\sigma=\frac{M}{Z}$$ |
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

平行キー 強度計算ツール
座屈荷重・座屈応力 計算ツール