こんにちは!リヴィと申します!
普段は機械設計の仕事をしており、日本のものづくりに携わっております。
この記事を読むべき人
材料力学において、材料に力を加える方法というのは、「引張」「圧縮」「せん断」「曲げ」「ねじれ」の全部で5つありました(詳しくは以下の記事で解説しています)。
そして材料力学においては、材料が壊れないかどうかを判定するのに、荷重をそのまま使用するのではなく、「応力」というものを使って評価をします。
応力は以下のように定義されます。
$$応力=\frac{内力}{断面形状に関する値}$$
詳しくはこちら▼
ただ、材料力学を勉強していくとわかるのですが、応力にもいくつか種類があり、〇〇応力という名前の用語が多く出てきます。
そのせいで、それによって頭の中がごっちゃになってしまった人もいるかと思います。

「引張応力」とか「曲げ応力」とか「ミーゼス応力」とかっていうやつですね笑。
ただ実際には、応力は2種類しかなく、他の「〇〇応力」というのはこの2種類の組み合わせで成り立っているのです。
そこで今回は、応力の種類について、わかりやすく解説していきたいと思います。
今回の記事を読むと、材料の破壊の仕方などがイメージしやすくなりますので、ぜひ最後までご一読ください。
冒頭にも申し上げたとおり、本質的には応力の種類は2種類しかありません。
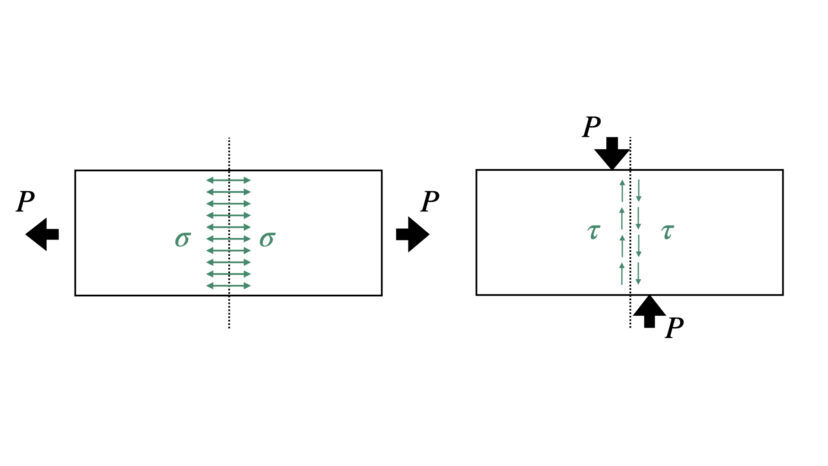
その2種類とは「垂直応力」と「せん断応力」です。
多くの教科書や参考書では、「引張応力」や「曲げ応力」といった言葉で説明されておりますが、これらは「垂直応力」の一種であったり、「垂直応力」と「せん断応力」組み合わせであったりします。
これを理解するためには、まずは「仮想断面」や「微小要素」といった概念を理解する必要があります。
材料力学では計算の便宜上のため、「仮想断面」や「微小要素」といった概念を使います。
仮想断面をわかりやすくいうと「問題を解く人のイメージの中でぶった切ったときの、材料の断面」ということです。
応力の式の右辺分母に「断面形状に関する値」があるように、計算をするためには、計算をする箇所の断面形状を知らなければなりません。
しかし、物理的に材料をぶった切って断面の形状を見るとなると、物理的にぶった切る段階で材料を壊さなければなりません。
そこで、あくまで問題を解く人のイメージの中だけで材料をぶった切った断面である「仮想断面」を使って計算するのです。
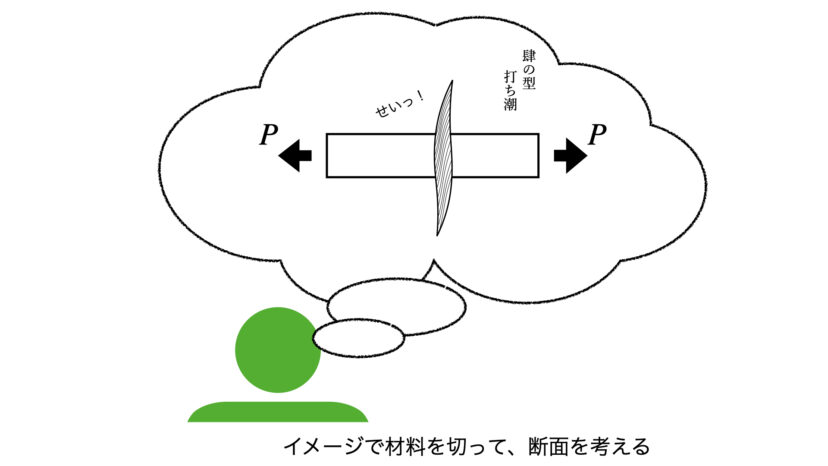

「仮想断面」というと難しく聞こえますが、「仮に、想像の中でぶった切った断面」と考えればよいかと思います。
一方で「微小要素」とは何かというと、「一つの材料を、めちゃくちゃ小さなブロックの集まり」といったものです。
材料力学の入門レベルで学習するようなシンプルな問題であれば、先程の「仮想断面」が理解できていればある程度解くことができます。
ところが、材料力学の問題が複雑になってくると、これだけでは問題を解くことができません

場所によって内力の大きさや向きが違う、断面積が変化するなどといった問題がそうですね。穴のあいた材料に荷重をかけたケースや、ダビデ像のような複雑形状のものに荷重をかけたケースなどがあります笑。
そこで便利な考え方が、めちゃくちゃ小さなブロック(微小要素)の集まりとするやり方です。
小さなブロックに区切ることで、場所によって内力の大きさや向きが異なっていても、断面積が変化する場合でも、ブロックごとに考えることで対応することができます。
以下に、実際に解析ソフトで計算させてみた例を示します。微小要素というものの雰囲気だけ掴んでいただければ幸いです。
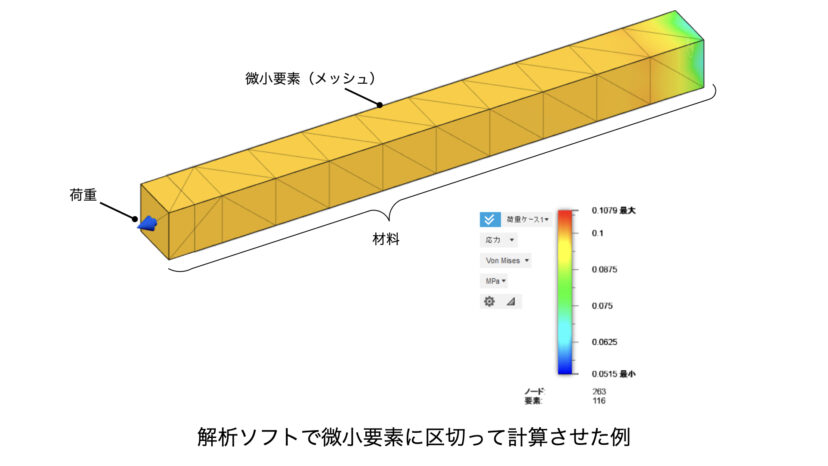
この図では三角形の形に区切っていますが、材料力学の教科書などでは四角形に区切っていることがほとんどです(ソフトでそのような設定ができないので許してください・・・)。
材料の左の方はオレンジとなっており応力が高く出ていますが、材料の右側では黄色や緑となっており、応力は若干低めです。
このように微小要素を活用することで、仮想断面ではできないような詳細な計算が可能となります。

実際に微小要素のサイズをどれぐらい小さくするかは、「問題の複雑さ」や「要求される計算精度」によります。場合によっては、解析ソフトを使わないと計算が難しいですし、パソコンでさえ計算に数時間かかるケースもあります。
学校のテストなど、応力を手計算で計算をするなら、仮想断面で考える方が圧倒的に多いです。
ですが、学校のテスト対策等であれば、これから出てくる材料力学の公式の導出等を理解するために、微小要素の考え方も覚えておく必要があります。
垂直応力とせん断応力の違いはズバリ、仮想断面や微小要素の「面」に対しての応力の向きです。
荷重や内力といった「力」がベクトル量であるように、「応力」もまたベクトル量です。
これを踏まえて、仮想断面や微小要素の面に対して垂直方向にかかる応力を「垂直応力」といいます。
垂直応力は一般的にσ(シグマ)と表します。
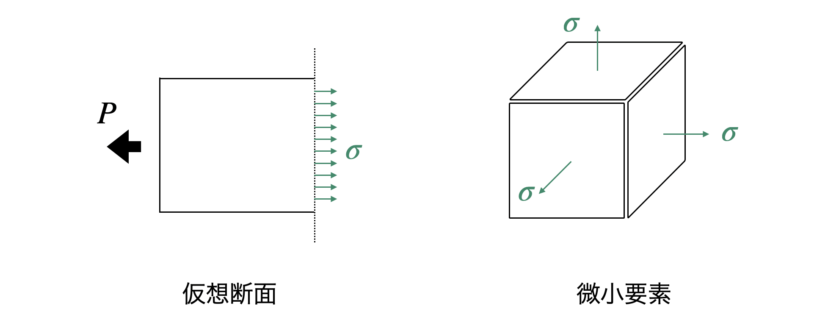
そして、仮想断面や微小要素の面に対して垂直方向にかかる応力を「せん断応力」といいます。
せん断応力は一般的にτ(タウ)と表します。
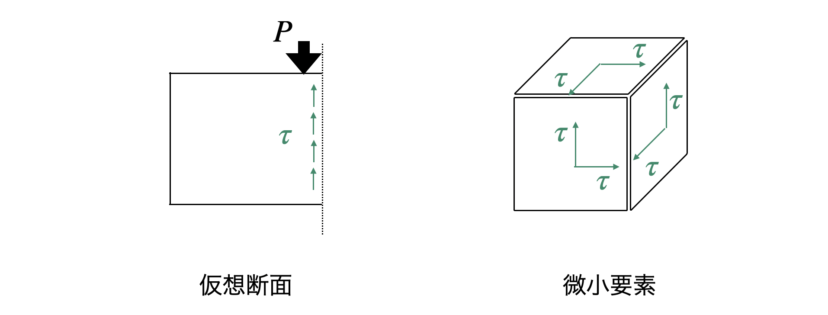

ちなみに、麺に対して斜めに応力がかかっている場合は、その応力を「面に対して垂直な成分」と「面に対して平行な成分」とにベクトル分解をして考えます。
5種類の各荷重と、それによって発生する各応力についてですが、いずれも「垂直応力」と「せん断応力」の2種類だけを使って表現することができます。
これについてまとめたのが、下の表です。
| 名称 | 応力の構成 | 説明 | 図 | 公式 |
| 引張応力 | 垂直応力 | – | 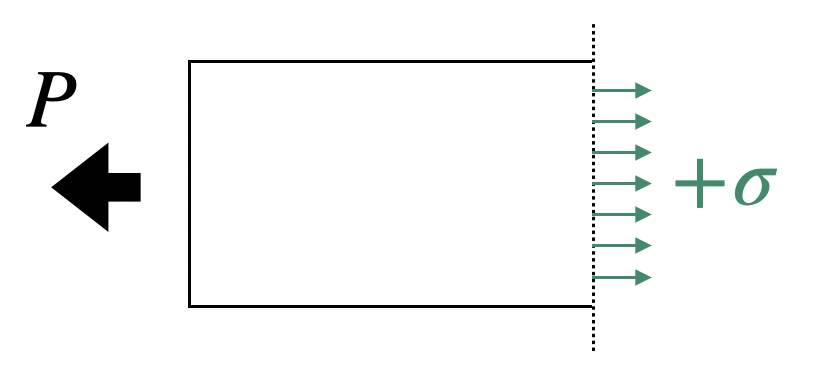 |
$$\sigma =\frac{F}{A}$$ |
| 圧縮応力 | 垂直応力 | – | 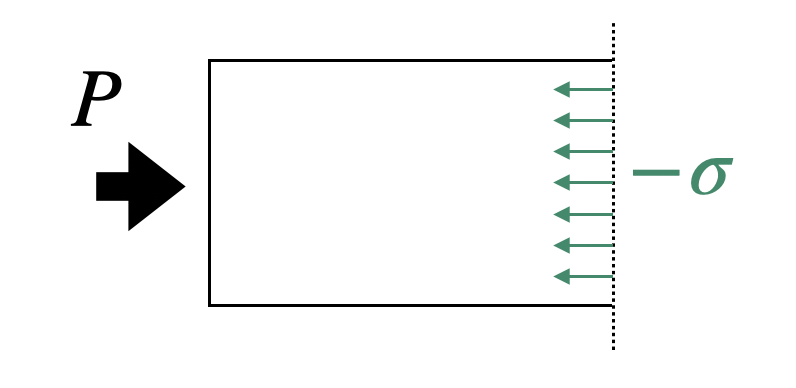 |
$$\sigma =\frac{F}{A}$$ |
| せん断応力 | せん断応力 | – | 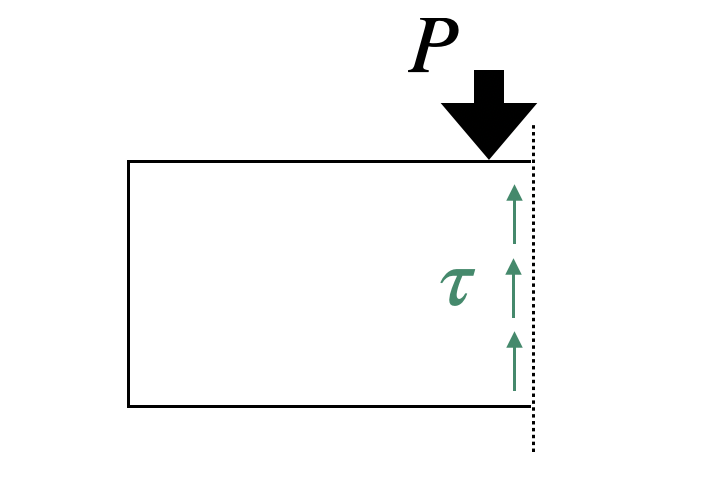 |
$$\tau=\frac{F}{A}$$ |
| 曲げ応力 | 垂直応力 (+せん断応力) |
せん断応力は、垂直応力と比較して微小なため考慮しないことが多い。断面内で応力の大きさや向きがバラバラなので、公式が若干複雑。 |  |
$$\sigma_M=\frac{M}{Z}$$ |
| ねじりせん断応力 | せん断応力 | 円周方向のせん断応力と考える。断面内で応力の大きさや向きがバラバラなので、公式が若干複雑。 | 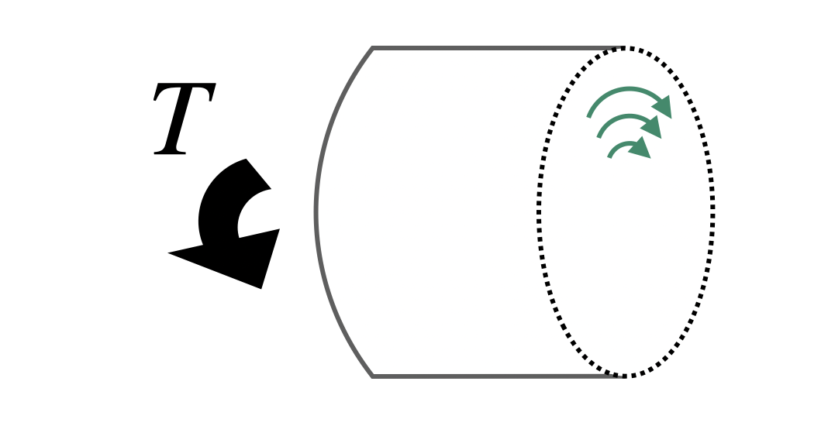 |
$$\tau=\frac{T}{Z_p}$$ |
公式についてはここでは覚える必要はありませんし、詳細は別ベージにて説明をします。
ここでは「へぇー」という雰囲気だけ掴んでいただければOKです。
今回の内容についてまとめると、以下の通りとなります。
今回は以上となります。ご一読、ありがとうございました。
続きはこちら▼
高校の数学とか物理とかめちゃくちゃ苦手なレベルな人向け書籍▼
高校の数学・物理はある程度できる人向け書籍▼
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


【材料力学で一番大事】応力とひずみについて解説
材料力学 演習問題 01【応力】
