曲げ応力の考え方の土台は、中立軸

今回は、梁の曲げ応力の求め方を解説するにあたって重要な、「中立軸」の話をします。

例えば、以下のような曲げ荷重がかかった梁を見てみると、梁は曲線を描くように変形します。

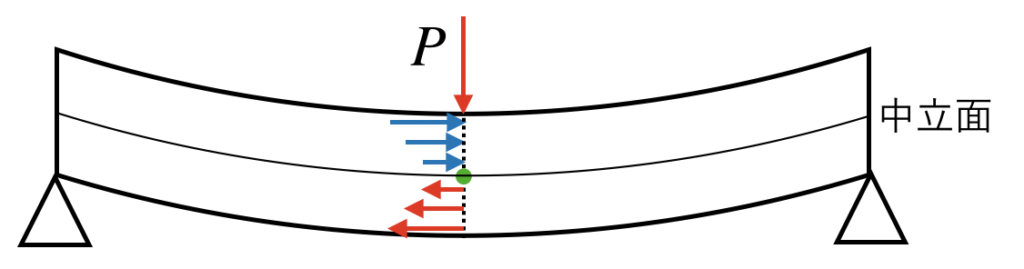
この曲線の内側では圧縮荷重（青い矢印）が、
外側では引張荷重（赤い矢印）がかかっており、

その荷重の大きさは、それぞれ内側・外側にいくほど大きくなります。

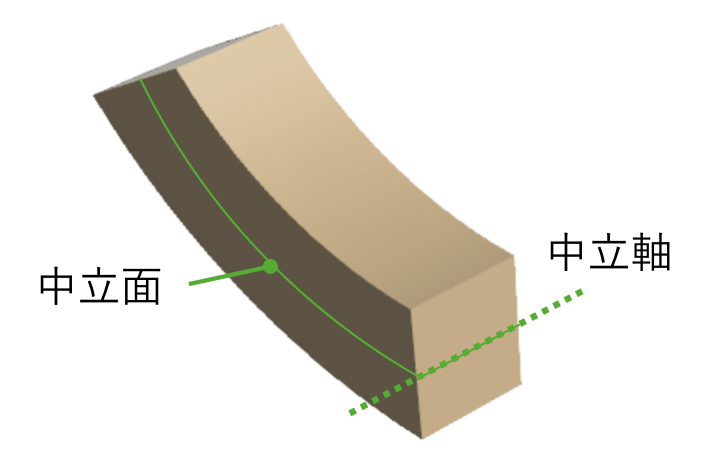
逆に、梁の中央付近には、圧縮も引張も荷重がかからない面があり、このことを「中立面」と呼びます。

そしてお馴染みどおり、仮想的に切り離してみたときに、
仮想断面上の、中立面と交わる線のことを「中立軸」と呼びます。

この「中立軸」の存在は、曲げ応力の考え方や公式を導出する上で、土台となっているほど重要となります。

ということで、今回はこの「中立軸」について、お話ししていきます。

中立軸って、具体的にどこ？

中立軸の定義は「梁において、仮想断面上で、内力が0の面（中立面）を通る線」のことを言います。

では、具体的にその線の場所はどこか？

今、梁に軸力（梁の長手方向にかかる荷重）がないとすると、
以下の2つの条件を満たす線が中立軸となります。

• 曲げ変形をした際の、奥行き方向であること
• 梁の仮想断面の図心を通ること

ただし、この理由については今回省略します（積分の知識が必要なので）。

梁の奥行き方向

これは、正式な呼び方ではなく、私がつけた呼び方です。

「梁の奥行き方向」とは、梁を二次元でモデル化したときの、紙面方向（紙に垂直な方向）です。

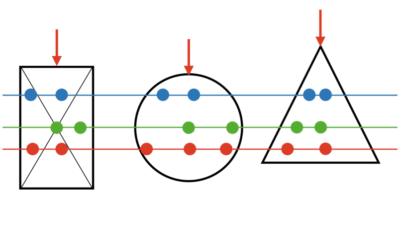
言葉だと難しいですが、以下図の緑色の方向です。

仮想断面の図心

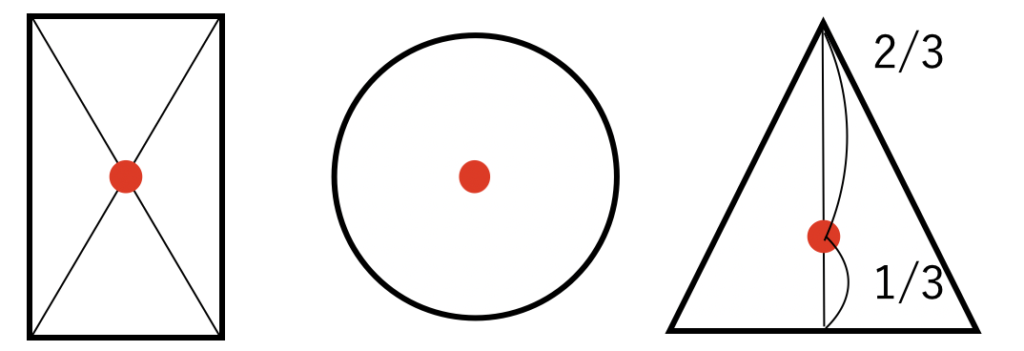
図心とは、重心とほぼ同じ意味です。

重心に糸をくくりつけて吊るすと、
その物体は回転することなく、その姿勢を保ち続けようとします。

重心の位置は図形によって異なり、例えば、

• 断面が長方形の梁の場合は、対角線の交点
• 断面が円の場合は、円の中心
• 断面が三角形の場合は、頂点と対辺の中点とを結んだ線を、頂点から1：2に内分する位置

となります。

これらの点を通り、かつ円周方向の面なので、例えば長方形断面の場合で、下の図のように変形すれば、中立面は緑色の部分になります。

また、下の図のように変形する方向が90度変われば、中立面も90度変わります。

[mathjax]$$\begin{align}L=\rho \theta\varepsilon=\frac{(\rho+y)\\end{align}$$

梁が軸力を受けると、中立軸は移動する

もう一度中立軸の定義をあげますと「梁において、仮想断面上で、内力が0の面（中立面）を通る線」のことをいうのでした。

そのため、梁が軸力を受けると、仮想断面上で、内力が0となる面の位置は、当然移動します。

以下の図を見比べてみましょう。

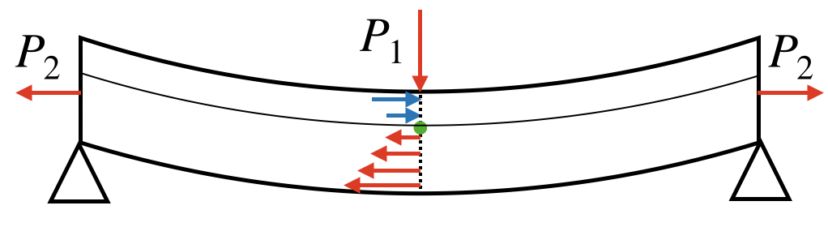
理由は簡単で「曲げによって発生する応力」に「引張によって発生する応力」を足し算したからです。

よって、もともと中立軸の位置だったところは「引張によって発生した応力」が足された分、引張り応力となります。

一方で、圧縮応力はマイナスであるため、「引張によって発生した応力」と相殺されたところが、新しい中立軸の位置となります。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...