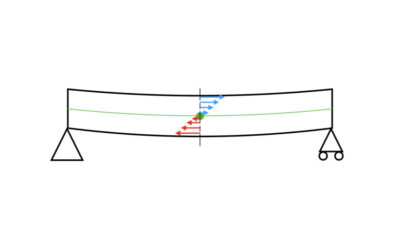
応力を求めるためのアプローチ方法には、主に2通りあります。
一つは、前回やったように、変形量・ひずみから考えていき、フックの法則を使って求める方法です。
このアプローチから、以下の式が得られました。
[mathjax]
$$\begin{align}
\sigma=E\varepsilon=E\frac{y}{r}\cdots(1)
\end{align}$$
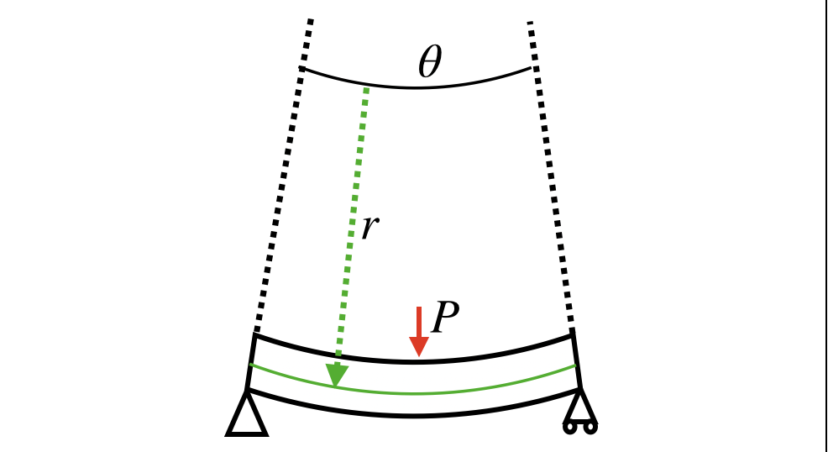
ここで、rは曲率半径と呼ばれるものです。
ただし、設計においては曲率半径がわかっているケースはほとんどありません。
そもそも、この曲率半径は、何によって決まるのか?
結論から言うと、材料にかかる荷重や、材料の断面形状などによって決まります。
今回はこのことを解き明かすために、
曲げによる応力を、「応力の定義」からアプローチをするという方法でお話ししていきます。
梁の曲げ問題では、せん断力と曲げモーメントが内力としてかかりますが、
せん断力によって発生する応力は、曲げモーメントによって発生する応力よりも影響が少ないことがほとんどであるため、
ここでは、曲げモーメントについて考えます。
応力は「内力」を「仮想断面の面積」で割ったものです。
これは裏を返すと、「仮想断面上の応力を全て足すと、内力になる」と言うことです。
これをモーメントについて置き換えると、
梁の曲げによって発生した「材料内部の曲げモーメント」は、
「仮想断面上で発生するある場所での応力σ」と「その点と中立面(中立軸)との距離y」とを掛け算したモーメントを求め、これを「仮想断面上の全ての場所について足し合わせたもの」となります。
$$
M=\sigma_1y_1\times n_1+\sigma_2y_2\times n_2+\cdots\quad \cdots(2)
$$
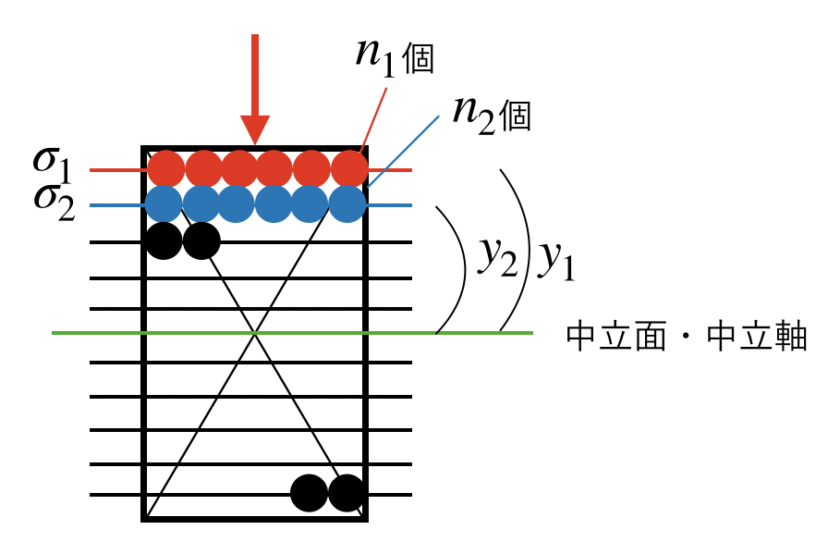
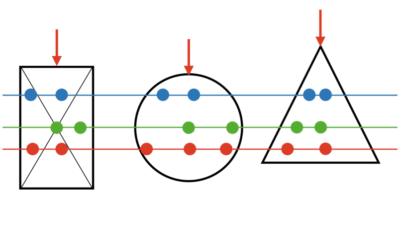
イメージは上の図ですが、この一つ一つの丸が応力の発生している場所を表します。
この領域を小さくすればするほど、計算の精度が上がります。
「画素数が増えるほど、写真がキレイに映る」ような感じです。
ここで、各場所の応力は、(1)式を使って置き換えることができます。
例えば、中立面(中立軸)からy1だけはなれた場所で発生する応力は、(1)式を使うと、次のようになります。
$$\sigma_1=E\frac{y_1}{r}$$
すると、(2)式は次のように表すことができます。
$$
M=\frac{E}{r}(y_1^2\times n_1+y_2^2\times n_2+\cdots)\quad\cdots(3)
$$
さて、この(3)式ですが、なんだか、( )の中身が気持ち悪いですね。
ですが、このカッコの中身は「断面二次モーメント」という名前で呼ばれており、記号はIて表されます。
よって、(3)式を書き換えると、今回求めたかった曲率半径rは次のように表すことができます。
$$
M=\frac{EI}{r}\\
\frac{1}{r}=\frac{M}{EI} \cdots(4)
$$
この(4)式は、曲率半径と曲げ荷重との関係に橋をかける、非常に重要な式となります。
ちなみに、後に代入をしやすくするためにrではなく1/rという形で表しておりますが、
この半径の逆数は「曲率」という名前がついております。
名前がついているからといって、特に難しいわけではなく、
単純に「曲率が大きいほど、カーブがきつい」と言う意味になります。
例えば、表面張力を計算する時などに、曲率が登場したりしますね。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

曲げ荷重によるひずみ方は、中立面からの距離に依存する
曲げ応力の導出と計算式を解説【断面係数が必要】