断面二次モーメントって、どんな意味か？についての解説

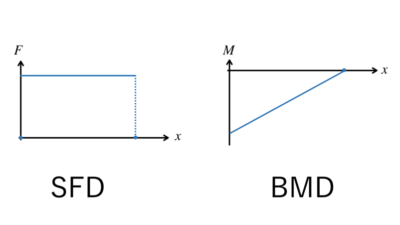
曲げモーメントを、応力の定義からアプローチしたときに、
断面二次モーメントIを定義することによって、測定が難しい梁の曲率半径は以下のように表せます。

$$\frac{1}{r}=\frac{M}{EI}\cdots(1)$$

ここで、断面二次モーメントはどのように定義されたかと言うと、以下のように置き換えたのでした。

$$I=y_1^2\times n_1+y_2^2\times n_2+\cdots \quad \cdots(2)$$

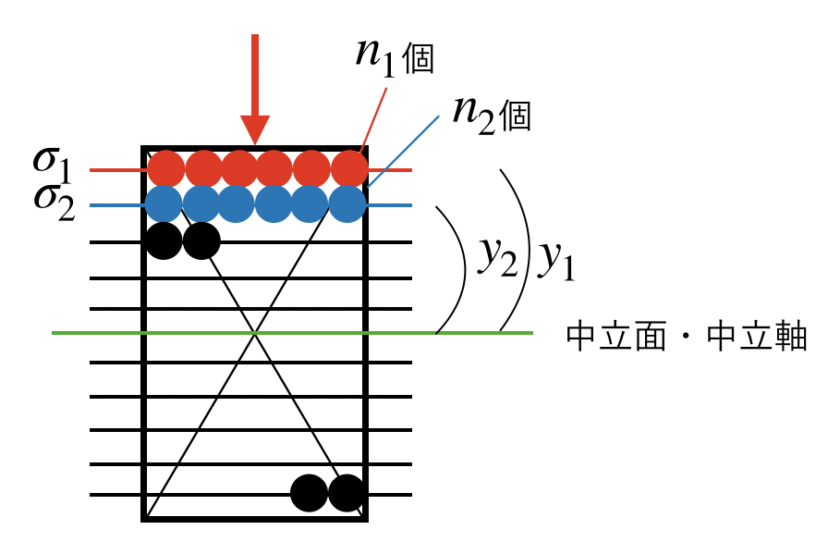
では、そもそもこの断面二次モーメントとはなんなのか？

面倒くさい無数の足し算の部分を、とりあえずIで置き換えていますが、

このIが計算可能な値であることがわかっていないと、文字で置き換えをしても意味がありません。

今回はこの断面二次モーメントについて深掘りして、お話ししていきます。

面倒くさい部分について、面倒臭がらずに考えてみよう

$$I=y_1^2\times n_1+y_2^2\times n_2+\cdots \quad \cdots(2)$$

さて、これはどのような計算をしているかを、少しずつ見ていきましょう。

まず「y」は中立面(中立軸)からの距離、つまり梁の高さ方向を表しております。

その「y」に2乗がかかっておりますことから、梁の高さが高いほど、断面二次モーメントが大きくなります。

次にnですが、これは梁の奥行き方向を表しております。

よって、梁の幅が広いほど、断面二次モーメントが大きくなりますが、高さ方向ほどは増加はしません。

このことから、なるべく重量を増やさずに、断面二次モーメントを効率的に増やそうと思ったら、梁の高さを増やすのが最適であるということになります。

断面二次モーメントの意味を理解するには、冒頭で述べた以下の式を見ればよくわかります。

$$\frac{1}{r}=\frac{M}{EI}\cdots(1)$$

この式をみると、断面二次モーメントが大きくなるほど、曲率半径が大きくなります。(曲率でいうと、小さくなります)

つまり、断面二次モーメントが大きいということは、梁に荷重がかかったときの変形のカーブが緩やかになることを意味します。

断面二次モーメントは、梁の断面に関する多数の足し算が、定義です。
そして単位は、[mm⁴]です。

しかし、定義だけを見ても、断面二次モーメントの意味が、学生当時の私なんかは、さっぱり分かりませんでした。

(1)式は重要な式であると前回申し上げましたが、この断面二次モーメントの意味を理解する上でも非常に役に立ちます。

仮想断面における応力の発生場所を細かく分ければ分けるほど、計算の精度が上がります。

しかし、その調子で精度をどんどん上げていっても、Iは無限に増加をするわけではなく、ある一つの値に近づいていきます(ある値に近づいていくことを、数学では収束と言います)。

では、一体どんな値に近づくのか？

それは、梁の断面の形によって決まります。

これを根本から理解しようとすると、積分の知識が必要となるので今回は省略しますが、

ものづくりでよく使われているような梁では、以下のような値に近づくことがわかっております。

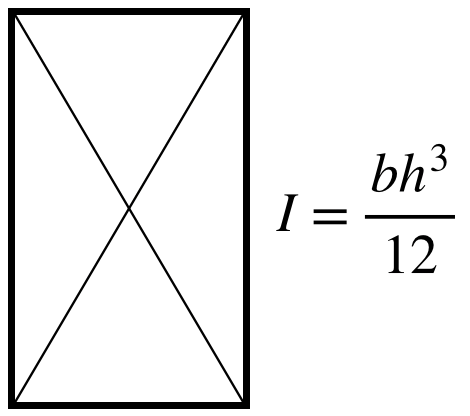
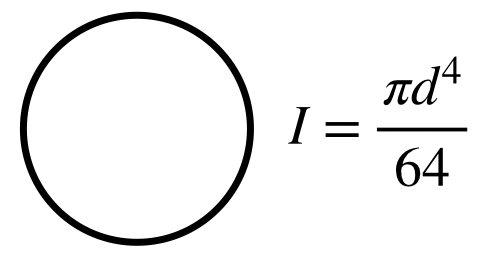
断面二次モーメント的に理にかなった形状といえば、建物の鉄骨などに使われている、H鋼が有名です。

先ほど、重量を増やさずに、効率的に増やそうと思ったら、梁の高さを増やすのが適切だと言いましたが、

さらに軽くて丈夫にしようと思ったら、図心近くの断面を削るのが理にかなっています。

なぜなら、中立面（中立軸）から近い場所は、断面二次モーメントの増加に、あまり貢献しないからです。

そうすると、鉄鋼で使われているような、H鋼の形が理にかなっているということができます。