今回は、引張荷重を受ける材料変形量を、微小要素の考えを導入して求めていきたいと思います。
断面形状が変わらない材料の場合は、仮想的に切り離して釣り合いの式を立てることで簡単に求めることができます。
一方で、断面形状が変わる材料の場合の変形量は、これを仮想的に切り離す方法では求めることが困難です。
【問題】
以下のように直径がD1からD2に一様に変化する、長さLの丸棒のD1側が壁に固定されています。D2側を力Pで引張った時に、棒はどの程度伸びるか求めてください。ただし、ヤング率はEとします。
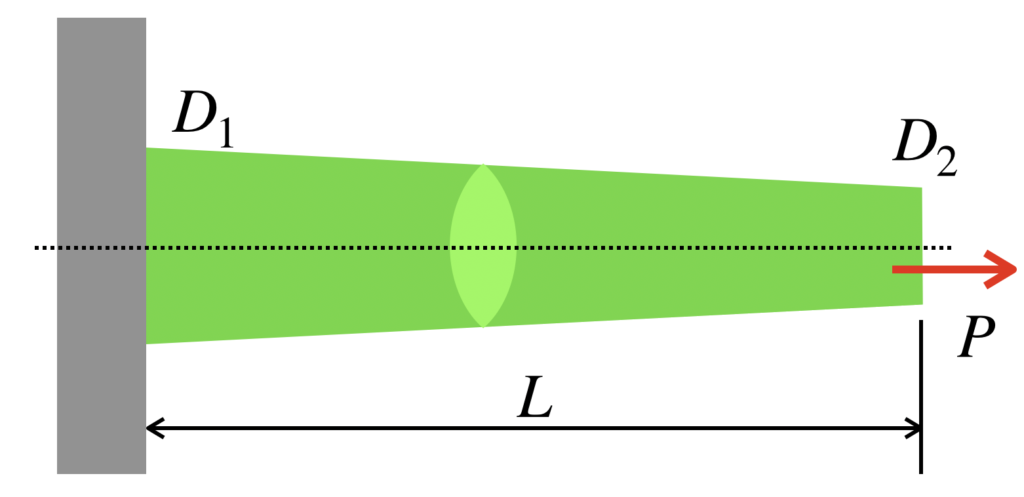
このような、少し難易度が上がった問題について、今回はお話しします。
以下のように、壁の位置を原点として、長手方向にx軸を設定します。
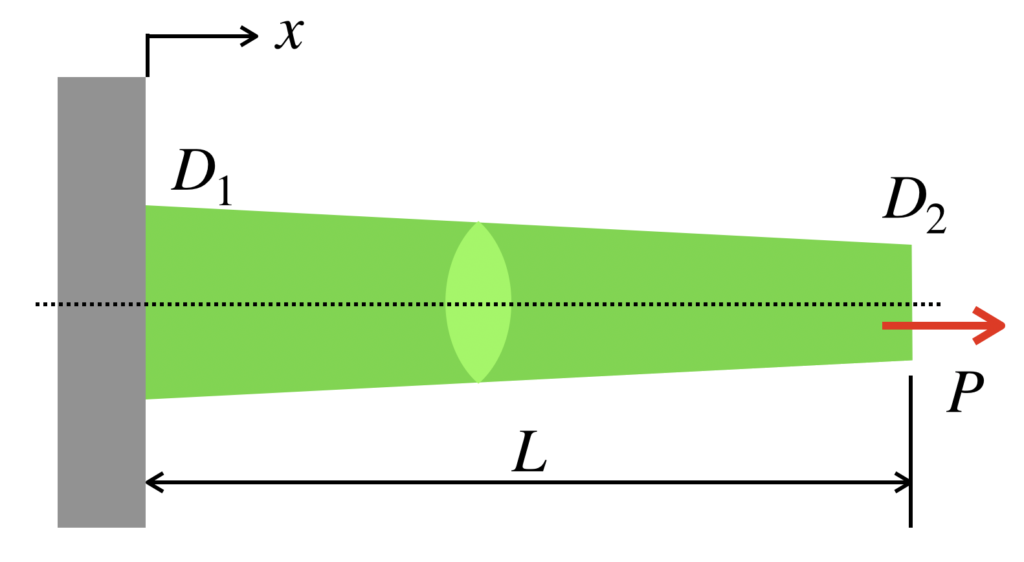
ここで、x=xの位置と、x=x+dxの位置に囲まれた微小要素の伸びについて考えてみます。
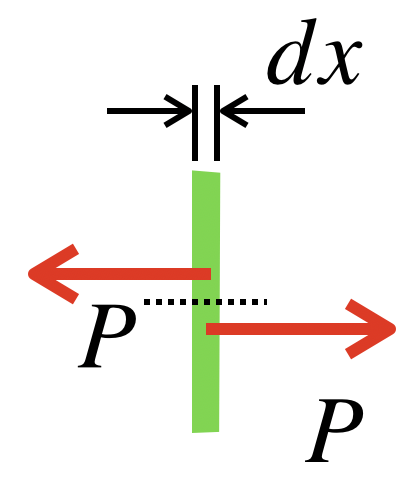
とりあえず、x=xの位置における断面積をA(x)とするとなります。((x)はf(x)と同じように、「xの関数である」という意味です)
$$A(x)=\frac{\pi}{4}(\frac{D_2-D_1}{L}x+D_1)^2\cdots(1)$$
続いて、この微小要素の伸びをdlとしますと、以下のようになります。
$$dl=\varepsilon dx\cdots(2)$$
ひずみと変形量の関係
$$\varepsilon=\frac{\Delta L}{L}\rightarrow \Delta L=\varepsilon L$$
さらに、フックの法則や応力の定義を使うと、(2)式は以下のように変形できます。
$$\begin{align}
dl&=\varepsilon dx\\
&=\frac{\sigma}{E}dx\\
&=\frac{P}{EA(x)}dx\cdots(3)\\
\end{align}$$
フックの法則
$$\sigma=E\varepsilon\rightarrow \varepsilon=\frac{\sigma}{E}$$
荷重と応力の関係
$$\sigma=\frac{P}{A}$$
(3)式に、(1)式を代入しますと、以下のようになります。
$$\begin{align}
dl&=\frac{P}{EA(x)}dx\\
&=\frac{P}{E}\frac{4}{\pi}\frac{1}{(((D_2-D_1)x)/L+D_1)^2}dx\cdots(4)
\end{align}$$
(4)式が微小要素に発生する変形量となります。問題で問われているのは、棒全体の変形量なので、(4)式をx=0からx=Lまで積分をします。
ここで、棒全体の変形量をΔLとしますと、
$$\begin{align}
\Delta L&=\int^{L}_{0}\frac{P}{E}\frac{4}{\pi}\frac{1}{(((D_2-D_1)x)/L+D_1)^2}dx\\
&=\frac{4P}{\pi E}\int^{L}_{0}(\frac{D_2-D_1}{L}x+D_1)^{-2}\\
&=\frac{4P}{\pi E}[(\frac{1}{-1})(\frac{L}{D_2-D_1})(\frac{D_2-D_1}{L}x+D_1)^{-1}]^L_0\\
&=\frac{4PL}{\pi E(D_1-D_2)}(\frac{1}{D_2}-\frac{1}{D_1})\\
&=\frac{4PL}{\pi E(D_1-D_2)}\frac{D_1-D_2}{D_1D_2}\\
&=\frac{4PL}{\pi E(D_1D_2)}\\
\end{align}$$
積分の公式
$$\int^{x_2}_{x_1}(ax+b)^n=[\frac{1}{n+1}\frac{1}{a}(ax+b)^{n+1}]^{x_2}_{x_1}$$
ただしn≠-1
これが答えとなります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

【まとめ】材料力学の応力の計算方法のロードマップ
遠心力を受ける物体の伸びの計算方法【材料力学】