こんにちは!リヴィです。
今回は、締付けトルクと軸力の関係式の導出についての第2回目です。
前回、必要となる締付けトルクは、以下の2つに分けて考えることができると説明をしました。
$$T=T_s+T_w$$
| $$T$$ | 締付けトルク |
| $$T_s$$ | ねじ面で必要な締付けトルク |
| $$T_w$$ | 座面で必要な締付けトルク |
このうち、今回は「ねじ面で必要な締付けトルク」に着目して、解説をしていきます。
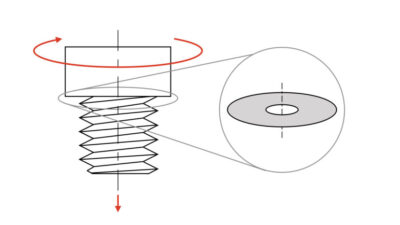
では早速ねじ面の力関係について解説をしたいところなのですが、一般的に使われる三角ねじの話は一旦おいておいて、まずはねじ山が長方形の形をしている「四角ねじ」について解説をします。
というのも、いきなり三角ねじについて考えるよりも、四角ねじの力の関係について理解してからの方が、難易度がぜんぜん違うためです。

三角ねじの話をいきなり始めると、sinやらcosやらがごちゃごちゃしているので、ハードルが高くなります。
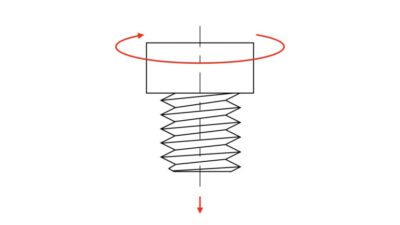
以下の図のように、ボルトまたはナットを締付けてたときに発生した軸力と、それに必要な締付けトルクについて考えていきます。
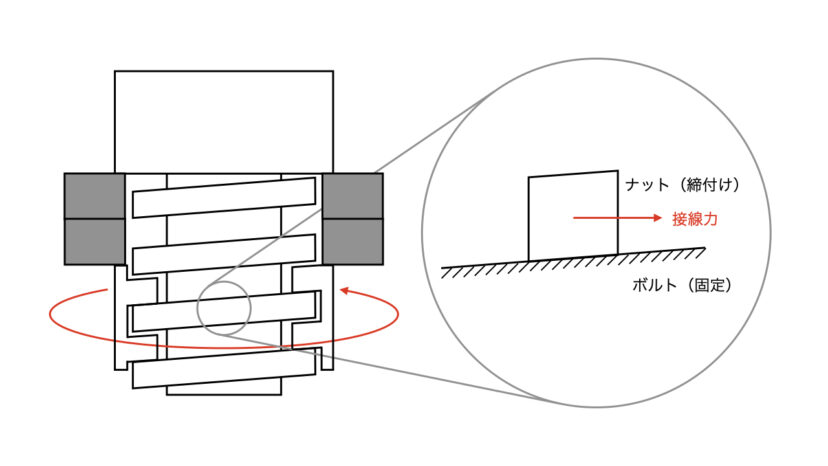
ここで締付けトルクについてなのですが、締付けトルクという「回転の力」と、軸力という「直線の力」のように、種類の違うものを同時に取り扱うのは煩わしいです。
そこで、以下の式を使って、締付けトルクではなく、接線力という直線の力を使って、ねじの力関係を解説していきまs。
$$T_s=F_s\cdot \frac{d_2}{2}\cdots(1-1)$$
| $$T_s$$ | ねじ面で必要な締付けトルク |
| $$F_s$$ | 接線力 |
| $$d_2$$ | 有効径 |

接線力は、おねじ・めねじの噛合い面全体を考える必要はなく、有効径の位置で接線力を発生させるとみなします。
では、接線力と軸力を使って、ねじ面の力関係に焦点を当てて、考えてみましょう。
ねじ面の力は、以下の図のようなものが発生しています。

よって、とある軸力Faを発生させるために必要な接線力Tsは以下の通りとなります。
$$\begin{cases}
N-F_a\cos\beta-F_s\sin\beta&=0\cdots(1-2)\\
F_s\cos\beta-f_s-F_a\sin\beta&=0\cdots(1-3)\\
f_s=\mu_s N\cdots(1-4)
\end{cases}$$
| $$N$$ | 垂直抗力 |
| $$F_a$ | 軸力 |
| $$F_s$$ | 接線力 |
| $$\beta$$ | リード角 |
| $$\f_s$$ | ねじ面の摩擦力 |
| $$\mu_s$$ | 摩擦係数 |
これらの式を解くと、以下の式が得られます。
$$\begin{cases}
N&=F_a\cos\beta+F_s\sin\beta\\
f_s&=F_s\cos\beta-F_a\sin\beta
\end{cases}$$
これらの式を(1-4)式に代入すると、以下のようになります。
$$F_a\sin\beta-F_s\cos\beta=\mu_s(F_a\cos\beta+F_s\sin\beta)\cdots(1-5)$$
ここで、摩擦係数μsを摩擦角ρを使って表現します。
$$\begin{cases}
\mu_s=\tan\rho\cdots(1-6)
\end{cases}$$

ここの考え方がわからないという人は、第一回の摩擦角の説明を御覧ください。
これを(1-5)式に代入します。
$$F_s\cos\beta-F_a\sin\beta=\tan\rho(F_a\cos\beta+F_s\sin\beta)$$
ここで、三角関数の公式より、tanをsinとcosを使って表します。
ポイント
$$\tan\rho=\frac{\sin\rho}{\cos\rho}$$
$$F_s\cos\beta-F_a\sin\beta=\frac{\sin\rho}{\cos\rho}(F_a\cos\beta+F_s\sin\beta)$$
$$F_s\cos\beta\cos\rho-F_s\sin\beta\sin\rho=F_a\sin\beta\cos\rho+F_a\cos\beta\sin\rho$$
$$F_s(\cos\beta\cos\rho-\sin\beta\sin\rho)=F_a(\sin\beta\cos\rho+\cos\beta\sin\rho)$$
ここで、加法定理を使います。
ポイント
$$\cos\beta\cos\rho-\sin\beta\sin\rho=\cos(\beta+\rho)\\
\sin\beta\cos\rho+\cos\beta\sin\rho=\sin(\beta+\rho)$$
これを使って、さらに式を整理していきます。
$$F_s\cos(\beta+\rho)=F_a\sin(\beta+\rho)$$
$$F_s=F_a\frac{\sin(\beta+\rho)}{\cos(\beta+\rho)}$$
ここで、三角関数の公式より、今度はsinとcosを、tanを使って表します。
ポイント
$$\frac{\sin(\beta+\rho)}{\cos(\beta+\rho)}=\tan(\beta+\rho)$$
よって、四角ねじのねじ面の力関係は、
$$F_s=F_a\tan(\beta+\rho)$$
となります。
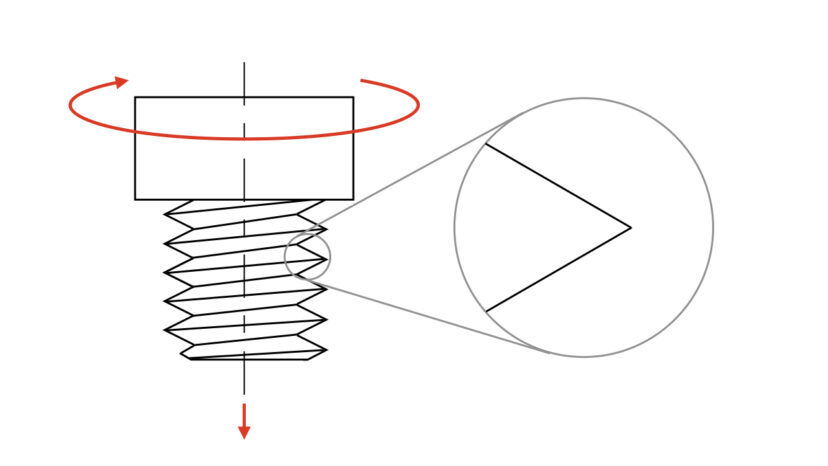
ではここから、三角ねじのねじ面の力関係について解説していきます。
三角ねじの関連の資料を正確に読み解くためには「どの座標系で議論されているか?」をしっかり把握しながら読み進めることが、非常に重要となっていきます。
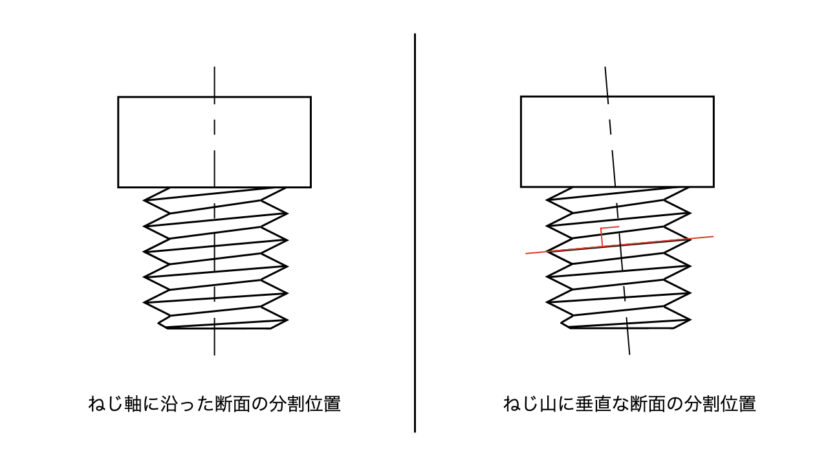
ねじ関連の資料で登場する座標というのは「ねじ軸に沿った座標」と「ねじ山に垂直な座標」です。
例えば、第一回の記事で「ねじ断面が正三角形に近い形状となっているねじ」と解説しましたが、これはどちらの座標系で議論されたものでしょうか?
正解は前者の「ねじ軸に沿った座標」です。
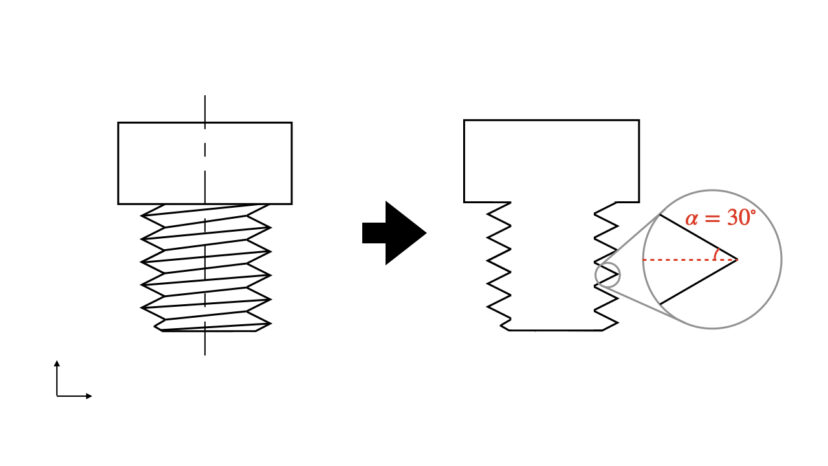
ところが、ねじの力関係について議論をするためには、「ねじ山に垂直な座標」で考える必要があります。
なぜなら、ねじに発生する力について考えるベクトルが、ねじのリード角分だけ傾いたいるからです。
そのため、ねじ山に垂直な座標で断面を切ったねじ山を見ると、実は正三角形ではなく、二等辺三角形になります。
こういったように、どの座標系で議論されているかでややこしくなるので、前者のねじ軸に沿った座標で見たねじ山の半角と区別して、後者のねじ山に垂直な座標で断面を切ったねじ山の半角はα’という記号がよく使われます。
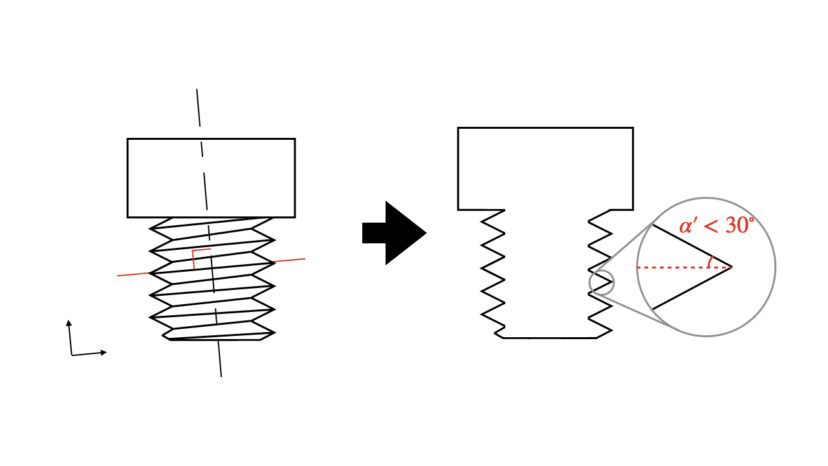
三角ねじの力の関係式についてですが、「垂直抗力」および「摩擦力」の観点から、四角ねじと三角ねじとで異なってきます。
三角ねじのねじ面は、ねじ山の角度分だけ傾いているので、それを考慮する必要があるのです。
つまり、「四角ねじの場合の垂直抗力」を「三角ねじのねじ山の半角分だけ傾いた方向」に直せばいいということになります。
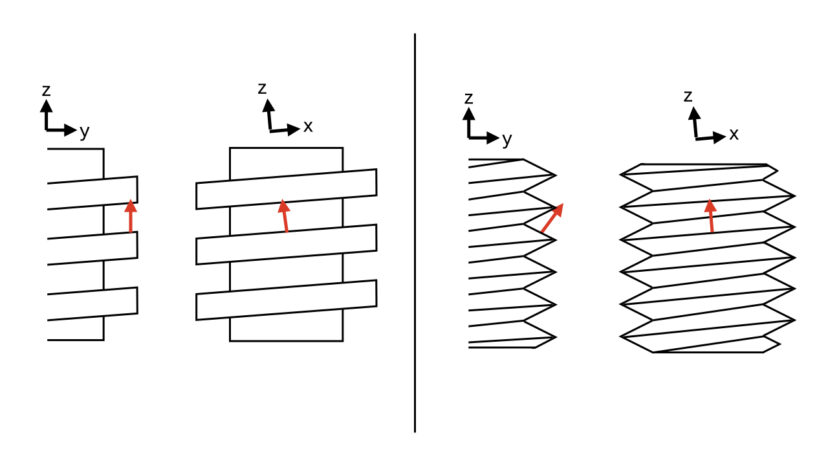

「四角ねじのねじ山の半角は0°」と解釈することもできます。
ではボルトまたはナットを締付けてたときに発生した軸力と、それに必要な締付けトルクについて考えていきます。
ねじ面に垂直な方向と、ねじ面に平行な方向についてそれぞれ式を立てると、以下の通りとなります。
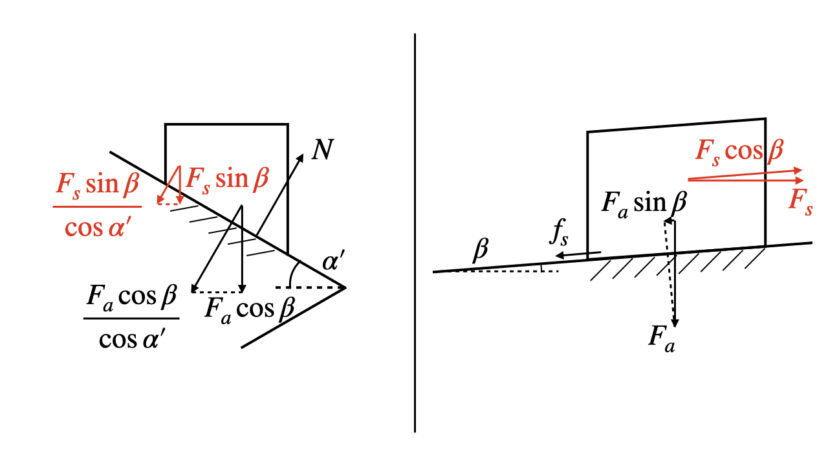
$$\begin{cases}
N-\displaystyle\frac{F_a\cos\beta}{\cos\alpha’}-\frac{F_s\sin\beta}{\cos\alpha’}&=0 &\cdots(2-1)\\
F_s\cos\beta-f_s-F_a\sin\beta&=0 &\cdots(2-2)\\
f_s&=\mu_s N&\cdots(2-3)
\end{cases}$$
| $$N$$ | 垂直抗力 |
| $$F_a$$ | 軸力 |
| $$F_s$$ | 接線力 |
| $$\beta$$ | リード角 |
| $$\alpha’$$ | ねじ山に垂直な断面で切ったときの、ねじ山の半角 |
| $$\mu_s$$ | ねじ面の静止摩擦力 |

この式がわからない場合は、詳しい解説を後述していますので、ご参照ください。
(2-1)、(2-2)により、
$$N=\displaystyle\frac{F_a\cos\beta}{\cos\alpha’}+\frac{F_s\sin\beta}{\cos\alpha’}\\
f_s=F_a\sin\beta-F_s\cos\beta$$
これらを(2-3)に代入すると以下の通りとなります。
$$F_a\sin\beta-F_s\cos\beta=\mu_s(\displaystyle\frac{F_a\cos\beta}{\cos\alpha’}+\frac{F_s\sin\beta}{\cos\alpha’})\cdots(2-4)$$
ここで摩擦角を導入していきますが、今回は以下のように置き換えます。
$$\mu_s=\frac{\tan\rho}{\cos\alpha’}=\tan\rho’ \cdots(2-5)$$
(2-5)式を(2-4)式に代入すると、以下の通りとなります。
$$F_a\sin\beta-F_s\cos\beta=F_a\cos\beta\tan\rho’+F_s\sin\beta\tan\rho’\cdots(2-6)$$
ここまでくれば、四角ねじの力関係と同様にして、以下のような式に整理することができます。
$$F_s=F_a\tan(\beta+\rho’)\cdots(2-7)$$
(2-7)式について、近似を使ってもうひと工夫していきます。
まずは、tanの部分について加法定理を適用させていきます。
tanの加法定理
$$\tan(\rho’+\beta)=\frac{\tan\rho’+\tan\beta}{1-\tan\rho’ \tan\beta}$$
これを、(2-7)式に適用すると以下の通りとなります。
$$F_s=F_a\frac{\tan\rho’+\tan\beta}{1-\tan\rho’ \tan\beta} \cdots(3-1)$$
ここで、tanρ’およびtanβのだいたいの値の大きさについて考えてみましょう。
tanρ’は、「摩擦係数」÷「cos α’」です。
$$\tan\rho’=\frac{\tan\rho}{\cos\alpha’}=\frac{\mu_s}{\cos\alpha’} \cdots(2-5)$$
摩擦係数はだいたい0.1~0.2程度、cos α’は固定用ねじの場合でだいたい0.9程度なので、tanρ’の値はだいたい0.1~0.2程度です。
一方でtanβですが、固定用ねじの場合のβは2~4°程度です。
そのため、tanβの値はだいたい0.03~0.05程度となります。
以上のこととから、tanρ’とtanβを使って以下のように近似ができます。
$$\tan\rho’ \tan\beta\simeq0\cdots(3-2)$$
この(3-2)式を、(3-1)式に代入すると、右辺の分母を消去できます。
$$F_s=F_a(\tan\rho’+\tan\beta) \cdots(3-3)$$
これが、三角ねじのねじ面の力関係を表す式となります。

リード角βが小さい「固定用ねじ」だからこそ成立する近似です。並目ねじ・細目ねじなら適用されますが、ハイリードねじ・多条ねじあたりは怪しいので注意です。
(3-3)式は確かに三角ねじ面の力関係を表す式ではありますが、これはねじのリード角が既知のときに使用できる式です。
固定用ねじのリード角は2~4°あたりではあるとはいえ、ねじのサイズによって値がバラバラですし、どれも中途半端な数字なので、少々扱いづらい式です。
そのため、計算をする際には、比較的扱いやすい「リード角を使わないで表現された式」の方を使います。
そうなるように(3-3)式を変換していきます。
まず、ねじの1ピッチ分(1山分)について、らせん状から平面に引き伸ばしたものを考えてみます。
そのときにできる直角三角形について考えてみると、底辺がねじの有効径の円周πD2、高さがピッチP、角度がリード角βと等しくなります。
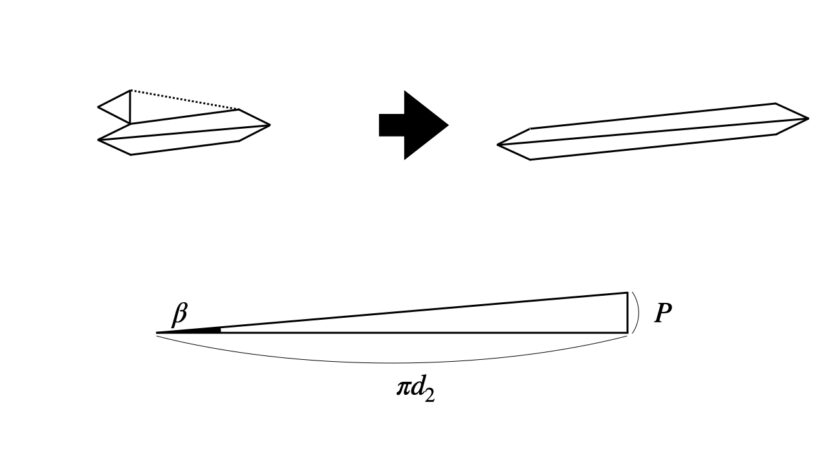
よってリード角βは、tanの定義から以下のように記述することができます。
$$tan\beta=\frac{P}{\pi d_2}\cdots(4-1)$$
| $$\beta$$ | リード角 |
| $$P$$ | ピッチ |
| $$d_2$$ | ねじの有効径 |
この(4-1)式を(3-3)式に代入すると、以下のようになります。
$$F_s=F_a(\tan\rho’+\frac{P}{\pi d_2}) \cdots(4-2)$$
ここで、(1-1)式を使って、接線力を締付けトルクに直すと、
$$\begin{cases}
T_s=F_s\cdot \displaystyle\frac{d_2}{2} \dots(1-1)\\
F_s=F_a(\tan\rho’+\displaystyle\frac{P}{\pi d_2}) \cdots(4-2)
\end{cases}$$
$$\frac{2T_s}{d_2}=F_a(\tan\rho’+\frac{P}{\pi d_2})$$
$$T_s=F_a(\frac{d_2}{2}\tan\rho’+\frac{P}{2\pi})$$
ついでに摩擦角の部分についても、摩擦角を使って式展開することはもうないので、摩擦係数を使った式に直します。
$$T_s=F_a(\frac{d_2}{2}\frac{\mu_s}{\cos\alpha’}+\frac{P}{2\pi})\cdots(4-3)$$
| $$T_s$$ | ねじ面で必要な締付けトルク |
| $$F_a$$ | 軸力 |
| $$d_2$$ | ねじの有効径 |
| $$\mu_s$$ | 摩擦係数 |
| $$\alpha’$$ | ねじ山に垂直な断面で切ったときの、ねじ山の半角 |
| $$P$$ | ねじ山のピッチ |
高い計算精度が必要であれば、この(4-3)式を使います。
ただ、実際に設計で使う程度であれば、そこまでの高精度は必要ないので、以下の近似をします。
$$\alpha’\simeq\alpha$$
| $$\alpha’$$ | ねじ面に垂直な断面で切ったときの、ねじ山の半角 |
| $$\alpha$$ | ねじ軸に沿った断面で切ったときの、ねじ山の半角 |

この近似も、並目ねじ・細目ねじなら適用されますが、ハイリードねじ・多条ねじあたりは怪しいので注意です。
よって(4-3)式にこの近似式を適用すると、ねじ面で必要な締付けトルクと軸力との関係式は以下の通りとなります。
$$T_s=F_a(\frac{d_2}{2}\frac{\mu_s}{\cos\alpha’}+\frac{P}{2\pi})\cdots(4-4)$$
| $$T_s$$ | ねじ面で必要な締付けトルク |
| $$F_a$$ | 軸力 |
| $$d_2$$ | ねじの有効径 |
| $$\mu_s$$ | 摩擦係数 |
| $$\alpha$$ | ねじ軸に沿った断面で切ったときの、ねじ山の半角 |
| $$P$$ | ねじ山のピッチ |
以上が、ねじ面で必要な締付けトルクと軸力の関係式となります。
先ほど示した釣り合いの式を見て、よくわからなかった、いまいち納得がいかない、という人の多くは「cos α’の部分が掛け算ではなく、割り算になっているのが何故なのか?」と思っているのではないでしょうか?
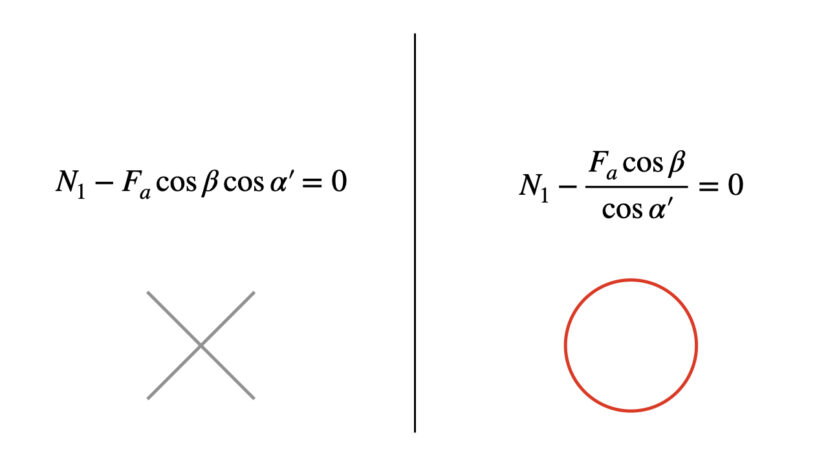
ポイントは「座標のとり方」です。
この部分、非常につまづきやすいので丁寧に解説します。
よくある、「斜面上の物体の摩擦力の問題」と、今回の「ねじ面の摩擦力の問題」とは何が違うのかを、比べてみましょう。
図をシンプルにするために、接線力Fsのベクトルのみ考えていきます。
よくある斜面の問題では、「座標軸に沿っていないベクトル」を「座標軸に沿うように分解する」という方法で解くのが一般的です。
その一方で、今回の三角ねじの問題では「座標軸に沿ったベクトル」を「座標軸に沿っていないベクトル」に分解するものです。
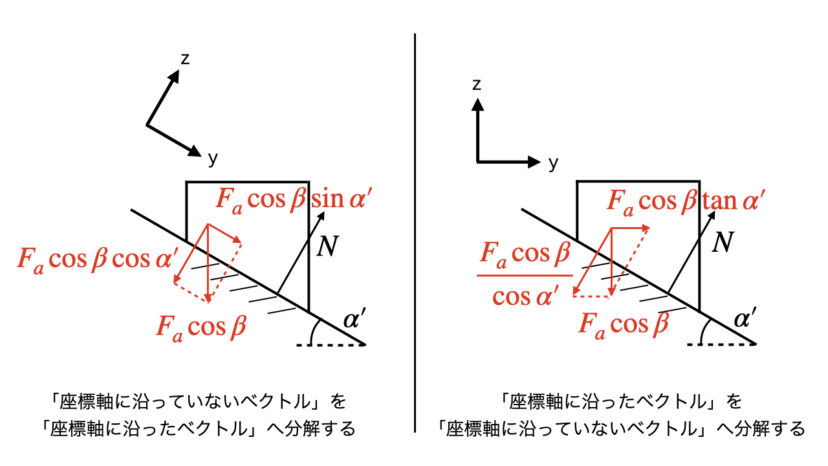
座標軸に沿っていないベクトルに分解するので、cosα’で割るという式になるのです。
ではなぜ、座標軸に沿っていないベクトルに分解するような、複雑なことをするのでしょうか。
それは、分解して出てきたもう一方のベクトルが相殺されて消去できるからです。
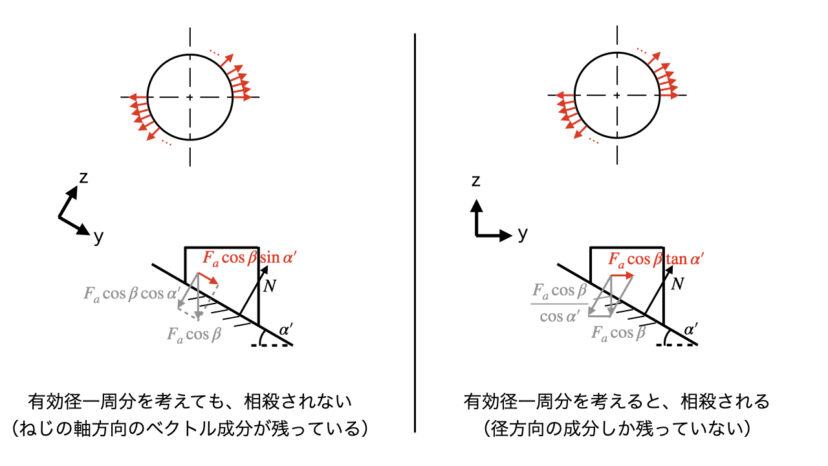
ねじ山の力関係について、有効径一周分を考えて見ましょう。
先程の図の中で、右側のようにベクトルを分解したときに出てくる「Facosβtanα’」ですが、これは有効径一周分を考えると、総和がちょうど0になり、消去されるので、都合が良いのです。
一方で、先程の図の中で、左側のようにベクトルを分解してしまうと、「Facosβsinα’」と釣り合う力が存在しないため、消去できません。
そうなると、この「Facosβsinα’」の力が、ねじ面の力関係に対してどのような影響を及ぼすのかを、さらに考えなければならなくなってくるのです。

有効径一周分を考えるのであれば、厳密に言えば「Fa」ではなく、「Fa/πd2」で考えることになります。ちなみに、接線力についても同様のことが言えます。
今回は、ねじ面の力関係について解説いたしました。
三角関数やら、座標軸の設定やらが難しいですが、ちょっとずつ式を読み解いていただければと思います。
なお余談ですが、今回解説したような「厳密にねじ山が長方形である四角ねじ」は実際にはありません。
というのも、作ろうとしても加工上非常に困難で、どうしても数°程度のテーパが必要になってしまうのです。

最も四角ねじに近いものが、万力やジャッキに使われている「角ねじ」と呼ばれるものですが、やはり若干のテーパがあります。
次回は、「座面で必要な締付けトルク」について、解説していきます。
今回は以上となります。ご一読ありがとうございました。
ねじ関連のおすすめ書籍▼
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

【解説】締め付けトルクと軸力の関係式の導出(1)
【解説】締め付けトルクと軸力の関係式の導出(3)