この記事を読むべき人
ねじは機械の中でもよく使う部品です。
ねじの締め方にはいくつか方法があるのですが、最も一般的なのはトルク法というものです。
これは「軸力とトルクの関係式を使って、ねじを締めたときの軸力から逆算してトルクを求め、そのトルクでねじを締める」という方法です。

トルクレンチを使ってボルト・ナットを締める方法は、まさにこのトルク法に基づいた締結方法ですね。
この、軸力と締め付けトルクとの関係について、結論から言いますと、以下の式のようになります。
$$T=F_a \left (\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+\mu_w \frac{d_w}{2} \right)$$
| $$T$$ | 締付けトルク[N・m] |
| $$F_a$$ | 軸力[N] |
| $$P$$ | ねじのピッチ[mm] |
| $$d_2$$ | ねじの有効径[mm] |
| $$μ_s$$ | ねじ面の滑り摩擦係数[-] |
| $$\alpha$$ | ねじ山の半角[°] |
| $$\mu_w$$ | 座面の滑り摩擦係数[-] |
| $$d_w$$ | 等価摩擦直径[mm] |
よって、主な式の使い方としては、以下の手順となります。
今も昔も、「ねじがクビれた」とか「ねじが破断した」といったトラブルは割と多く、ねじの選定ミスがなかったかとか、ねじ締付時のトルクが合っていたかとかが疑われますが、
この式の裏側にある原理・考え方が理解できていないと、原因究明はなかなか難しいです。
かといって上の式を見ての通り、ねじに関する力学は複雑で、式を見ただけで体が痒くなるという人も多いかと思います。

実際、ベテラン設計者でも、ちゃんと原理がわかっている人は少なく、感覚で選定している人のほうが多いです。まぁ、その感覚が意外と合っていることもありますが笑
そこでこの「締め付けトルクと軸力の関係式の導出」について、なるべくわかりやすく解説していきたいと思います。
ただし、この関係式の導出の話は結構長くなってしまいますので、全部で5回に分けて解説をしていきます。
以下に解説のロードマップを作成いたしましたので、これからこの手順に沿って解説をしていきます。
ねじにかかる力について、ざっくりどのように考えていければ良いのかについて解説していきます。
ねじに関して解説された資料はたくさんあるのですが、「この部分を理解せずに読もうとすると詰みやすいよ」というポイントについて解説いたします。
締付けトルクと軸力の関係式では、右辺の形がごちゃごちゃしていますが、大きく分けて3種類の力が作用していることを理解すると、全体感がつかめるようになります。
その3種類の力とは以下のとおりです。
上の3つのうち「軸力によって、緩む方向に滑ろうとする力」と「ねじ面で発生する摩擦力」はねじ面で、「座面で発生する摩擦力」は座面で発生するので、締付けトルクは以下のように分けて考えることができます。
$$T=T_s+T_w$$
| $$T$$ | 締付けトルク |
| $$T_s$$ | ねじ面で必要な締付けトルク |
| $$T_w$$ | 座面で必要な締付けトルク |

ねじの力学では、ねじ頭が母材に接した状況についてを考えます。
それ以外の場合については、これから紹介する理論は適用外です。
例えば、ねじが締め切っておらずボルト・ナットの座面が母材に接していない状況については適用外で、そもそも中途半端なねじの締め付けでの使用は望ましくありません。
以下の記事でも解説しているとおり、機械を稼働させている間にどんどん緩みが進行して脱落してしまったり、ねじにかかる不可が大きすぎて破断したりしてしまいます。

ねじは応力集中の塊みたいなものなので、適切ではない使い方をするとすぐダメになってしまいます・・・
また、ねじ頭のない「止めねじ」や、固定用ではない「送りねじ」についても適用外です。
普通のねじとは発生する力が異なりますし、そもそも「部品の固定」という観点で言えば、通常のボルト・ナットの方が性能が高いです。
英単語がわからないと英文が読めないのと同様に、ある程度ねじの用語がわからないと読み進めるのが困難な場面があります。
ここでは、ねじの力学について読み進める上で知っておくべき用語をピックアップし、解説いたします。
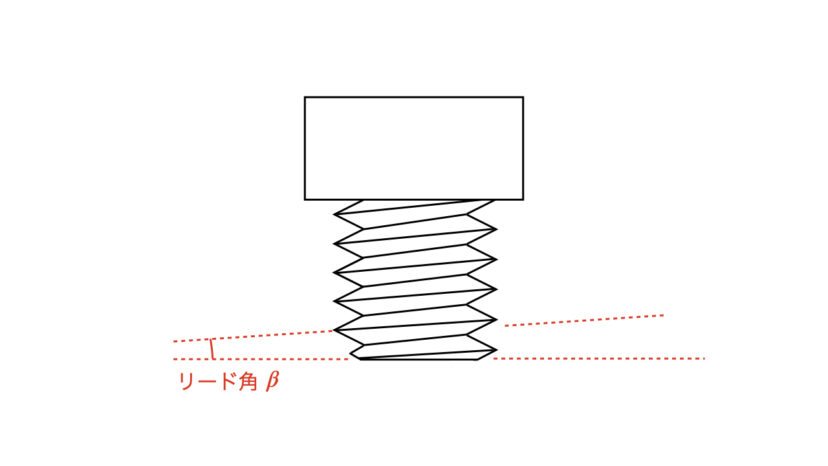
リード角とは、ねじの斜面の角度のことを言います。
日本で使われている固定用ねじは、リード角がおおよそ「2~4°」ぐらいで製造されています(M3・M4など、ねじのサイズによってバラバラです)。
ちなみに、リード角が大きいほどねじを回した際の進みが早い(スイスイ入っていく)ですが、その代わり緩みやすくなります。
逆にリード角が小さいほど緩みにくくなりますが、ねじを回しても進みが遅いです。
送りねじはリード角が大きく、固定用ねじはリード角が小さいのはそのためです。
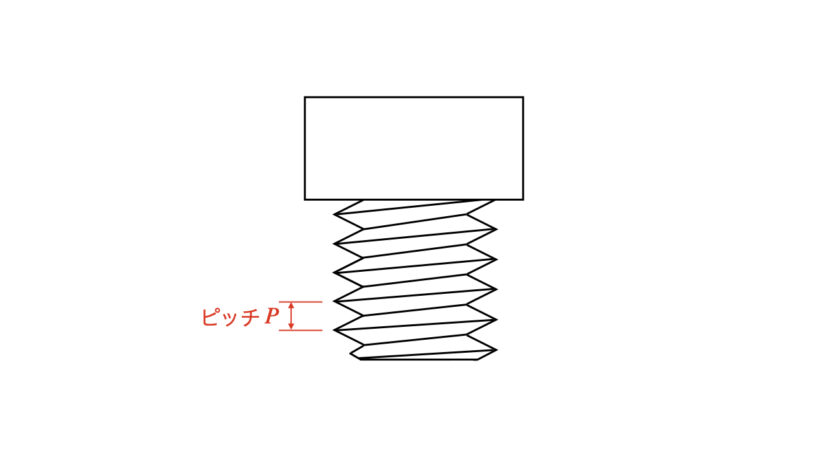
ねじのピッチとは、ねじの1山分の寸法のことを指します。
通常の並目ねじなどのような、世の中に多く普及しているねじは、ねじを1回転すると1ピッチ分だけねじ込まれていきます。
なお、普及率も、実際に使う場面も少ないですが、ねじを1回転させただけで2山、3山も進む「多条ねじ」や、並目ねじよりもピッチおよびリードが大きい「ハイリードねじ」というものもあります。
ねじの博士になりたい人は覚えておくといいでしょう。
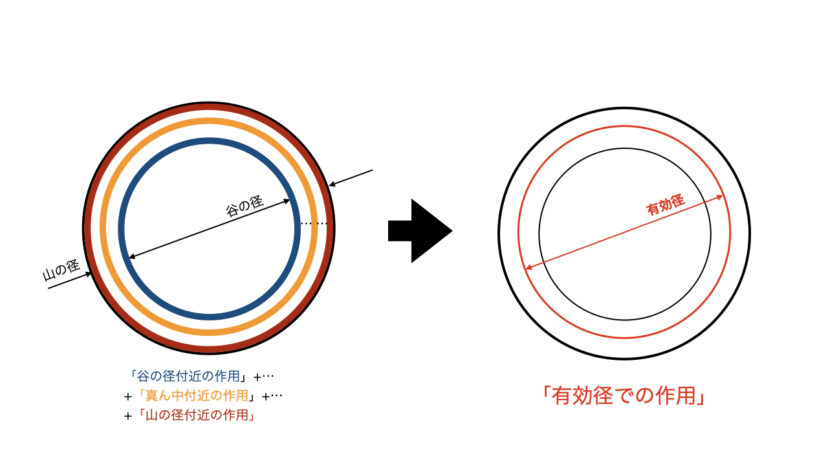
有効径とは、ねじの溝幅と、ねじの山幅とが同じになるような仮想的な円筒の直径のことを指します。
有効径は、以下の式で定義されますが、式自体は覚えなくてもいいです。
$$d_2=d-0.6495P$$
| $$d_2$$ | 有効径 |
| $$d$$ | ねじの呼び(おねじの山の径) |
| $$P$$ | ねじのピッチ |
実際にねじの嵌め合いは、おねじとめねじの面同士が接して締め付け力が発生します。
正攻法で計算しようとすると、「ねじの谷付近の作用」+…+「ねじの真ん中付近の作用」+…+「ねじの山付近の作用」といったように「一箇所ずつピンポイントで作用を考えて、全てを足し合わせる」といったことが必要になります。
これでは計算が非常に複雑になってしまいます。
そこで計算を簡単化するために「有効径の位置に全てが作用するもの」として考えることで、厳密な値とだいたい同じになります。
有効径に使われている数値はなんだかよくわからないものになっていますが、「厳密な値とだいたい近しい値にするために中途半端な数字になっている」という程度に認識してもらえればOKです。
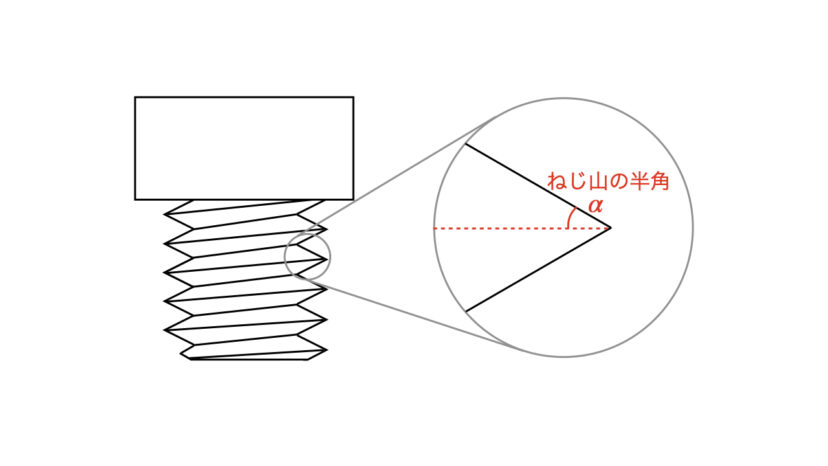
その名の通り、ねじ山の角度の半分のことを指します。
JIS規格の一般的なボルト・ナットのねじ山は正三角形で60°の形をしているため、ねじ山の半角は30°となります。
記号は、αがよく使われます(2α=60°、α=30°)。
摩擦係数といえば「μ」がおなじみかと思いますが、それではなく摩擦を角度で表記した「摩擦角」というものを使用していきます。
「摩擦なのに角度?」といったように、最初は慣れないかもしれませんが難しく考える必要はなく、何度か見ていくうちに慣れていきます。
摩擦係数と摩擦角とは、以下のような関係があります。
$$\tan\rho=\mu$$
| $$\rho$$ | 摩擦角 |
| $$\mu$$ | 静止摩擦係数 |
単に摩擦係数を別の表現(角度)にしただけであって、ねじのどこかの角度を表しているわけではないので注意してください。
主に、おねじとめねじの嵌め合い部の摩擦を考える際に、使用していきます。
一方的に「摩擦角とはそういうものだ」と言われても納得ができない方のために、証明をしておきます。
特に難しい要素はなく、高校物理の力学を少しかじってさえいれば簡単にできるので安心してください。
以下の図のように、斜面に乗った物体が静止している状況を考えます。

| $$m$$ | 物体の質量 |
| $$g$$ | 重力加速度 |
| $$\rho$$ | 斜面の角度 |
| $$\mu$$ | 静止摩擦係数 |
この物体について、釣り合いの式を立てていきます。
x軸方向、y軸方向についての釣り合いと、摩擦力の定義より、
$$\begin{cases}
f_0-mg\sin\rho=0 \cdots(1)&\\
N-mg\cos\theta=0 \cdots(2)&\\
f_0=\mu N \cdots(3)&
\end{cases}$$
| $$f_0$$ | 静止摩擦力 |
| $$N$$ | 垂直抗力 |
(3)式をNについて整理し、(2)式に代入すると、
$$f_0-\mu mg\cos\theta=0$$
これをf0について整理し、(1)式に代入すると
$$\mu mg\cos\theta-mg\sin\theta=0$$
$$\mu=\tan\theta$$
となり、証明完了です。
今回の内容についてまとめると、以下の通りとなります。
次回は、ねじ面の力関係について解説していきます。
ご一読、ありがとうございました。
ねじ関連のおすすめ書籍▼
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

ボルトの座面は斜めや曲面にするべきではない理由
【解説】締め付けトルクと軸力の関係式の導出(2)