材料力学 演習問題 02【棒の応力とひずみ】

今回は演習問題を作成いたしました。

問題は全部で3問あります。

下の方に解答を載せておりますので、答え合わせにご使用ください。

なお、この演習問題では、以下の内容が前提となっております。

• 材料が均質体である
• 等方性材料である
• 材料が連続体である
• 仮想断面上で発生する内力は一様である
• 断面積変化を無視する

問題

問1

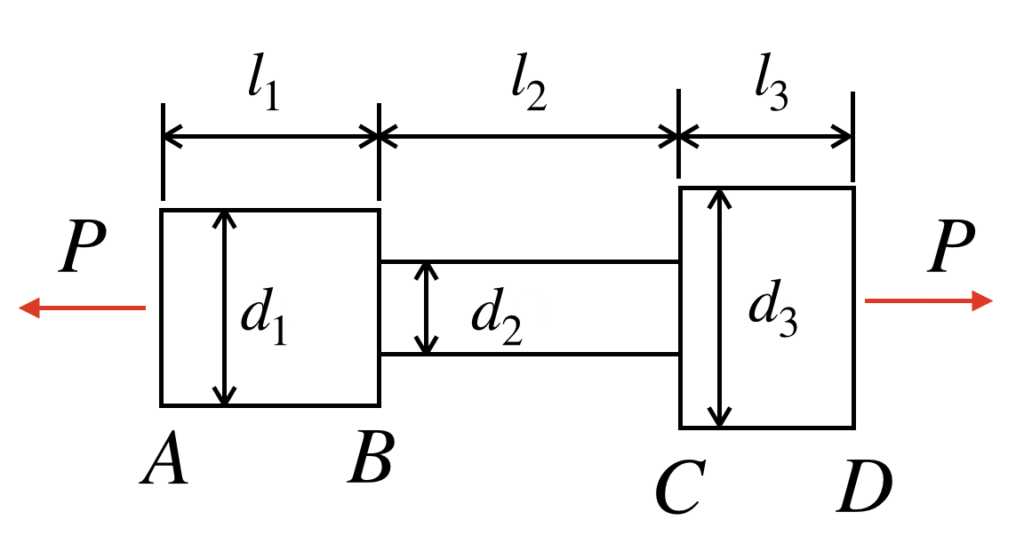
AB間の直径d₁　長さl₁、BC間の直径がd₂　長さl₂、CD間の直径がd₃　長さl₃である段付き棒の両端を、荷重Pで引張ります。この時の段付き棒全体のひずみ量を求めてください。

ここでd₁=40mm、d₂=20mm、d₃=50mm、l₁=50mm、l₂=80mm、l₃=40mm、ヤング率は206,000MPa、P=30,000Nとします。なお、応力とひずみは常に比例関係を保つとし、材料に発生する応力は、各区間で一様とします。

答え

問2

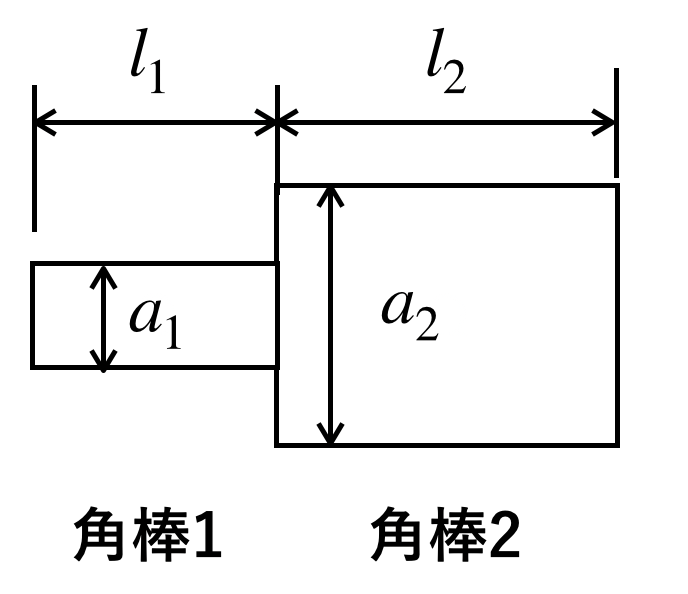
長さl₁で、一辺の長さがa₁で断面が正方形である角棒1と、長さl₂で、一辺の長さがa₂で断面が正方形である角棒2がお互いの端面で固定されております。

この棒を、全体的にΔlだけ引張って伸ばしました。

このとき、角棒1、角棒2それぞれに発生する応力を求めてください。

ただし、a₁=20mm、a₂=50mm、l₁=100mm、l₂=50mm、Δl=5mm、ヤング率を70,600N/mm^2とします。なお、応力とひずみは常に比例関係を保つとし、材料に発生する応力は、各材料内で一様とします。

答え

問3

ここに直径d、重量Wの丸棒があります。この丸棒を水平に置いた時の長さはL₁でした。また、棒の端を天井にぶら下げた時の棒の長さはL₂でした。このとき、棒のヤング率Eを求めてください。ここで、重力加速度はgとします。なお、応力とひずみは常に比例関係を保つとします。

答え

答え

問1

棒は引張荷重と同じ方向にひずみが発生することが考えられます。

ひずみをどのように求めるかですが、今回の問題では「変形後の寸法」や「変形量（伸びの量）」はわかりません。

そのため、応力を求めた後、フックの法則を使って求めるという方針で計算しましょう。

そのために、各区間において、仮想的に切り離し、計算を進めていきます。

区間ABについて、内力をF_AB、発生する応力をσ_AB、発生するひずみをε_ABとすると、

$$\begin{array}{rl}{F}_{AB}& =P\\ {\sigma }_{AB}& =\frac{F_{AB}}{\pi d_1^2/4}=\frac{P}{\pi d_1^2/4}\\ {\epsilon }_{AB}& =\frac{{\sigma }_{AB}}{E}=\frac{P}{\pi d_1^2/4\cdot E}\end{array}$$

区間BC、区間CDについても同様に

$$\begin{array}{rl}{F}_{BC}& =P\\ {\sigma }_{BC}& =\frac{F_{BC}}{\pi d_2^2/4}=\frac{P}{\pi d_2^2/4}\\ {\epsilon }_{BC}& =\frac{{\sigma }_{BC}}{E}=\frac{P}{\pi d_2^2/4\cdot E}\end{array}$$

$$\begin{array}{rl}{F}_{CD}& =P\\ {\sigma }_{CD}& =\frac{F_{CD}}{\pi d_3^2/4}=\frac{P}{\pi d_3^2/4}\\ {\epsilon }_{CD}& =\frac{{\sigma }_{CD}}{E}=\frac{P}{\pi d_3^2/4\cdot E}\end{array}$$

全体のひずみ量は、各区間のひずみ量の和で求めることができるので、

$$\begin{array}{rl}\epsilon & ={\epsilon }_{AB}+{\epsilon }_{BC}+{\epsilon }_{CD}\\ & =\frac{P}{\pi d_1^2/4\cdot E}+\frac{P}{\pi d_2^2/4\cdot E}+\frac{P}{\pi d_3^2/4\cdot E}\\ & =\frac{P}{\pi /4\cdot E}\cdot (\frac{1}{d_1^2}+\frac{1}{d_2^2}+\frac{1}{d_3^2})\\ & =\frac{30,000N}{\pi /4\cdot 206,000MPa}\cdot (\frac{1}{(40mm{)}^2}+\frac{1}{(20mm{)}^2}+\frac{1}{(50mm{)}^2})\\ & =6.5\times {10}^{-4}\end{array}$$

が答えとなります。

問2

まずは絵を描いて状況を整理しましょう。

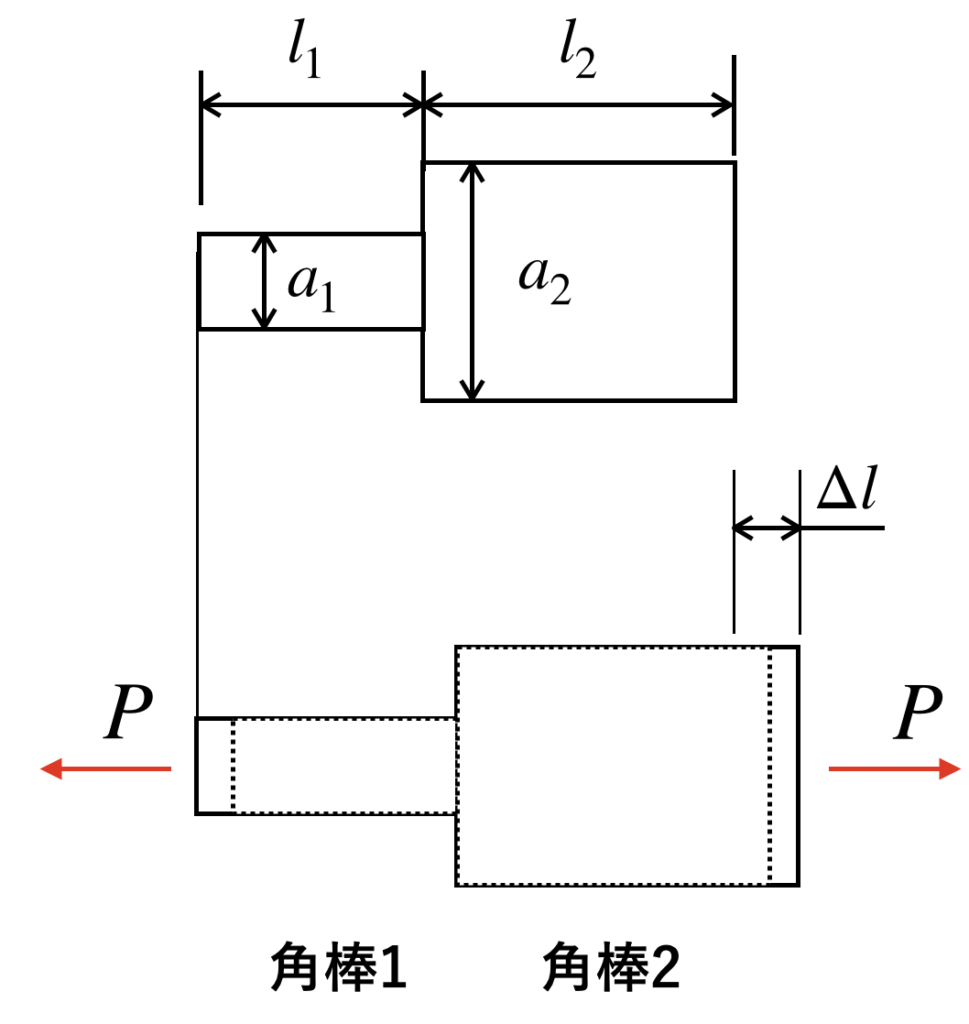
こういったように、まずは「どのような現象が起こっているか」を整理し、イメージをつかむことが大切です。

さて、計算をしたいのは各々の材料に発生する応力です。

ひずみ量を求めてフックの法則を使って計算をしたいところではありますが、肝心の個々のひずみ量がわかりません。

そのため、直接個々のひずみ量を求めるのは諦めて、棒全体にどのような現象が起こっているかに着目をして計算を進めていきましょう。

棒全体のひずみ量をεとすると、

$$\begin{array}{r}\epsilon =\frac{\Delta l}{l_1+l_2}\end{array}$$

また、外力をP、角棒1に発生する応力をσ1、角棒2に発生する応力をσ2とすると、各棒に発生する内力はPとなるので（式を省略します）、

$$\begin{array}{r}{\sigma }_1=\frac{P}{a_1^2}\\ {\sigma }_2=\frac{P}{a_2^2}\end{array}$$

またフックの法則より

$$\begin{array}{rl}{\sigma }_1+{\sigma }_2& =E\epsilon \\ \frac{P}{a_1^2}+\frac{P}{a_2^2}& =E\cdot \frac{\Delta l}{l_1+l_2}\\ P(\frac{1}{a_1^2}+\frac{1}{a_2^2})& =E\cdot \frac{\Delta l}{l_1+l_2}\\ P& =E\cdot \frac{\Delta l}{l_1+l_2}\cdot \frac{1}{(1/a_1^2)+(1/a_2^2)}\end{array}$$

よって、

$$\begin{array}{rl}{\sigma }_1& =\frac{P}{a_1^2}\\ & =E\cdot \frac{\Delta l}{l_1+l_2}\cdot \frac{1}{(1/a_1^2)+(1/a_2^2)}\cdot \frac{1}{a_1^2}\\ & =E\cdot \frac{\Delta l}{l_1+l_2}\cdot \frac{1}{1+(a_1^2/a_2^2)}\\ & =70600N/m{m}^2\cdot \frac{5mm}{100mm+50mm}\cdot \frac{1}{1+((20mm{)}^2/(50mm{)}^2)}\\ & =2.0\times {10}^{3}N/m{m}^2\end{array}$$

$$\begin{array}{rl}{\sigma }_2& =\frac{P}{a_2^2}\\ & =E\cdot \frac{\Delta l}{l_1+l_2}\cdot \frac{1}{(1/a_1^2)+(1/a_2^2)}\cdot \frac{1}{a_2^2}\\ & =E\cdot \frac{\Delta l}{l_1+l_2}\cdot \frac{1}{(a_2^2/a_1^2)+1}\\ & =70600N/m{m}^2\cdot \frac{5mm}{100mm+50mm}\cdot \frac{1}{((50mm{)}^2/(20mm{)}^2)+1}\\ & =3.2\times {10}^{2}N/m{m}^2\end{array}$$

が答えとなります。

問3

まずは絵を描いて状況を整理します。

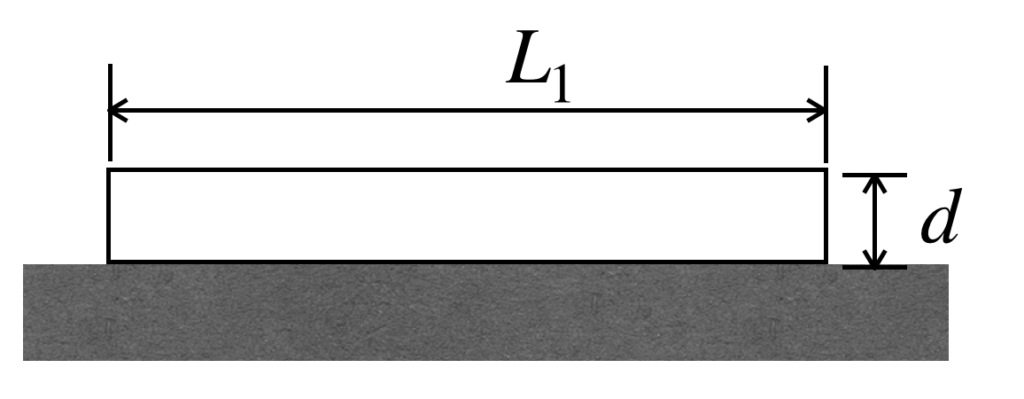
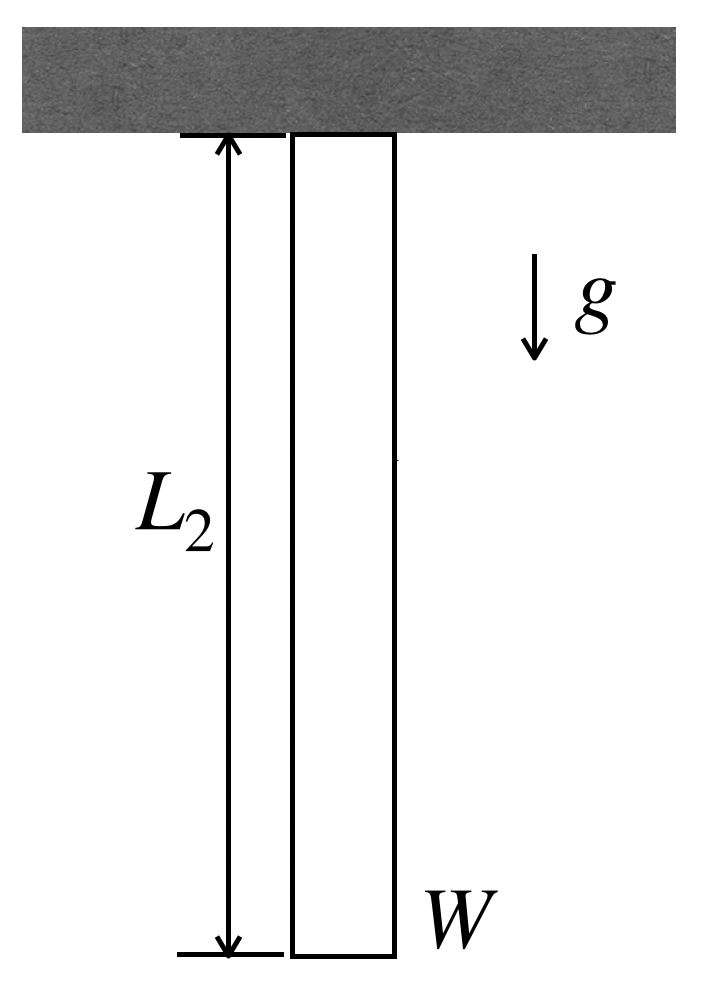
ヤング率を求めるには、フックの法則より

$$\begin{array}{r}E=\frac{\sigma }{\epsilon }\end{array}$$

を使います。（σ：応力、ε：ひずみ）

まず応力から求めてきます。

材料が天井に固定されている場合における外力は、天井からの反力です。

また、天井からの反力は、材料に働く重力と釣り合っています。よって、天井からの反力をRと、材料を仮想的に切り離し、内力をFとすると、

$$\begin{array}{r}F-R=0\\ Wg-R=0\end{array}$$

よって

$$\begin{array}{r}F=Wg\end{array}$$

応力を計算すると、

$$\begin{align\sigma&=\frac{F}{\pi d^2/4}\
&=\frac{Wg}{\pi d^2/4}
\end{align}$$

続いてひずみを計算すると

$$\begin{array}{r}\epsilon =\frac{L_2-L_1}{l_1}\end{array}$$

よってヤング率は

$$\begin{array}{rl}E& =\frac{\sigma }{\epsilon }\\ & =\frac{Wg}{\pi d^2/4}\cdot \frac{L_1}{L_2-L_1}\end{array}$$

これが答えです。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...