高校生でも理解できる！静止摩擦係数の測定原理

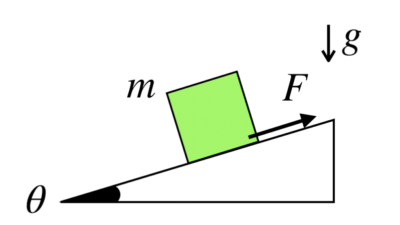
今回は、静止摩擦係数の測定原理についてお話しします。

静止摩擦係数は、対象とする物体の材質が同じであっても、温度や接触面の粗さなど、物体が置かれている材質が置かれている状況が異なるだけで、値がばらつきます。

そこで以前、机の上でも簡単に測定ができる方法についてお話ししました。

机でできる！　静止摩擦係数の測定方法

今回は、静止摩擦係数の簡単な測定についてお話しします。 何か設計をする際に静止摩擦係数を知りたくなることがしばしばありますが、基本的にデータはグーグルで検索をしても見つかりません。 それは、静止摩擦係…

ものづくりのススメ

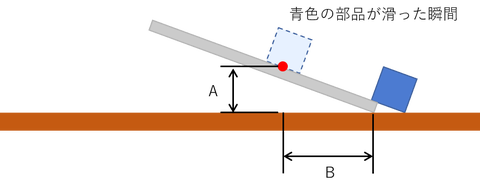
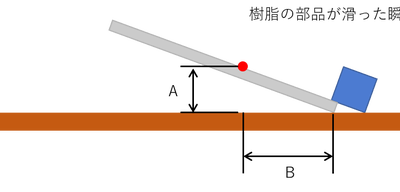
結論を言うと、以下の図の「グレー」と「青色」の部品との静止摩擦係数は
以下の図のAとBの長さを測り、A/BをすればOKです。

[mathjax]
$$\mu=\frac{A}{B}$$

その原理は、高校生で習う物理の知識があれば、十分理解することができます。
その理由をご説明いたします。

まずは、以下の図をご覧ください。

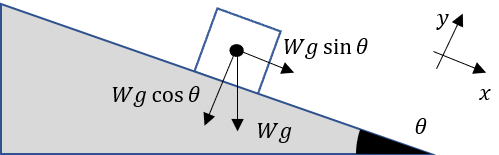
Wは白い物体の質量、gは重力加速度、θは傾斜角を表しています。

ここで、白い物体が静止しているとします。
上の図に、さらに「白い物体」が「灰色の斜面」から受ける力を書き足してみます。

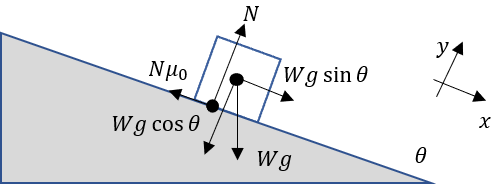
Nは灰色の部品から受ける「垂直抗力」、μ_0は「静止摩擦係数」です。

ではつり合いの式を立てます。

x軸方向について、力のつり合いを考えると以下のようになります。

[mathjax]
$$N-Wgcos\theta=0・・・(1)$$

続いて、y軸方向について力のつり合いを考えると以下のようになります。

[mathjax]
$$N\mu_0-Wgsin\theta=0・・・(2)$$

(1)と(2)を使ってNを消去すると、

[mathjax]
$$\mu_{0}Wgcos\theta-Wgsin\theta=0$$

[mathjax]
$$\mu_0=\frac{sin\theta}{cos\theta}=tan\theta$$

となります。

そのため、白い物体が静止する最大の傾斜角をθ’とすると

[mathjax]
$$\mu=tan\theta’$$

μは、静止摩擦係数です。

tanθ’は、白い物体が動いた瞬間のAとBの長さを測り、A/Bを計算することで、求めることができます。

手ごろに測定できますので、知っておくととても便利です。

ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり

機械設計のご依頼も承っております。こちらからお気軽にご相談ください。

構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...